A semi-circular ring has mass m and radius R as shown in figure. Let I1,I2,I3 and I4 be the moments of inertia about the four axes as shown . Axis 1 passes through centre and is perpendicular to plane of ring. Then , match the following.
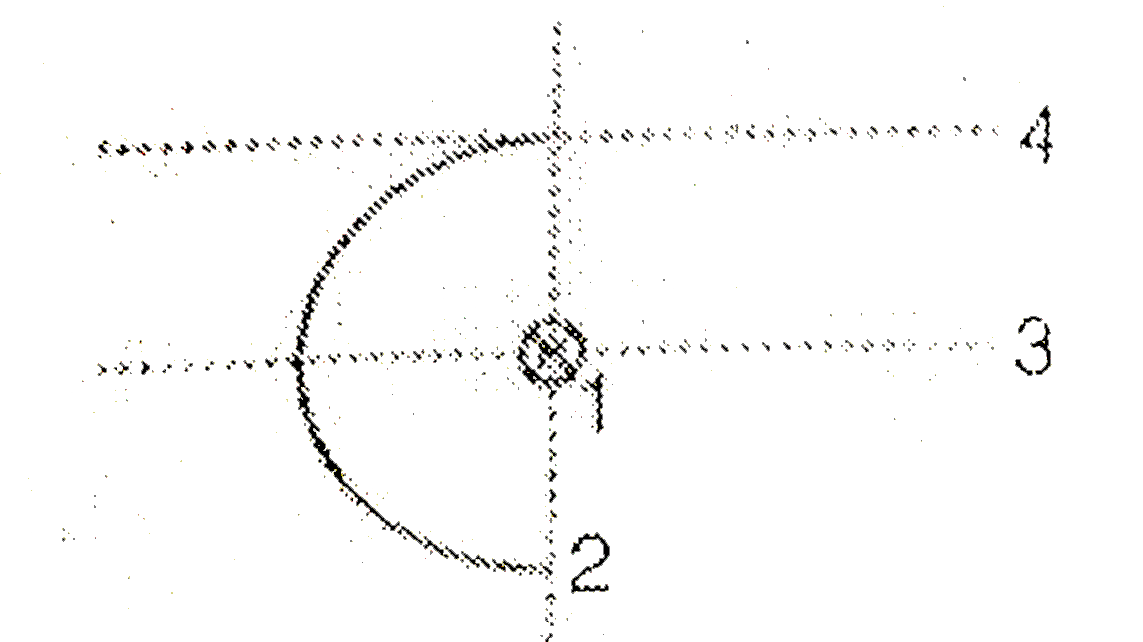

The correct Answer is:(A→r,B→p,C→p,D→q)
Moment of inertia of a ring about an axis perpendicular and passing through the centre of ring is MR2. Moment of inertia of a ring about diameter is MR2/2. From parallel axes theorem,
I4=MR22+MR2=32MR2.
Topper's Solved these Questions
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(A) Chapter Exercises
Explore 83 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Integer type q.
Explore 14 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
Similar Questions
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThe moment of inertia of a circular ring of mass 1 kg about an axis passing through its centre and perpendicular to its plane is 4 kg m2. The diameter of the ring is
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
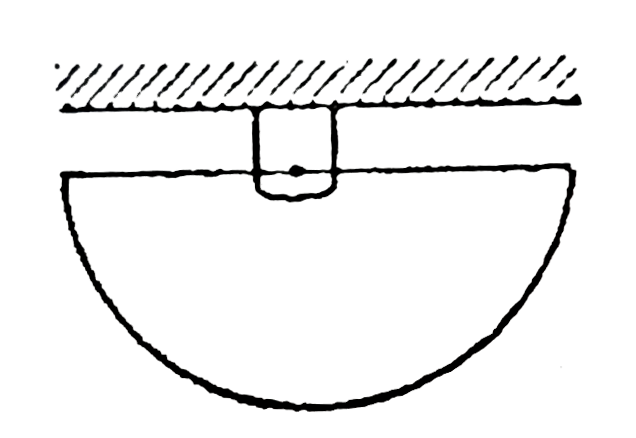
View SolutionA uniform semi-circular disc of mass m and radius r is suspended as shown in the figure. If T is the time period of small osciallations about an axis passing through point of supension and perpendicular to plane of disk. Then T is equal to
View SolutionFrom a complete ring of mass M and radius R, a 30∘sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,
,
View Solution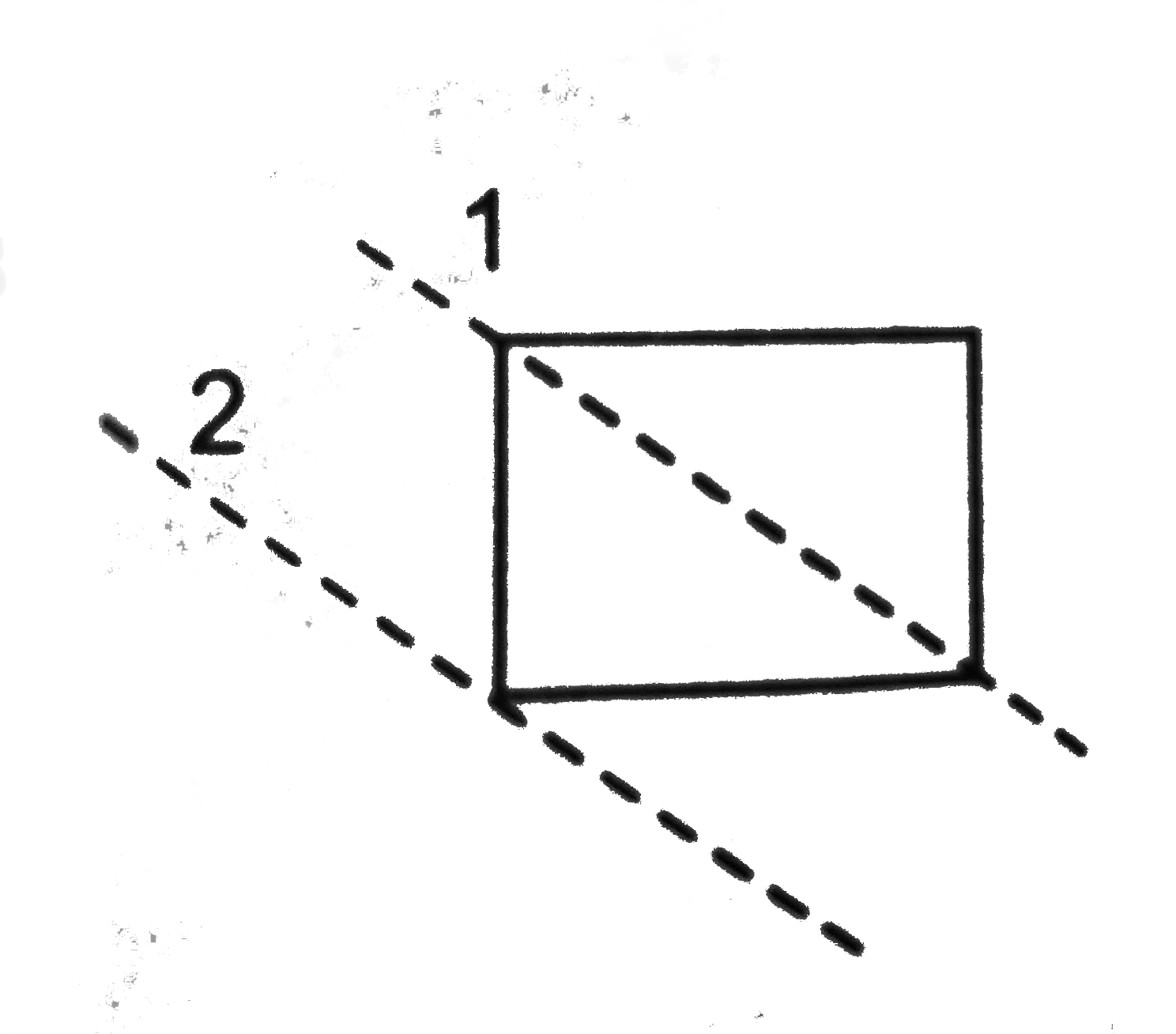
Let I1 and I2 be the moment of inertia of a uniform square plate about axes shown in the figure. Then the ratio I1:I2 is
View SolutionLet IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not. Then
View SolutionA uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
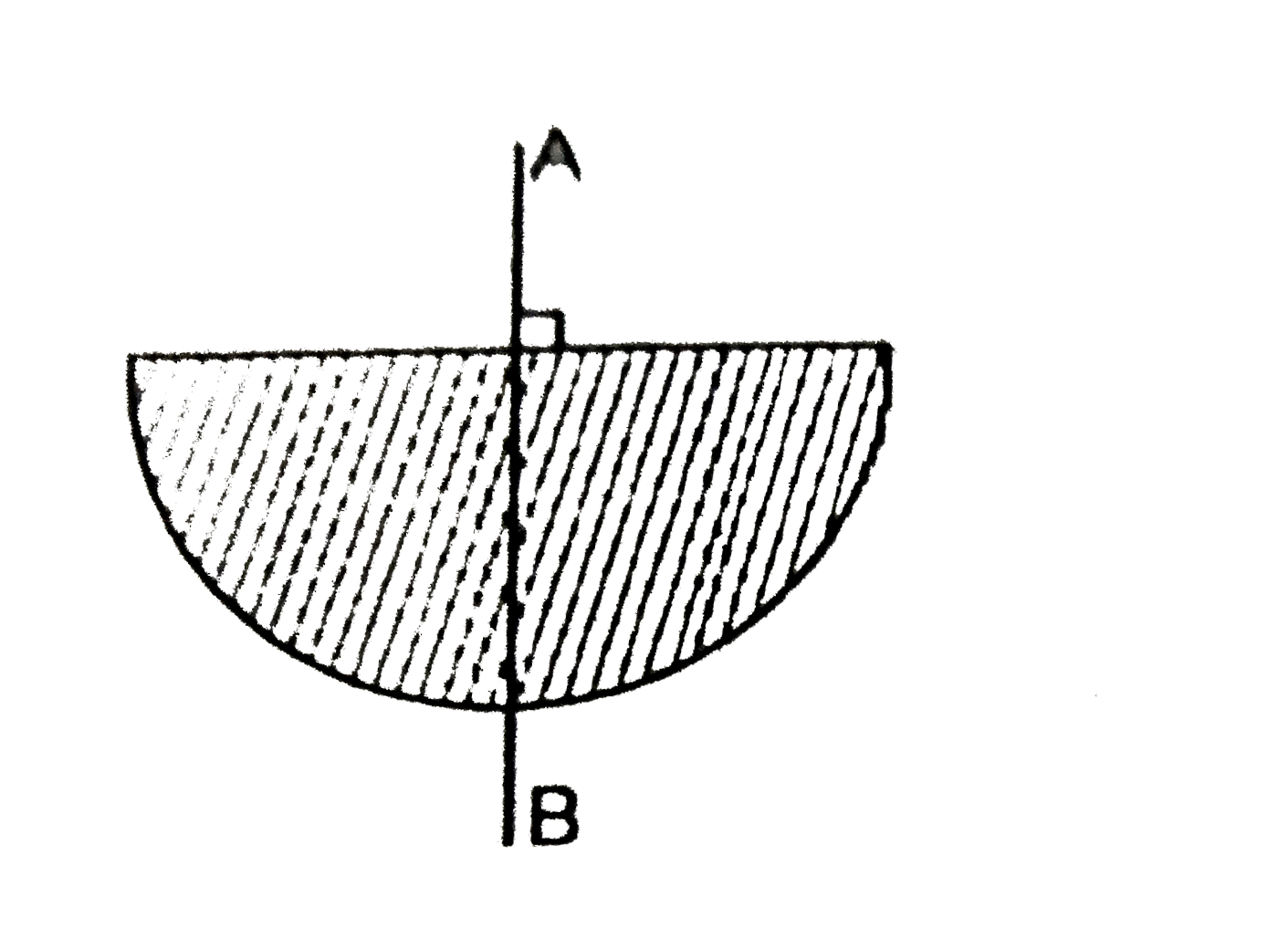
View SolutionThree rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.

View Solution