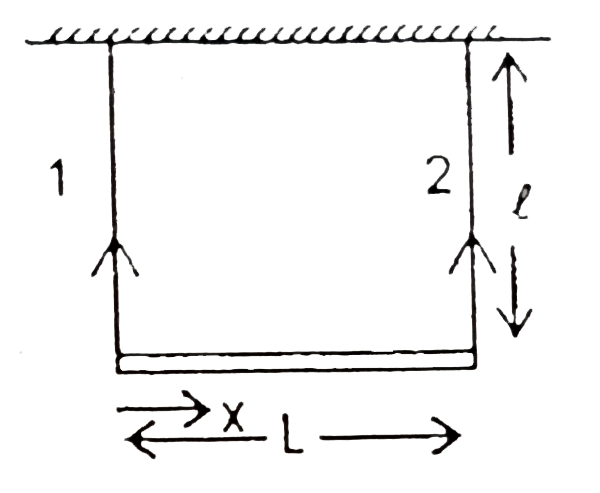
Assertion : Two strins shown in figure have the same tension. Speed of transverse waves in string−1 will be more.
 Reason : v∝1√μ,Heremu is mass per unit length of string.
Reason : v∝1√μ,Heremu is mass per unit length of string.
If both Assertion and Reason are true and the Reason is correct expanation of the Assertion.
If both Assertion and Reason are true but the Reason is not correct expanation of the Assertion.
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:D
Just by observation we cannot say that μ2>μ1 and hence v2>v1.
If their densities are different, then μ2 may be less then μ1 also.
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Objective Questions
1 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Level 1 Objective
6 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Exercise 17.6
6 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
Velocity of transverse waves in strings is given by the formula V=√Tμ, where and μ are respectively
View SolutionDerive an expression for the velocity of pulse in a in stretched in string under a tension T and μ is the mass per unit length of the sting.
View SolutionAssertion : Two resistance wires shown in figure are of same material. They have equal length. More heat is generated in wire A.

Reason : In series H∝R and resistance of wire A is more.
View SolutionA 660 Hz tuning fork sets up vibration in a string clamped at both ends. The wave speed for a transverse wave on this string is 220ms−1 and the string vibrates in three loops. (a) Find the length of the string. (b) If the maximum amplitude of a particle is 0.5 cm, write a suitable equation describing the motion.
View SolutionTwo strings of the same length but different mass per unit length are used to suspend a rod whose density varies as ρ=ρ0[1+αx] as shown in the figure. The frequency of standing waves produced in the string is in the ratio n:1, when both the strings are vibrating in their fundamental mode. If the mass per unit length of string (l) is μ0, calculate the mass per unit length of the other string.
View SolutionA composition string is made up by joining two strings of different masses per unit length 1g/ m and 4 g/m. The composite string is under the same tension. A transverse wave pulse : Y = (6 mm) sin(5t + 40x), where it is in seconds and 'x' in meters, is sent along the lighter string towards the joint. The joint is at x = 0. The equation of the wave pulse reflected from the joint is
View SolutionCheck the accuracy of the relation v=12l√Tm,where v is the frequency, l is legth, T is tension and m is mass per unit legth of the string.
View SolutionBoth the strings, shown in figure, are made of same material and have same cross-section. The pulleys are light. The wave speed of transverse wave in the string AB is v1 and in CD it is v2, the v1/v2 is

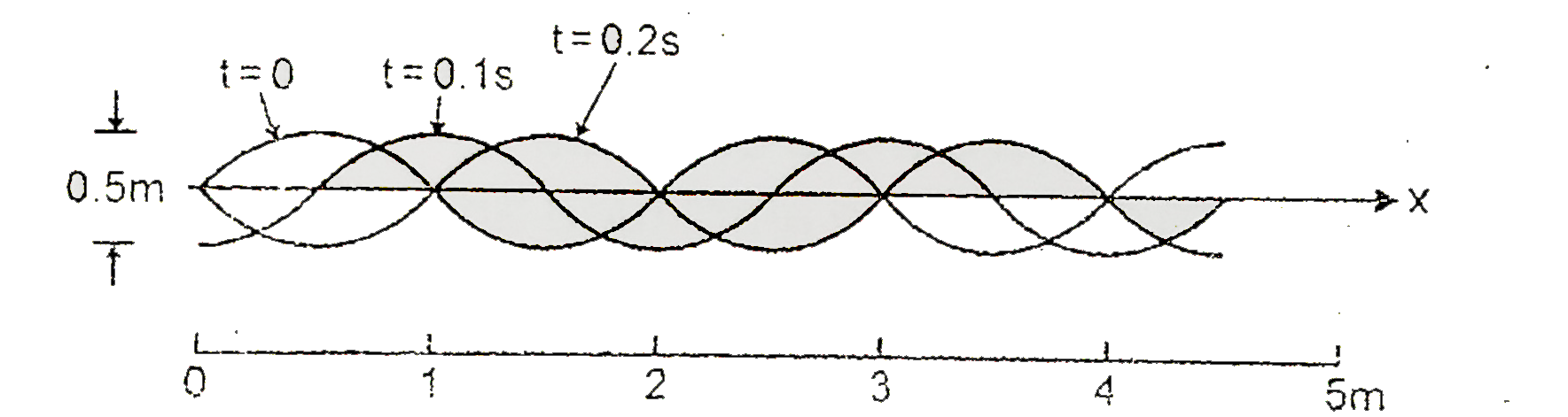
View SolutionThree consecutive flash photographs of a travelling wave on a string wave on a string are reproduced in the figure here. The following oberservation are made. Mark the one which is correct. (Mass per unit length of the sting =3g/cm.)
View SolutionThe extension in a string obeying Hooke's law is x. The speed of transverse wave in the stretched string is v. If the extension in the string is increased to 1.5x, the speed of transverse wave will be
View Solution
