Derive an expression for the velocity of pulse in a in stretched in string under a tension T and μ is the mass per unit length of the sting.
The correct Answer is:The broad view of the pulse under the tension T is given by
(##RESWFPMPHYXIC05E01014_A01##)
As; 2Tsin(θ)2=dmv2R
⇒2Tθ2=(ml).Rθ(v2))R
⇒v=√Tμ
where μ=ml, is the mass per unit length of the string also known as the linear mass density.
To derive the expression for the velocity of a pulse in a stretched string under tension T with mass per unit length μ, we can follow these steps:
Step 1: Understand the relationship between tension, mass, and velocity
The velocity of a wave on a string is influenced by the tension in the string and the mass per unit length. The basic relationship we want to derive involves these two quantities.
Step 2: Consider the forces acting on a small segment of the string
When a pulse travels along the string, consider a small segment of the string. The tension T acts on both ends of this segment. The net force acting on this segment can be analyzed using Newton's second law.
Step 3: Set up the equation of motion
For a small segment of the string, the net upward force due to tension can be expressed as:
F=Tsin(θ1)−Tsin(θ2)
where θ1 and θ2 are the angles the string makes with the horizontal at the ends of the segment.
Step 4: Use the small angle approximation
For small angles, we can use the approximation sin(θ)≈θ. Thus, we can rewrite the force as:
F≈Tθ1−Tθ2
Step 5: Relate the angles to the displacement
Assuming the segment has a length Δx and a small vertical displacement y, we can relate the angles to the displacement:
θ1≈y1Δx,θ2≈y2Δx
where y1 and y2 are the vertical displacements at the two ends of the segment.
Step 6: Substitute the angles into the force equation
Substituting the expressions for θ1 and θ2 into the force equation gives:
F≈T(y1−y2Δx)
Step 7: Apply Newton’s second law
According to Newton's second law, the net force is also equal to mass times acceleration. The mass of the segment is μΔx, and the acceleration can be expressed as ∂2y∂t2:
F=μΔx∂2y∂t2
Step 8: Equate the forces
Setting the expressions for force equal gives:
T(y1−y2Δx)=μΔx∂2y∂t2
Step 9: Rearranging the equation
Rearranging this equation leads to:
Tμ=∂2y∂t21Δx
Step 10: Identify the wave velocity
Recognizing that the wave velocity v is defined as:
v=√Tμ
This is the expression for the velocity of a pulse in a stretched string under tension T and mass per unit length μ.
Final Expression
Thus, the final expression for the velocity of a pulse in a stretched string is:
v=√Tμ
The velocity of a wave on a string is influenced by the tension in the string and the mass per unit length. The basic relationship we want to derive involves these two quantities.
When a pulse travels along the string, consider a small segment of the string. The tension T acts on both ends of this segment. The net force acting on this segment can be analyzed using Newton's second law.
For a small segment of the string, the net upward force due to tension can be expressed as:
F=Tsin(θ1)−Tsin(θ2)
where θ1 and θ2 are the angles the string makes with the horizontal at the ends of the segment.
For small angles, we can use the approximation sin(θ)≈θ. Thus, we can rewrite the force as:
F≈Tθ1−Tθ2
Assuming the segment has a length Δx and a small vertical displacement y, we can relate the angles to the displacement:
θ1≈y1Δx,θ2≈y2Δx
where y1 and y2 are the vertical displacements at the two ends of the segment.
Substituting the expressions for θ1 and θ2 into the force equation gives:
F≈T(y1−y2Δx)
According to Newton's second law, the net force is also equal to mass times acceleration. The mass of the segment is μΔx, and the acceleration can be expressed as ∂2y∂t2:
F=μΔx∂2y∂t2
Setting the expressions for force equal gives:
T(y1−y2Δx)=μΔx∂2y∂t2
Rearranging this equation leads to:
Tμ=∂2y∂t21Δx
Recognizing that the wave velocity v is defined as:
v=√Tμ
This is the expression for the velocity of a pulse in a stretched string under tension T and mass per unit length μ.
Thus, the final expression for the velocity of a pulse in a stretched string is:
v=√Tμ
Topper's Solved these Questions
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 1 PART I
23 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 1 PART II
31 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Solved Miscellaneous Problems
7 Videos
- TRAVELLING WAVESBOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 3 PART I
19 Videos
- WAVE OPTICSBOOK - RESONANCE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Advanced Level Problems
8 Videos
Similar Questions
The frequency (f) of a stretched string depends upen the tension F (dimensions of form ) of the string and the mass per unit length mu of string .Derive the formula for frequency
View SolutionThe velocity of transverse wave in a string is v=√T/m where T is the tension in the string and m is the mass per unit length . If T=3.0kgf, the mass of string is 25g and length of the string isv=1.000m, then the percentage error in the measurement of velocity is
View SolutionThe frequency v of the stretched string may depend on (i) the length of the vibrating segment 1 (ii) the tension in the string and (iii) the mass per unit length m. Show that v∝1l√Fm.
View SolutionCheck the accuracy of the relation v=12l√Tm,where v is the frequency, l is legth, T is tension and m is mass per unit legth of the string.
View SolutionDerive the expression for the self inductance of a long solenoid of cross sectional area A and length l, having n turns per unit length.
View SolutionFour pieces of string of length L are joined end to end to make a long string of length 4L. The linear mass density of the strings are μ,4μ,9μand16μ, respectively. One end of the combined string is tied to a fixed support and a transverse wave has been generated at the other end having frequency f (ignore any reflection and absorption). string has been stretched under a tension F.

Find the ratio of wavelength of the wave on four string, starting from right hand side.
View SolutionIn each of the four situations of column-I , a stretched string or an organ pipe is given along with the required data. In case of strings the tension in string is T=102.4 N and the mass per unit length of string is 1g/m. Speed of sound in air is 320 m/s. Neglect end corrections.The frequencies of resonance are given in column-II.Match each situation in column-I with the possible resonance frequencies given in Column-II.
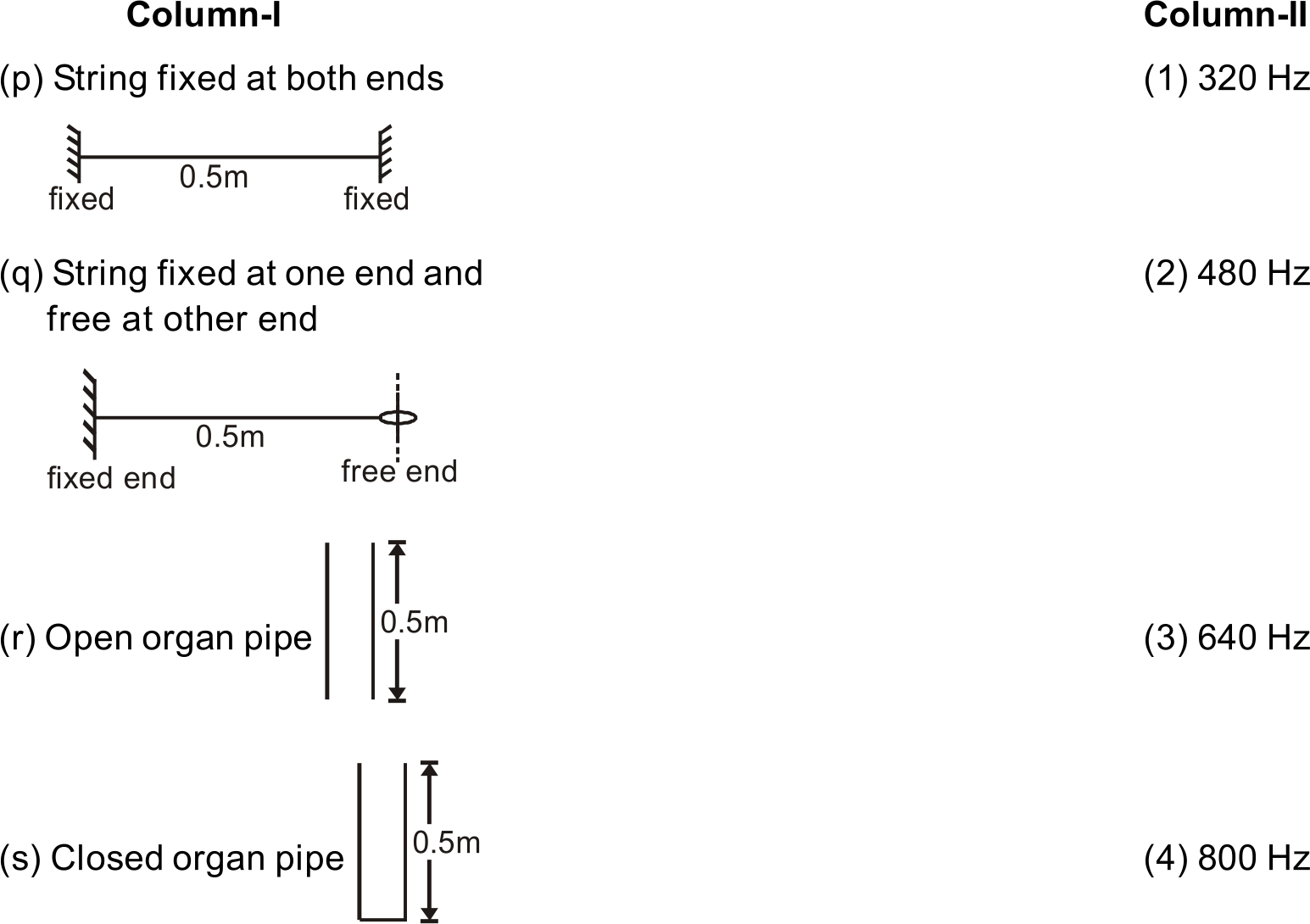
View SolutionThree strings of equal lengths but stretched with different tensions are inade to vibrate. If their masses per unit length are in the ratio 1:2:3 and the frequencies are the same, calculate the ratio of the tensions.
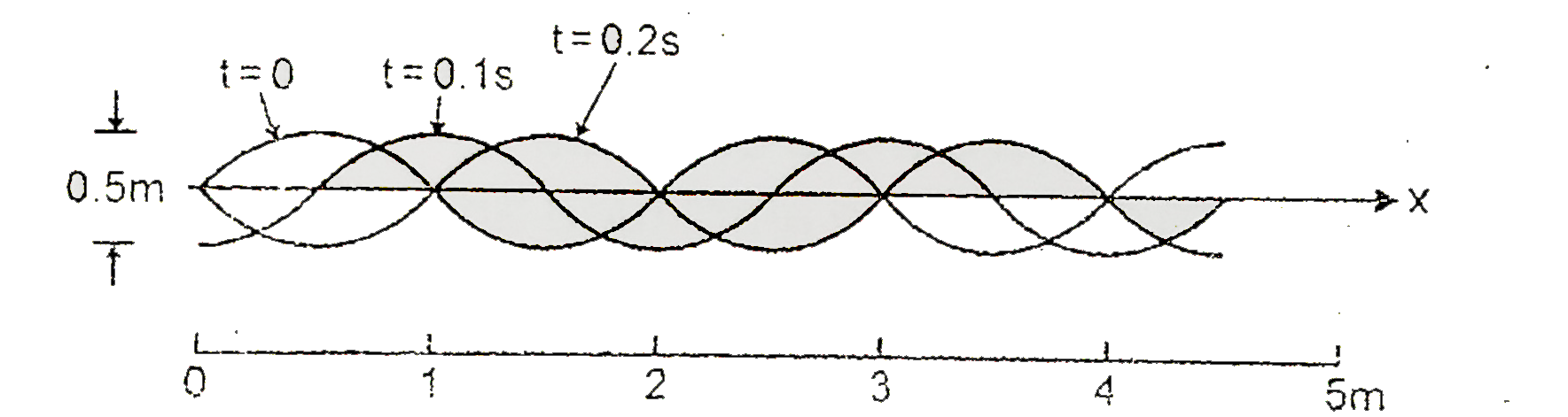
View SolutionThree consecutive flash photographs of a travelling wave on a string wave on a string are reproduced in the figure here. The following oberservation are made. Mark the one which is correct. (Mass per unit length of the sting =3g/cm.)
View SolutionAssertion : Two strins shown in figure have the same tension. Speed of transverse waves in string−1 will be more.
 Reason : v∝1√μ,Heremu is mass per unit length of string.
Reason : v∝1√μ,Heremu is mass per unit length of string.
View Solution
