Assume the dipole model of earth's magnetic field B which is given by BV= vertical component of magnetic field =μ04π2Mcosθr3, BH=Horizontal component of magnetic field =μ04πsinθMr3, θ=90∘-latitude as measured from magnetic equator.
Find loci of points for which dip angle is ±45∘.
tan−1(3)
tan−1(2)
tan−1(0.5)
tan−1(1)
The correct Answer is:B
To solve the problem, we need to find the loci of points where the dip angle is ±45°. The dip angle (also known as the angle of inclination) is defined as the angle made by the magnetic field with the horizontal plane.
1. Understanding the Dip Angle:
The dip angle θ is given by the relation:
tan(θ)=BVBH
where BV is the vertical component and BH is the horizontal component of the Earth's magnetic field.
2. Substituting the Components:
From the problem, we have:
BV=μ04π⋅2Mcosθr3
BH=μ04π⋅Msinθr3
3. Setting Up the Equation for ±45°:
For a dip angle of 45°:
tan(45°)=1
Thus, we can write:
BVBH=1
4. Equating the Components:
Substituting the expressions for BV and BH:
μ04π⋅2Mcosθr3μ04π⋅Msinθr3=1
The μ04π and 1r3 terms cancel out:
2McosθMsinθ=1
5. Simplifying the Equation:
Canceling M gives:
2cosθsinθ=1
Rearranging this, we have:
2cosθ=sinθ
6. Using Trigonometric Identity:
Dividing both sides by cosθ:
2=tanθ
7. Finding the Angle:
Therefore, we can find θ as:
θ=tan−1(2)
8. Considering ±45°:
Since we are interested in the loci for both +45° and −45°, we can conclude that the points where the dip angle is ±45° correspond to the latitude where θ=tan−1(2) and its symmetric counterpart.
Final Answer:
The loci of points for which the dip angle is ±45° corresponds to the latitude θ=tan−1(2).
The dip angle θ is given by the relation:
tan(θ)=BVBH
where BV is the vertical component and BH is the horizontal component of the Earth's magnetic field.
From the problem, we have:
BV=μ04π⋅2Mcosθr3
BH=μ04π⋅Msinθr3
For a dip angle of 45°:
tan(45°)=1
Thus, we can write:
BVBH=1
Substituting the expressions for BV and BH:
μ04π⋅2Mcosθr3μ04π⋅Msinθr3=1
The μ04π and 1r3 terms cancel out:
2McosθMsinθ=1
Canceling M gives:
2cosθsinθ=1
Rearranging this, we have:
2cosθ=sinθ
Dividing both sides by cosθ:
2=tanθ
Therefore, we can find θ as:
θ=tan−1(2)
Since we are interested in the loci for both +45° and −45°, we can conclude that the points where the dip angle is ±45° correspond to the latitude where θ=tan−1(2) and its symmetric counterpart.
The loci of points for which the dip angle is ±45° corresponds to the latitude θ=tan−1(2).
Topper's Solved these Questions
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - MAGNETISATION AND MAGNETIC INTENSITY
11 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - MAGNETIC PROPERTIES OF MATERIALS
26 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - MAGNETISM AND GAUSS S LAW
2 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Assertion And Reason
15 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Assume the dipole model of earth's magnetic field B which is given by BV= vertical component of magnetic field =μ04π2Mcosθr3, BH=Horizontal component of magnetic field =μ04πsinθMr3, θ=90∘-latitude as measured from magnetic equator.
Find loci of points for which (i) ∣∣→B∣∣ is minimum, (ii) dip angle is zero, and (iii) dip angle is ±45∘.
View SolutionThe vertical component of earth's magnetic field at a place is √3 times the horizontal component the value of angle of dip at this place is
View Solution
Knowledge Check
The vertical component of earth's magnetic field at a place is √3 times the horizontal component the value of angle of dip at this place is
A30∘B45∘C60∘D75∘
Calculate earth's magnetic field at a place where angle of dip δ is 60∘ and horizontal component of earth's magnetic field is 0.3 G
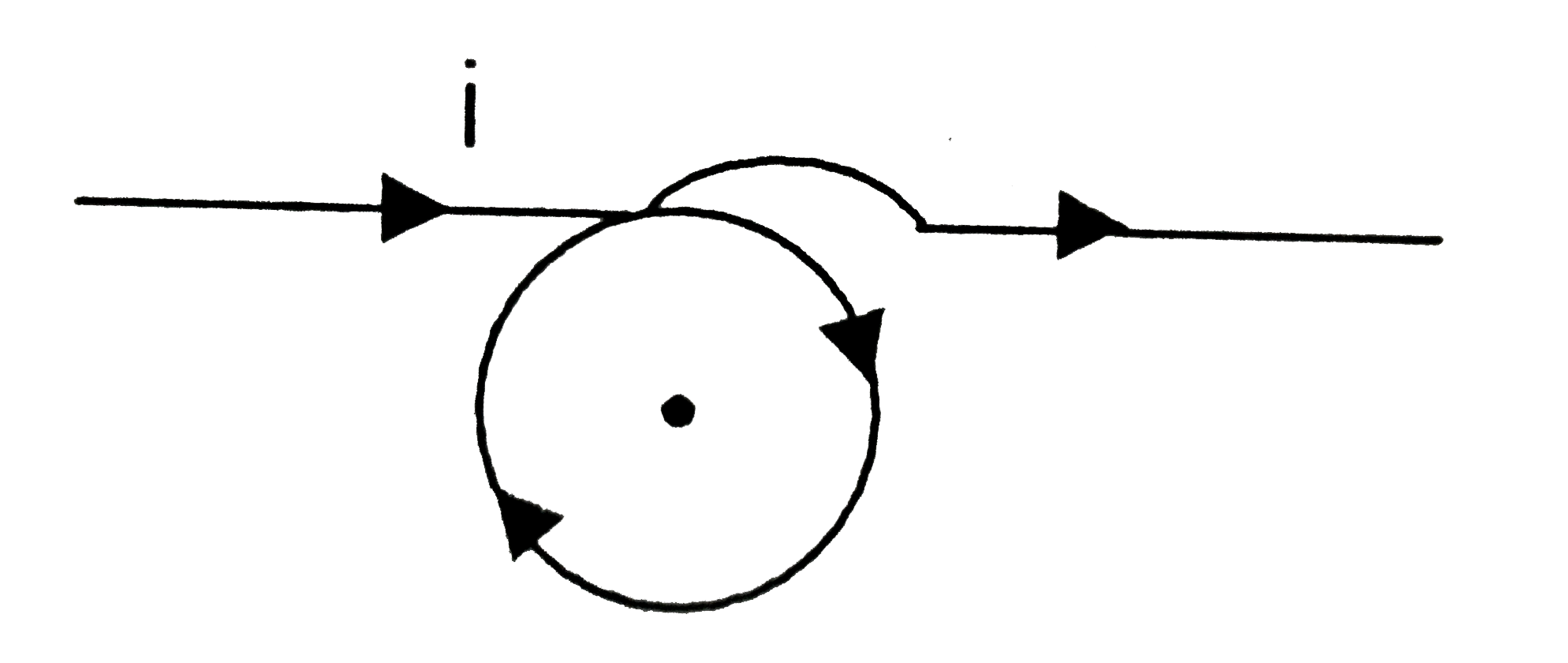
View SolutionIn the given figure find out magnetic field at point B (Given : I=2.5A, r=5cm)
View SolutionAt a place, the horizontal component of earth's magnetic field is V and angle of dip is 60∘. What is te value of horizontal component of earth's magnetic field at equator ?
View SolutionThe value of horizontal component of earth's magnetic field at a place is −.35×10−4T. If the angle of dip is 60∘, the value of vertical component of earth's magnetic field is about:
View SolutionThe horizontal component of earth.s magnetic field On at a place is 1√3 times the vertical component. Determine the angle of dip at that place.
View SolutionIn the magnetic meridian of a certain place, the horizontal component of earth's magnetic fied is 0.26G and the dip angle is 60∘. Find
a. Vertical component of earth's magnetic field
b. the net magnetic field at this place
View SolutionAt a place, the horizontal component of earth's magnetic field is B and angle of dip is 60∘. What is the value of horizontal component of earth's magnetic field at equator?
View Solution
