At a certain height a shell at rest explodes into two equal fragments. One of the fragments receives a horizontal velocity u. The time interval after which, the velocity vectors will be inclined at 120∘ to each other is
u√3g
√3ug
2u√3g
u2√3g
The correct Answer is:A
To solve the problem step by step, we will follow the principles of conservation of momentum and kinematics.
1. Understanding the Problem:
- A shell at rest explodes into two equal fragments.
- One fragment receives a horizontal velocity u.
- We need to find the time interval after which the velocity vectors of the two fragments are inclined at an angle of 120∘.
2. Initial Conditions:
- Before the explosion, the total momentum of the system is zero since the shell is at rest.
- After the explosion, let the first fragment (Fragment 1) have a velocity →v1=u^i+gt^j (moving horizontally with velocity u and falling under gravity).
- Let the second fragment (Fragment 2) have a velocity →v2=−u^i+gt^j (moving in the opposite horizontal direction and also falling under gravity).
3. Using the Cosine Rule:
- The angle between the two velocity vectors is given by the formula:
cosθ=→v1⋅→v2|→v1||→v2|
- We know that θ=120∘, thus cos120∘=−12.
4. Calculating the Dot Product:
- Calculate →v1⋅→v2:
→v1⋅→v2=(u^i+gt^j)⋅(−u^i+gt^j)=−u2+g2t2
5. Calculating the Magnitudes:
- The magnitude of →v1 and →v2:
|→v1|=|→v2|=√u2+(gt)2
6. Setting Up the Equation:
- Substitute into the cosine formula:
−12=−u2+g2t2u2+g2t2
7. Cross Multiplying:
- Rearranging gives:
−12(u2+g2t2)=−u2+g2t2
- This simplifies to:
−12u2−12g2t2=−u2+g2t2
8. Combining Like Terms:
- Rearranging terms:
12u2=32g2t2
9. Solving for Time t:
- Rearranging gives:
t2=u23g2
- Taking the square root:
t=u√3g
Final Answer:
Thus, the time interval after which the velocity vectors will be inclined at 120∘ to each other is:
t=u√3g
- A shell at rest explodes into two equal fragments.
- One fragment receives a horizontal velocity u.
- We need to find the time interval after which the velocity vectors of the two fragments are inclined at an angle of 120∘.
- Before the explosion, the total momentum of the system is zero since the shell is at rest.
- After the explosion, let the first fragment (Fragment 1) have a velocity →v1=u^i+gt^j (moving horizontally with velocity u and falling under gravity).
- Let the second fragment (Fragment 2) have a velocity →v2=−u^i+gt^j (moving in the opposite horizontal direction and also falling under gravity).
- The angle between the two velocity vectors is given by the formula:
cosθ=→v1⋅→v2|→v1||→v2|
- We know that θ=120∘, thus cos120∘=−12.
- Calculate →v1⋅→v2:
→v1⋅→v2=(u^i+gt^j)⋅(−u^i+gt^j)=−u2+g2t2
- The magnitude of →v1 and →v2:
|→v1|=|→v2|=√u2+(gt)2
- Substitute into the cosine formula:
−12=−u2+g2t2u2+g2t2
- Rearranging gives:
−12(u2+g2t2)=−u2+g2t2
- This simplifies to:
−12u2−12g2t2=−u2+g2t2
- Rearranging terms:
12u2=32g2t2
- Rearranging gives:
t2=u23g2
- Taking the square root:
t=u√3g
Thus, the time interval after which the velocity vectors will be inclined at 120∘ to each other is:
t=u√3g
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)
7 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (A boat in a river)
3 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - ADDITIONAL EXERCISE
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
Similar Questions
At a certain height a body at rest explodes into two equal fragments with one fragment receiving a horizontal velocity of 10ms^−1. The time interval after the explosion for which the velocity vectors of the two fragments become perpendicular to each other is
View SolutionAt a certain height a body at rest explodes into two equal fragments with one fragment receiving a horizontal velocity of 10ms−1. The time interval after the explosion for which the velocity vectors of the two fragments become perpendicular to each other is (g=10ms−2)
View SolutionA bomb at rest at the summit of a cliff breaks into two equal fragments. One of the fragments attains a horizontal velocity of 20√3ms−1. The horizontal distance between the two fragments, when their displacement vectors is inclined at 60∘ relative to each other is (g=10ms−2)
View SolutionAt high altitude , a body explodes at rest into two equal fragments with one fragment receiving horizontal velocity of 10m/s. Time taken by the two radius vectors connecting of explosion to fragments to make 90∘ is
View SolutionA particle of mass 4m which is at rest explodes into four equal fragments. All four fragments scattered in the same horizontal plane. Three fragments are found to move with velocity v as shown in the figure. The total energy released in the process is
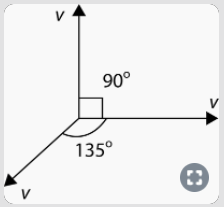
View SolutionA ball is projected with a velocity 20√3ms−1 at angle 60∘ to the horizontal. The time interval after which the velocity vector will make an angle 30∘ to the horizontal is (Take, g=10ms−2)
View SolutionA body is projected with a velocity u at an angle of 60∘ to the horizontal. The time interval after which it will be moving in a direction of 30∘ to the horizontal is
View SolutionA shell of mass 2kg moving at a rate of 4m/s suddenly explodes into two equal fragments. The fragments go in directions inclined with the original line of motion with equal velocities, If the explosion imparts 48J of translational kinetic energy to the fragments, find the velocity and direction of each fragment.
View SolutionA shell of mass 20kg at rest explodes into two fragments whose masses are in the ratio 2:3. The smaller fragment moves with a velocity of 6m/s. The kinetic energy of the larger fragment is
View SolutionA shell of mass 20kg at rest explodes into two fragments whose masses are in the ratio 2:3. The smaller fragment moves with a velocity of 6m/s. The kinetic energy of the larger fragment is
View Solution
