Question

At a place , the apparent geomagnetic dip in a vertical place is ${40}^{\circ }$ and in another plane perpendicular to it is ${30}^{\circ }$ .what is the real dip at the place ?
similar problem : If ${\theta }_1$ is the angle of dip of the magnetic axis of a magnetic needle with horizontal at any vertical plane and ${\theta }_2$ is that in another vertical plane at right former prove that real angle of dip , $\theta$ is given by ${\cot }^2\theta ={\cot }^2{\theta }_1+{\cot }^2{\theta }_2$.

Explanation

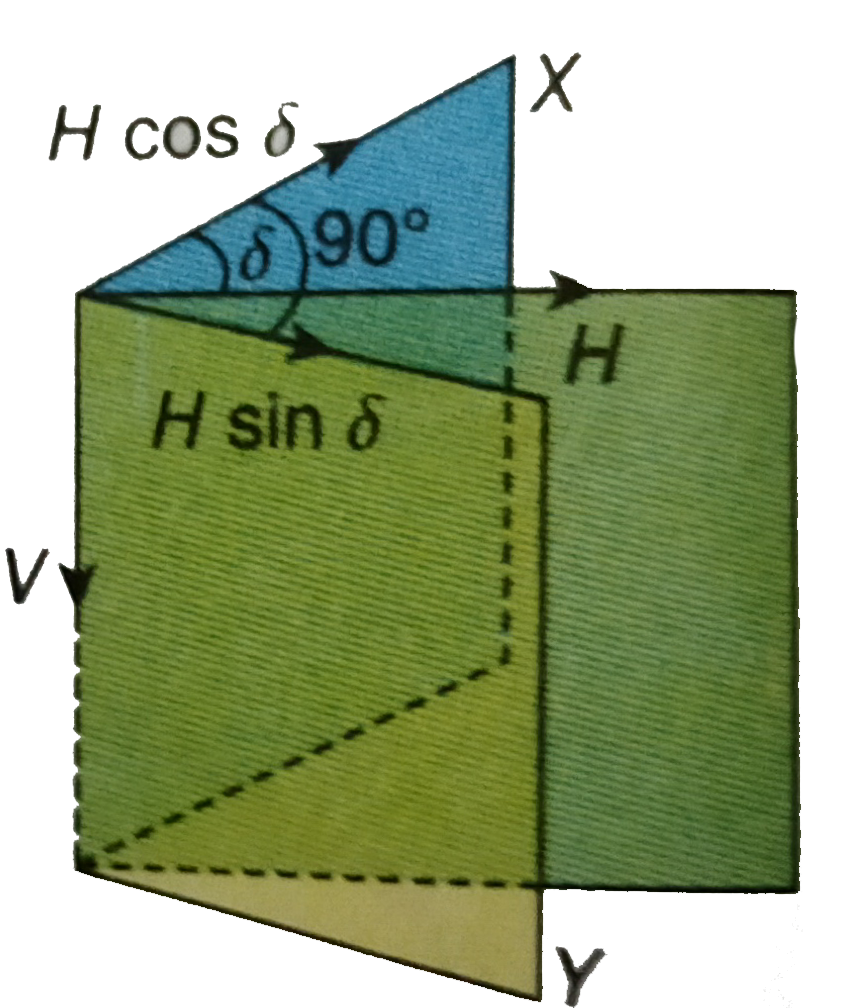
If the horizontal and vertical components of the earth's magnetic field are H and V , respectively and the true dip angle at the place is `theta` then ,
`tantheta=(V)/(H)" " ...(1)`
In Fig , M is the magnetic meridian and X , Y are two vertical planes inclined at right angle to each other .
The angle between the planes X and M is `delta` . If apparent dip in the plane X be `theta_(1)` then ,
`tantheta_(1)=(V)/(Hcosdelta) " "...(2)`
If the apparent dip in the plane Y be `theta_(2)` the, `tantheta_(2)=(V)/(Hsindelta)" "...(3)`
From equations (2) and (3) we det ,
`cot^(2)theta_(1)+cot^(2)theta_(2)=(H^(2))/(V^(2))(cos^(2)delta+sin^(2)delta)=(H^(2))/(V^(2))`
`cot^(2)theta` [from equation(1) ]
Here , `theta_(1)=40^(@)andtheta_(2)=30^(@)`
`therefore" " cot^(2)theta=cot^(2)40^(@)+cot^(2)30^(@)`
`"or, " cottheta=sqrt(1.42+3)=sqrt(4.42)=2.1`
`"or, " theta=cot^(-1)(2.1)=25.46^(@)`