At time t=t1, an object's velocity is given by the vector v1 shown below.

A short time later, at t=t2, the object's velocity is the vector v2

If v1andv2 have the same magnitude, which one of the following vectors best illustrates the object's average acceleration between t=t1andt=t2 ?
A

B

C

D

Text Solution
The correct Answer is:C
By definition, ¯a=Δv/Δt. We determine Δv=v2−v1=v2+(−v1) geometrically as follows :

Since Δt is a positive scalar the direction of ¯a is the same as the direction of Δv, which is displayed above, (c ) is best.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The graph shown the variation with times t of the velocity v of an object . Which one of the following graphs best represents the variation of acceleration a of the object with time t?
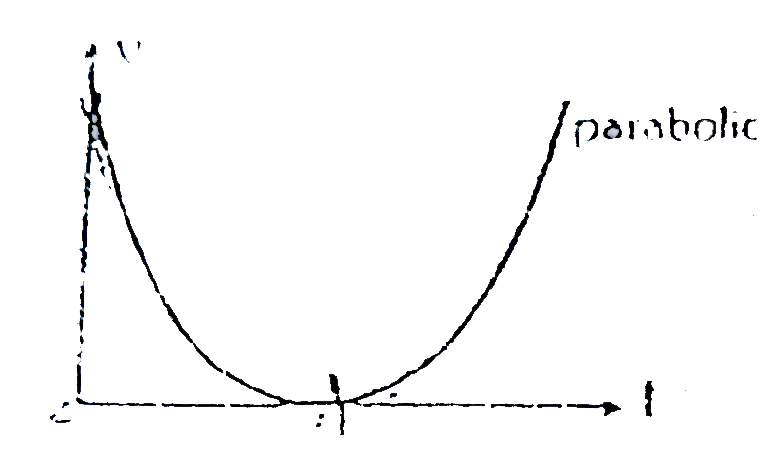 A
A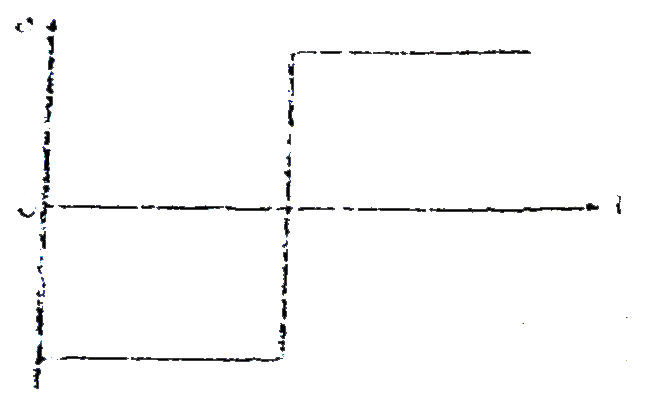 B
B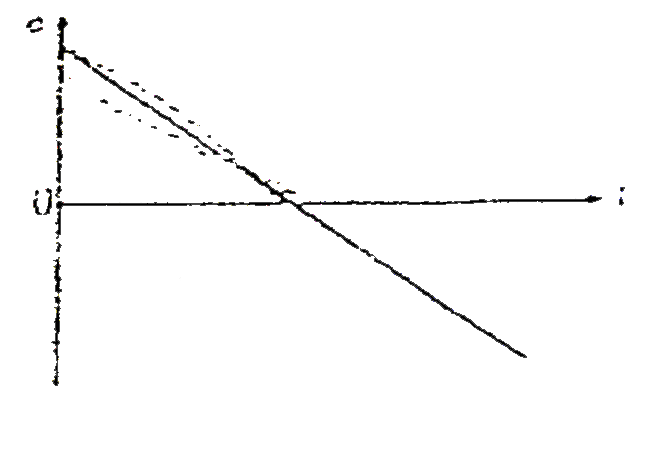 C
C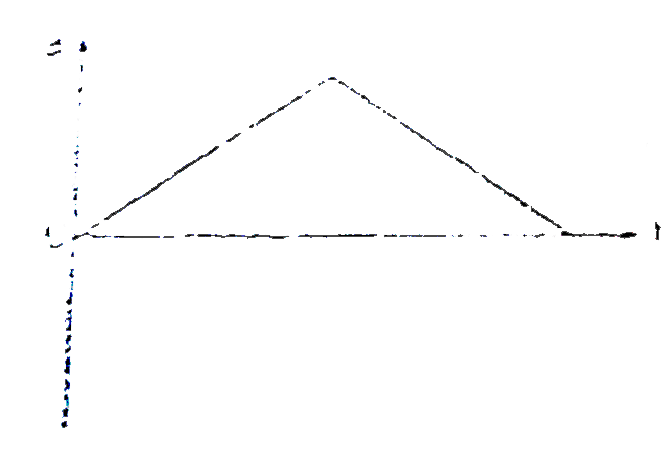 D
D
Velocity is given by v=4t(1−2t), then find time at which velocity is maximum
A0.25 sB1 sC0.45 sD4sA particle move with velocity v1 for time t1andv2 for time t2 along a straight line. The magntidue of its average acceleration is
Av2−v1t1−t2Bv2−v1t1+t2Cv2−t1t2−t1Dv1+v2t1−t2
A particle move with velocity v1 for time t1andv2 for time t2 along a straight line. The magntidue of its average acceleration is
View SolutionIf velocity v varies with time t as v=2t2, then the plot between v and t2 will be given as :
View SolutionIf velocity v varies with time t as v=2t2, then the plot between v and t2 will be given as :
View SolutionThe velocity of an object is changing with time and relation is given by the following equation.
v=2t+3t2
Calculate the position of the object from the origin at t=2s.
View SolutionIf velocity v varies with time t as v=2t2, then the plot between v and t2 will be given as :
View Solution
