A particle move with velocity v1 for time t1andv2 for time t2 along a straight line. The magntidue of its average acceleration is
v2−v1t1−t2
v2−v1t1+t2
v2−t1t2−t1
v1+v2t1−t2
The correct Answer is:B
To find the magnitude of the average acceleration of a particle moving with different velocities over specified time intervals, we can follow these steps:
1. Understand the Concept of Average Acceleration:
Average acceleration is defined as the change in velocity divided by the total time taken. Mathematically, it is given by:
aavg=ΔvΔt
where Δv is the change in velocity and Δt is the total time.
2. Identify the Given Variables:
- Initial velocity v1 for time t1
- Final velocity v2 for time t2
3. Calculate the Change in Velocity:
The change in velocity (Δv) can be calculated as:
Δv=v2−v1
4. Calculate the Total Time:
The total time (Δt) for which the particle is in motion is the sum of the two time intervals:
Δt=t1+t2
5. Substitute into the Average Acceleration Formula:
Now, substituting Δv and Δt into the average acceleration formula, we get:
aavg=v2−v1t1+t2
6. Conclusion:
The magnitude of the average acceleration of the particle is:
|aavg|=v2−v1t1+t2
Final Answer:
The magnitude of the average acceleration is v2−v1t1+t2.
---
Average acceleration is defined as the change in velocity divided by the total time taken. Mathematically, it is given by:
aavg=ΔvΔt
where Δv is the change in velocity and Δt is the total time.
- Initial velocity v1 for time t1
- Final velocity v2 for time t2
The change in velocity (Δv) can be calculated as:
Δv=v2−v1
The total time (Δt) for which the particle is in motion is the sum of the two time intervals:
Δt=t1+t2
Now, substituting Δv and Δt into the average acceleration formula, we get:
aavg=v2−v1t1+t2
The magnitude of the average acceleration of the particle is:
|aavg|=v2−v1t1+t2
The magnitude of the average acceleration is v2−v1t1+t2.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - B)
33 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - C)
36 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISE
29 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
Similar Questions
Acceleration time graph of a particle moving along a straight line is given. Then average acceleration between t=0 & t=4 is :−

View SolutionA person travelling on a straight line moves with a uniform velocity v1 for some time and with uniform velocity v2 for the next equal time. The average velocity v is given by
View SolutionA particle retards from a velocity v0while moving in a straight line. If the magnitude of deceleration is directly proportional to the square loop of the speed of the particle, find its average velocity for the total time of its motion.
View SolutionA body is moving with variable acceleartion (a) along a straight line. The average acceleration of body in time interval t1 to t2 is :-
View SolutionFigure shows the velocity time graph of a particle moving along straight line (v is m/s and t is in second). It average velocity in 20 seconds will be:
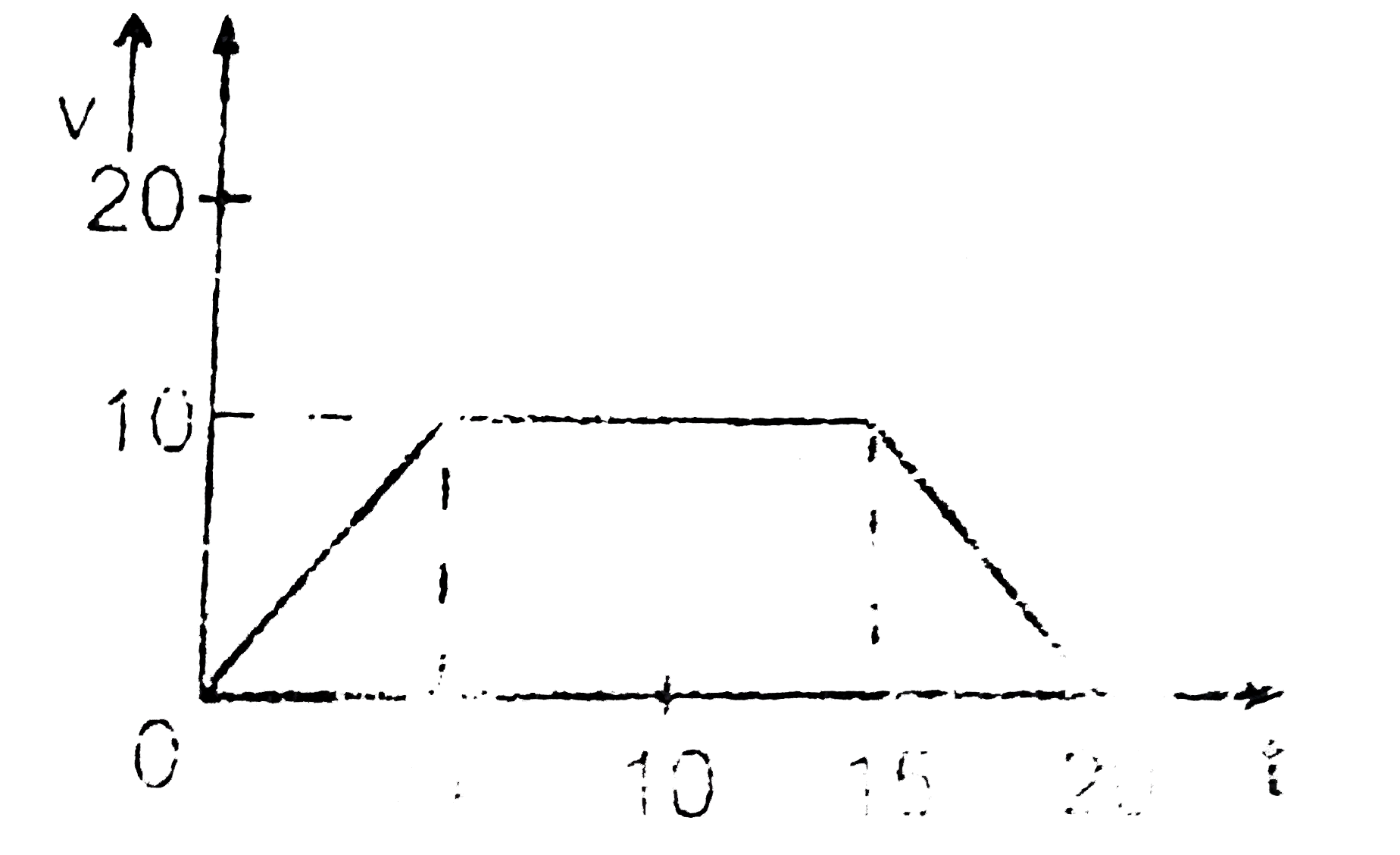 .
.
View SolutionThe velocity-time (v-t) graph for a particle in a straight line motion is given below The corresponding accelaration-time (a-t) graph will
View Solutionvelocity-time graph of a particle moving in a straight line is as shown in figure. At time t=0, velocity of the particle is zero. Find

(a) average acceleration in a time interval from t=6s to t=12s,
(b) velocity of the particle at t=14s.
View SolutionA block moves in a straight line with velocity v for time t0. Then, its velocity becomes 2v for next t0 time. Finally, its velocity becomes 3v for time T. If average velocity during the complete journey was 2. 5 v, then find T in terms of t0.
View SolutionA particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
View SolutionThe velocity (v)-time (t) graph of a partide moving along a straight line is as shown in the figure. The displacement of the particle from t = 0 to t = 4 is
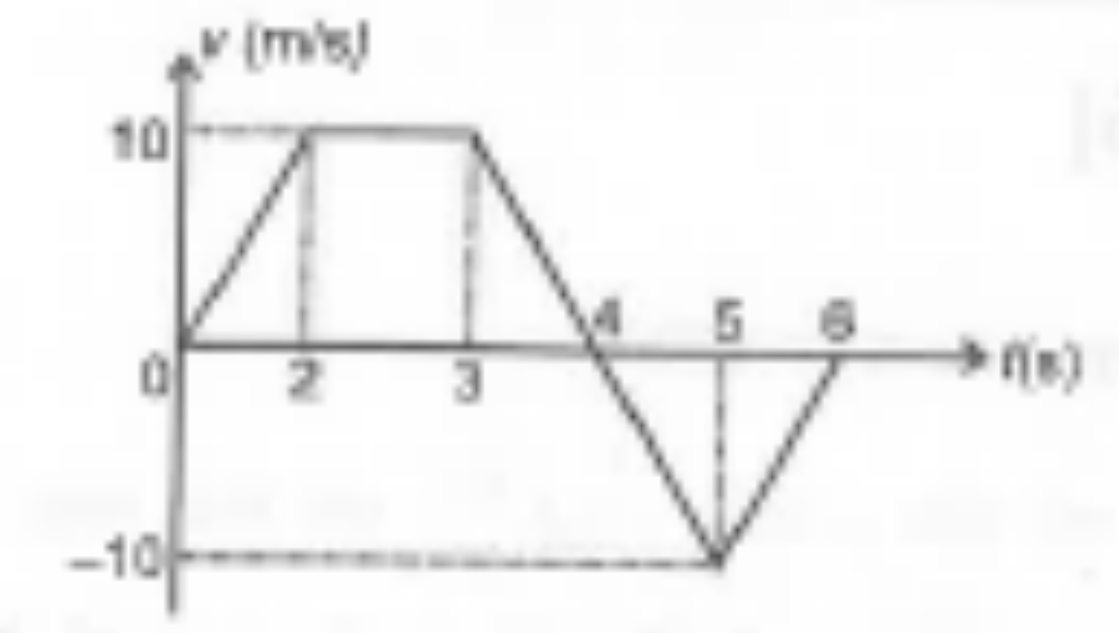
View Solution
