At what distance eye E will observe the fourth image (after four refractions from plane surfaces) of object O from itself.
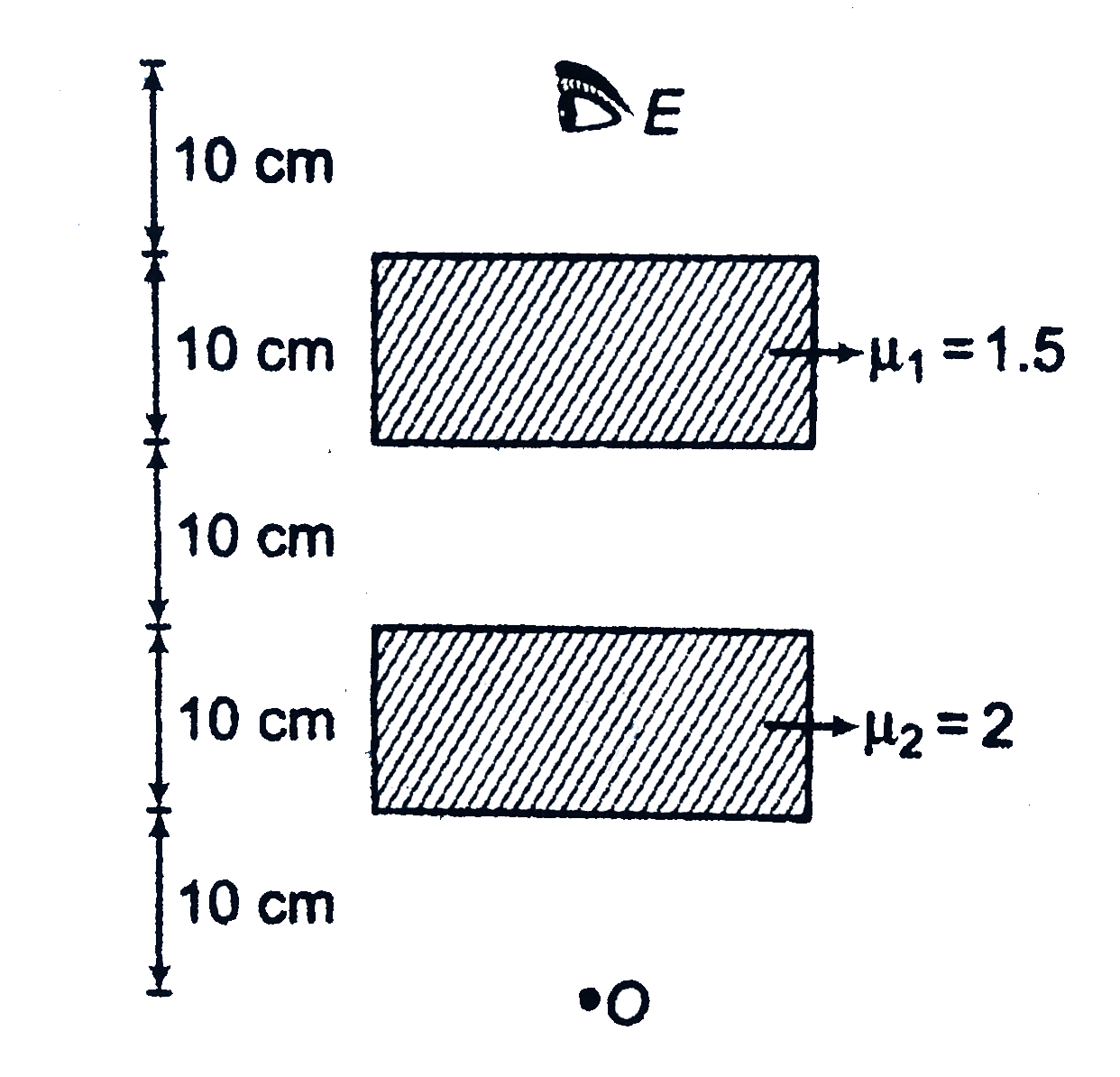
The correct Answer is:A, B, C
Total shift =(1−1μ1)t1+(1−1μ2)t2
=(1−23)10+(1−12)10
=253cm
∴ Image distance =50−253=1253cm
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.5
5 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.6
12 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Introductory exercise
4 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEYCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
Knowledge Check
An object is placed in front of a sphere of radius R at a distance x from the first surface. The value of x for which the light after refraction from the first surface becomes parallel to the axis is
ARμ−1BRμ+1C2R1+μDRμμ+1Figure shows a point object placed in front of a transparent sphere of radius 20 cm and refractive index 1.5. The sphere forms an image due to refraction at surface I followed by refraction at surface II. The sphere is kept in air and the object is located at distance x from P1. It is found that for x>x1, the image formed due to refraction at surface I is real, the final image formed by the sphere is also real and forms to the right of P2. For x2<x<x1, the image formed by surface I is virtual while the final image formed by the sphere is real and forms to the right of P2. However for x<x2, the image formed by surface I and also the final image formed by the sphere are virtual. It is also found that the final image is virtual if the distance of image formed by surface I from P2 is less than y. The object is now moved away from the sphere so that x becomes large and say, x→∞. In the given sphere is replaced by another one of the same radius but of refractive index 2.5, the final image is formed at distance y2 from P2.
For the object placed at x→∞, the given sphere of refractive index 1.5 forms an image at distance y1 from P2.
 Athis image is real and y1=12.5cm right of P2Bthis image is real and y1=10cm right of P2Cthis image is real and y1=20cm right of P2Dthis image is virtual and y1=12cm left of P2
Athis image is real and y1=12.5cm right of P2Bthis image is real and y1=10cm right of P2Cthis image is real and y1=20cm right of P2Dthis image is virtual and y1=12cm left of P2Figure shows a point object placed in front of a transparent sphere of radius 20 cm and refractive index 1.5. The sphere forms an image due to refraction at surface I followed by refraction at surface II. The sphere is kept in air and the object is located at distance x from P1. It is found that for x>x1, the image formed due to refraction at surface I is real, the final image formed by the sphere is also real and forms to the right of P2. For x2<x<x1, the image formed by surface I is virtual while the final image formed by the sphere is real and forms to the right of P2. However for x<x2, the image formed by surface I and also the final image formed by the sphere are virtual. It is also found that the final image is virtual if the distance of image formed by surface I from P2 is less than y. The object is now moved away from the sphere so that x becomes large and say, x→∞. In the given sphere is replaced by another one of the same radius but of refractive index 2.5, the final image is formed at distance y2 from P2.
As stated above, if the distance of image formed by Surface 1 from P2 is less than y, the final image is virtual. Then, y will be
 A40 cmB60 cmC80 cmD100 cm
A40 cmB60 cmC80 cmD100 cm
The image of an object placed in air formed by a convex refracting surface is at a distance of 10 m behind the surface. The image is real and is at 2rd3 of the distance of the object from the surface. The wavelength of light inside the surface is 23 times the wavelength in air. The radius of the curved surface is x13m. The value of 'x' is _________.
View SolutionObject O is placed in front of a plane mirror M. A glass slab S having thickness t = 3 cm and refractive index μ=1.8 is placed between the object and the mirror. The refracting faces of the slab are parallel to the mirror surface. The object is made to move with a velocity of u=2m/s perpendicular to the mirror surface. Find the speed of the image formed after
(a) refraction from the slab followed by reflection from the mirror.
(b) refraction from the slab followed by reflection from the mirror followed by the refraction from the slab.

View SolutionConsider the situation in Fig. The bottom of the pot is a reflecting plane mirror, S is a small fish, and T is a human eye. Refractive index of water is μ.
a. At what distance(s) from itself will the fish see the image(s) of the eye?
b. At what distance(s) from itself will the eye see the image(s) of the fish?

View Solution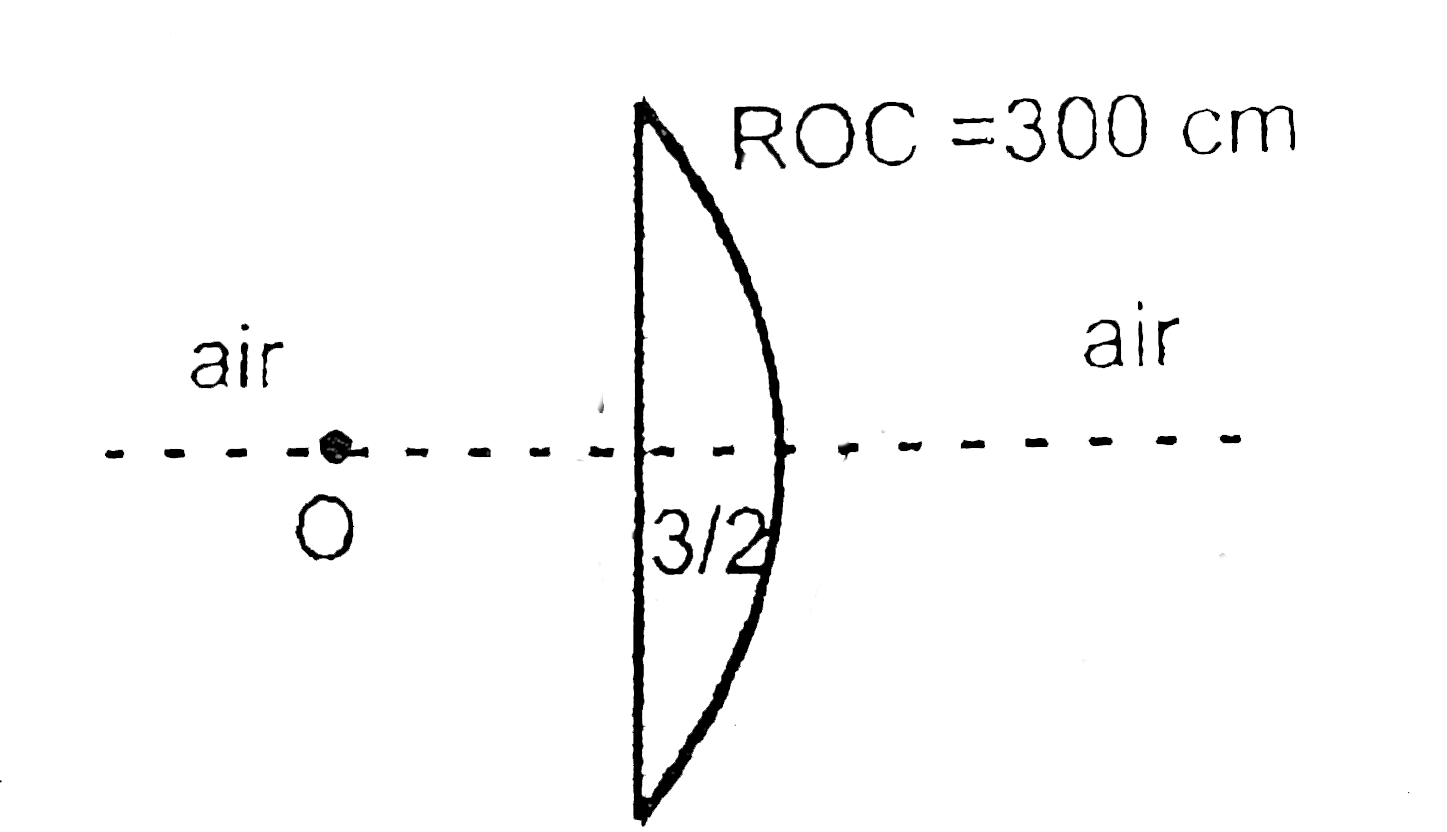
Plane surface of a thin planoconvex lens reflects 50% of light, while the curved surface is completely transparent, if final image of O after refraction through lens coinsides with the image formed due to partial reflection from plane surface. if distance (in m) between O and lens is x then find x/4
View SolutionFigure shows a point object placed in front of a transparent sphere of radius 20 cm and refractive index 1.5. The sphere forms an image due to refraction at surface I followed by refraction at surface II. The sphere is kept in air and the object is located at distance x from P1. It is found that for x>x1, the image formed due to refraction at surface I is real, the final image formed by the sphere is also real and forms to the right of P2. For x2<x<x1, the image formed by surface I is virtual while the final image formed by the sphere is real and forms to the right of P2. However for x<x2, the image formed by surface I and also the final image formed by the sphere are virtual. It is also found that the final image is virtual if the distance of image formed by surface I from P2 is less than y. The object is now moved away from the sphere so that x becomes large and say, x→∞. In the given sphere is replaced by another one of the same radius but of refractive index 2.5, the final image is formed at distance y2 from P2.
For the object placed at x→∞, a sphere of the same radius but of refractive index 2.5 forms an image at distance y2 from P2

View Solution
