At what maximum height with respect to the lowest point of a hollow sphere of radius r can a particle stay at rest inside it? Given the coefficient of friction between the sphere and the particle is μ.
Let m = mass of the particle, h =AC = maximum height of the point B where the particle can stay at rest Fig.
Normal force of the shpere on the particle, R = mg cos θ = component of the particle.s weight in the radial direction.

Topper's Solved these Questions
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - Section Related Questions
9 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - HIGHER ORDER THINKING SKILL ( HOTS ) QUESTIONS
14 Videos
- FIRST AND SECOND LAW OF THERMODYNAMICSBOOK - CHHAYA PUBLICATIONCHAPTER - FIRST AND SECOND LAW OF THERMODYNAMICSEXERCISE - CBSE SCANNER
18 Videos
- HYDROSTATICSBOOK - CHHAYA PUBLICATIONCHAPTER - HYDROSTATICSEXERCISE - CBSE SCANNER
1 Videos
Similar Questions
A hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
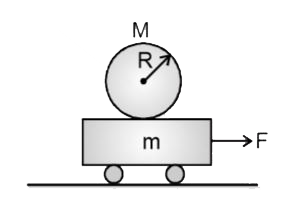
View SolutionDetermine the maximum horizontal force F that may be applied to the plank of mass m for which the solid sphere does not slip as it begins to roll on the plank. The sphere has a mass M and radius R. The coefficient of static and kinetic friction between the sphere and the plank are μsandμk respectively.
View Solution
Knowledge Check
A hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
AFriction opposes its translationBFriction supports rotation motionCOn decreasing θ, frictional force decreasesDAll of theseThe greatest height h of the sand pile that can be erected without spilling the sand onto the surrounding circular area of radius R (If μ is the coefficient of friction between sand particles) is
ARBRμCμRDμ2RA particle moving on the inside of a smooth sphere of radius r describing a horizontal circle at a distance r/2 below the centre of the sphere. What is its speed ?
A√5grB√4gr/3C√3gr/2D√√3gr

Determine the maximum horizontal force F that may be applied to the plank of mass m for which the solid sphere does not slip as it begins to roll on the plank. The sphere has a mass M and radius R. The coefficient of static and kinetic friction between the sphere and the plank are μS and μk respectively.
View SolutionA hollow sphere rolls down a rough inclined plane whose angle of inclination is θ, with horizontal. For the hollow sphere to undergo pure rolling, without slipping, the condition is [μ = coefficient of friction between the hollow sphere and inclined plane]
View SolutionA hollow sphere rolls down a rough inclined plane whose angle of inclination is θ, with horizontal. For the hollow sphere to undergo pure rolling, without slipping, the condition is [μ = coefficient of friction between the hollow sphere and inclined plane]
View SolutionA sphere of radius R is supported by a rope attached to the wall. The rope makes an angle θ=45∘ with respect to the wall. The point where the rope is attached to the wall is at a distance of 3R2 from the point where the sphere touches the wall. Find the minimum coefficient of friction (μ) between the wall and the sphere for this equilibrium to be possible.
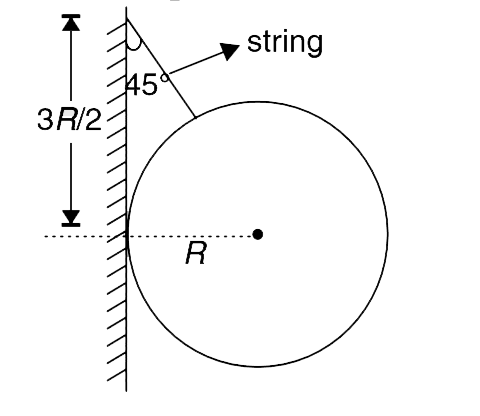
View SolutionA hollow sphere of radius r is rotating about a horizontal axis at some angular speed ω0. It is gently lowered to ground and the coefficient of friction between sphere and the ground is μ.How far does the sphere move before it starts pure rolling?
View Solution
