A sphere of radius R is supported by a rope attached to the wall. The rope makes an angle θ=45∘ with respect to the wall. The point where the rope is attached to the wall is at a distance of 3R2 from the point where the sphere touches the wall. Find the minimum coefficient of friction (μ) between the wall and the sphere for this equilibrium to be possible.
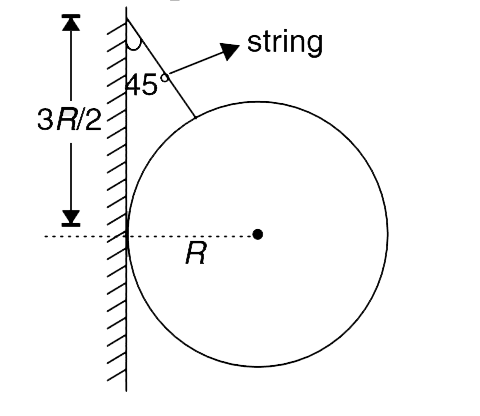
The correct Answer is:μmin=12
Topper's Solved these Questions
Similar Questions
A block weighing 4N is supported by two ropes Once rope is horizontal and the other makes an angle of 30∘ with the ceilling The tension (in newton) in the rope attached to the ceilling is .
View SolutionA ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View Solution
Knowledge Check
A 40 N block is supported by two ropes. One rope is horizontal and other makes an angle of 30∘ with the ceiling. The tension in the rope attached to the ceiling is approximately
A80 NB40 NC34.6 ND46.2 NA ladder 15m long makes an angle of 60∘ with the wall. Find the height of the point , where the ladder touches the wall.
A15√3B15√32mC152mD15mA 40 N block is supported by two ropes. One rope is horizontal and the other makes an angle of 30∘ with the ceiling. The tension in the rope attached to the ceiling is approximately :
A80 NB40 NC34.6 ND46.2 N
A ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View SolutionName the point of attachment of the cord to the wall of the uterus.
View SolutionIn the previous question instead of spherical wall there is a vertical wall at a perpendicular distance d from the point & where the light is incident.
View Solutiona uniform chain of lenght l has one of its end attached to a vertical wall at a point A whitle 3l\4 of the lenght of the chain is lying on A TABLE as shown in figure ,tangent to the chain at A makes an angle 37 with the wall find the minimumm coefficient of friction between table and chain so the chain remains at equilibrium
View SolutionA 22 m long ladder (whose foot is on the ground) leans against a wall making an angle of 60∘ with the wall. What is the height (in m) of the point where the ladder touches the wall from the ground?
View Solution
