Ball dropped from the top of a building. A the same instant ball is thrown vertically upwards from the ground. When the balls collide, they are moving in opposite directions and the speed of is twice the speed of . At what fraction of the height of the building did the collision occur?
The correct Answer is:
We are given the ratio of velocity of to the velocity of at the point of collision is same as the ration of height of this point form top of the building to the heitht height from the groun, let this ratio be .
form figure
Hence,
Hence,
2ghx=A) rArr z=(u^(2)-2A)/(u^(2))rArr x (1+(2gh)/(u^(2)))=1x=u^(2)/((u^(2)+2gh)xh =(u^(2)h)/(u^(2)+2gh)
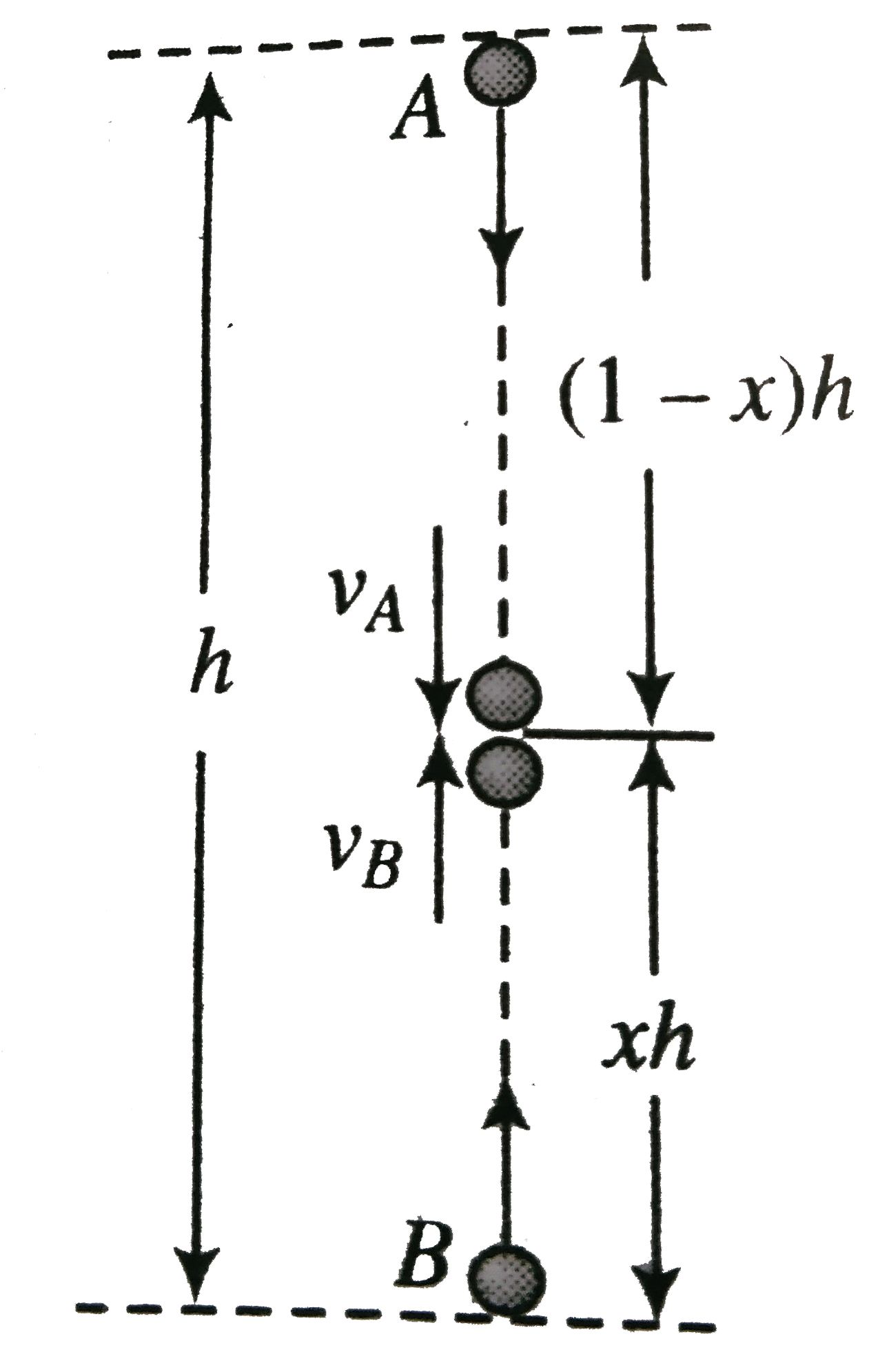 .
.
Topper's Solved these Questions
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Single Correct
Explore 52 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Graphical Concept
Explore 17 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Exercise 4.4
Explore 16 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Integer
Explore 9 Videos
Similar Questions
Ball A is dropped from the top of a building. At the same instant ball B is thrown vertically upwards from the ground. When the balls collide, they are moving in opposite direction and the speed of A is twice the speed of B. At what fraction of the height of the building did the collision occurs ?
View SolutionA ball is dropped from the top of a building 100 m high. At the same instant another ball is thrown upwards with a velocity of 40ms−1 from the bottom of the building. The two balls will meet after.
View Solution
Knowledge Check
A bal is thrown vertically upwards from the ground. It crosses a point at the height of 25 m twice at an interval of 4 secs. The ball was thrown with the velocity of
A20 m/sB25 m/sC30 m/sD35 m/s
A ball is dropped from the top of a building 100 m high. At the same instant another ball is thrown upwards with a velocity of 40ms−1 from the bottom of the building. The two balls will meet after.
View SolutionA ball is thrown vertically upwards from the top of tower of height h with velocity v . The ball strikes the ground after time.
View SolutionA ball is dropped from top of a tower 250 m high. At the same time, another ball is thrown upwards with a velocity of 50ms−1 from the ground. The time at which they cross each other is
View SolutionIf a ball is thrown upwards from the surface of earth :
View SolutionA ball is dropped from the top of a building of height 80 m. At same instant another ball is thrown upwards with speed 50 m/s from the bottom of the building. The time at which balls will meet is
View SolutionA ball of mass is thrown vertically upwards by applying a force by hand. If the hand moves while applying the force and the ball goes up to height further, find the magnitude of the force. (Take g=10ms−2)
View SolutionA ball dropped from the top of a building takes 0.5 sec to clear the window of 4.9 m height. What is the height of building above the window?
View Solution