Binary stars of comparable masses $m_{1}$ and $m_{2}$ rotate under the influence of each other's gravity with a time period $T$ . If they are stopped suddenly in their motions, find their relative velocity when they collide with each constant of gravitation.

Video Solution

Text Solution

Verified by Experts

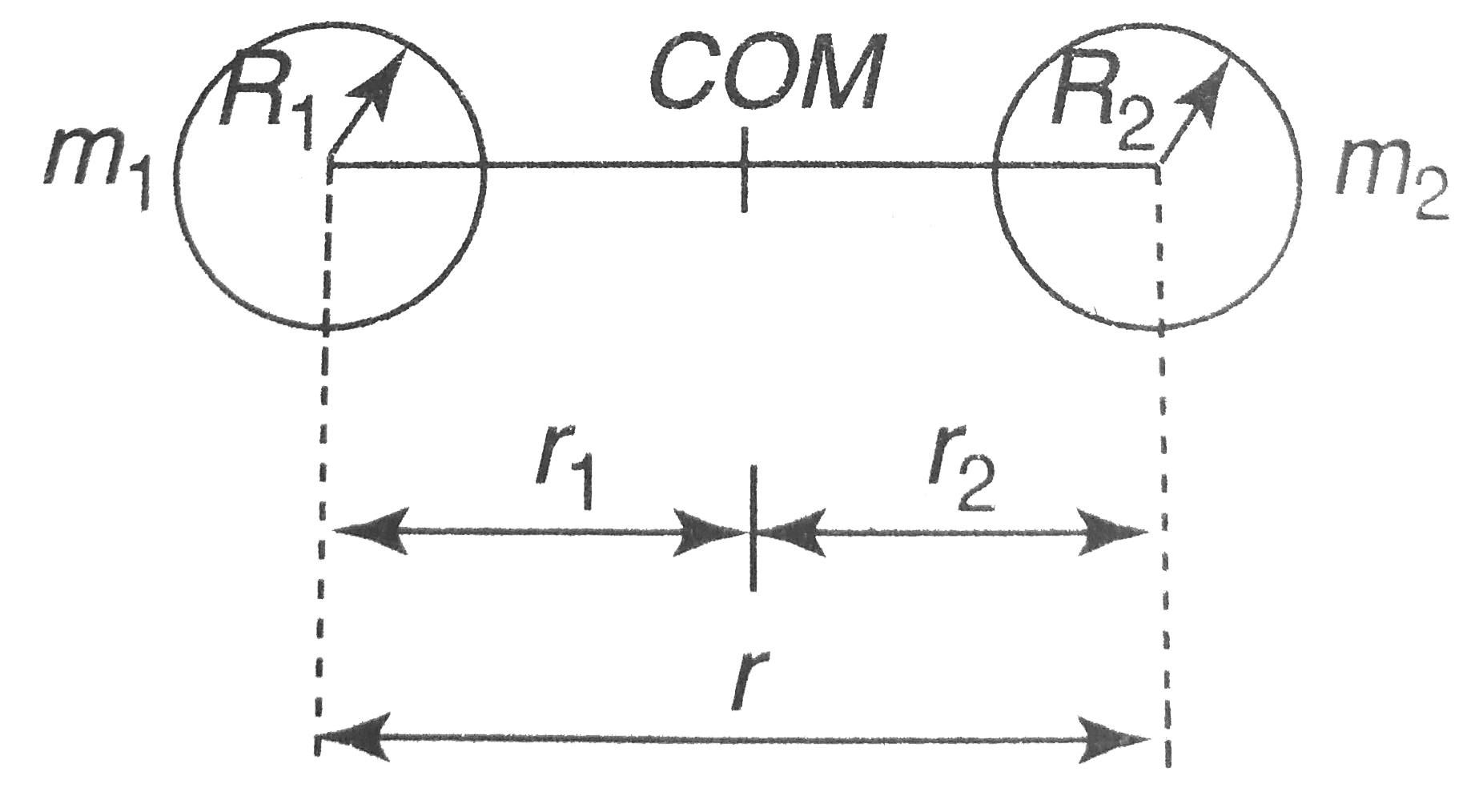
Both the stars rotate about their center of mass (COM).

For the position of $C O M$ , $\frac{r_{1}}{m_{2}} = \frac{r_{2}}{m_{1}} = \frac{r_{1} + r_{2}}{m_{1} + m_{2}} = \frac{r}{m_{1} + m_{2}}$ $(r = r_{1} + r_{2})$
Also $m_{1} r_{1} ω^{2} = \frac{G m_{1} m_{2}}{r_{2}}$
or $ω^{2} = \frac{G m_{2}}{r_{1} r^{2}}$ $(ω = \frac{2 π}{T})$
But, $r_{1} = \frac{m_{2} r}{m_{1} + m_{2}}$
$∴ ω^{2} = \frac{G (m_{1} + m_{2})}{r^{3}}$
or $r = {\frac{G (m_{1} + m_{2})}{ω^{2}}}^{1 / 3}$ ..(i)
Applying conservation of mechanical energy, we have
$- \frac{G m_{1} m_{2}}{r} = - \frac{G m_{1} m_{2}}{(R_{1} + R_{2})} + \frac{1}{2} μ υ_{r}^{2}$ ..(ii)
Hence, $μ =$ reduced mass
$= \frac{m_{1} m_{2}}{m_{1} + m_{2}}$
and $υ_{r} =$ relative between the two stars.
From Eq. (ii), we find that
$υ_{r}^{2} = \frac{2 G m_{1} m_{2}}{μ} (\frac{1}{R_{1} + R_{2}} - \frac{1}{r})$
$= \frac{2 G m_{1} m_{2}}{\frac{m_{1} m_{2}}{m_{1} + m_{2}}} (\frac{1}{R_{1} + R_{2}} - \frac{1}{r})$
$= 2 G (m_{1} + m_{2}) (\frac{1}{R_{1} + R_{2}} - \frac{1}{r})$
Substituting the value of $r$ from Eq. (i), we get
$υ_{r} = \sqrt{2 G (m_{1} + m_{2}) [\frac{1}{R_{1} + R_{2}} - {\frac{4 π^{2}}{G (m_{1} + m_{2}) T^{2}}}^{1 / 3}]}$

Updated on:21/07/2023