Blocks of masses 0.5 kg each, resting on a horizontal frictionless tabletop, are connected with an unstrethched speing of length L = 20 cm, and of spring constant 16 N/m. The mass of the spring is negligible art a certain moment the blocks are given an initial speed of v0=0.36m/s towards the wall. The block at the right collides with the wall elastically :
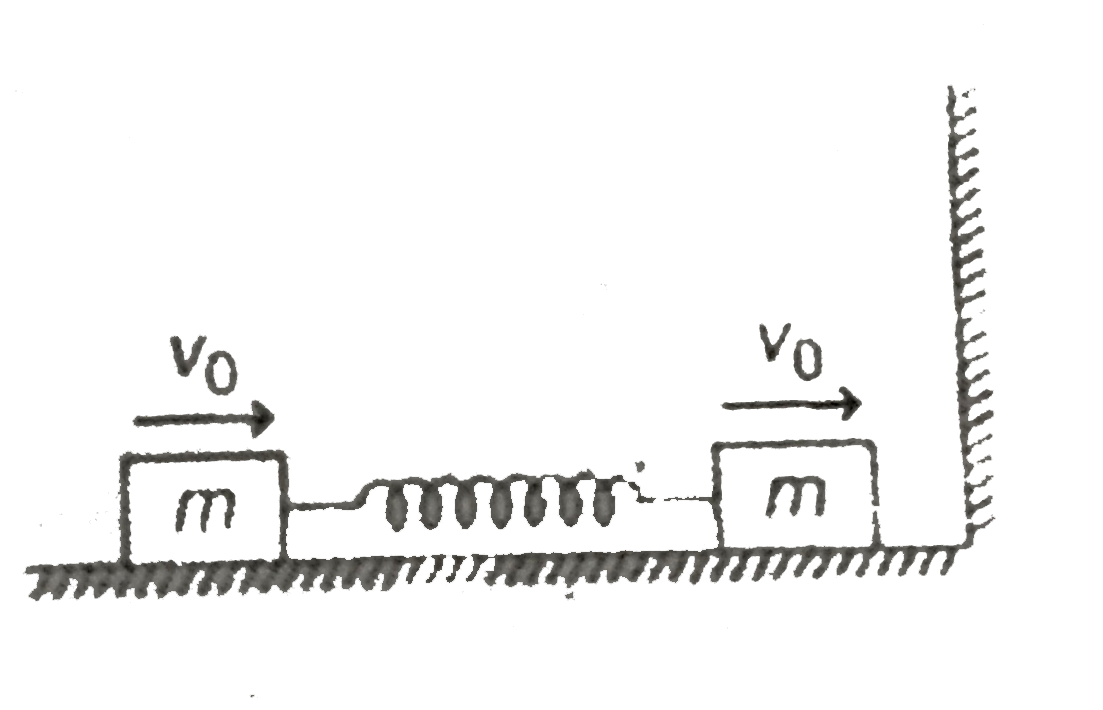
There will be 2 colllisions whith the wall
After 1st collision centre of mass comes to rest
After 2nd collision centre of mass moves to left with speed v0
After all collisions are over the system oscillates avout the centre of mass
Step by step video & image solution for Blocks of masses 0.5 kg each, resting on a horizontal frictionless tabletop, are connected with an unstrethched speing of length L = 20 cm, and of spring constant 16 N/m. The mass of the spring is negligible art a certain moment the blocks are given an initial speed of v_(0)=0.36m//s towards the wall. The block at the right collides with the wall elastically : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A mass of 0.5kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m The maximum compression of the spring would be.
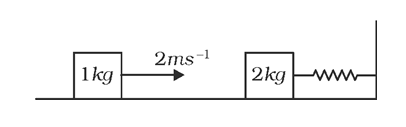
View SolutionA spring-block system is resting on a frictionless floor as shown in the figure. The spring constant is 2.0Nm−1 and the mass of the block is 2.0 kg. Ignore the mass of the spring. Initially the spring is in an unstretched condition. Another block of mass 1.0 kg moving with a speed of 2.0ms−1 collides elastically with the first block. The collision is such that the 2.0 kg block does not hit the wall. The distance, in metres, between the two blocks when the spring returns to its unstretched position for the first time after the collision is
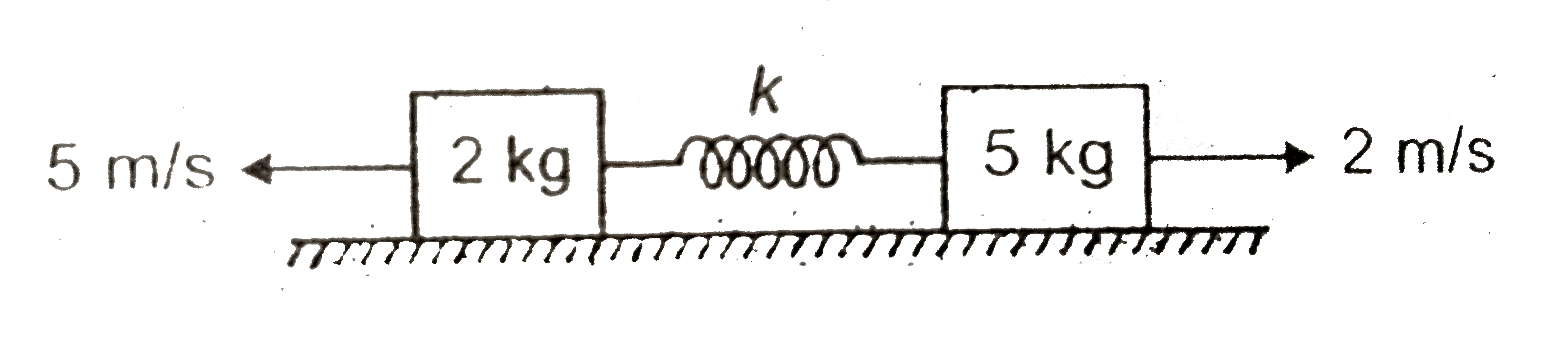
View SolutionTwo blocks of mass 2kg and 5kg are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant 35Nm. Find the maximum compression in the spring.
View SolutionTwo blocks A and B. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then

View SolutionTwo blocks A and B of mass 16kg and 64kg are placed on a smooth horizontal surface. Blocks are connected by a spring of spring constant 100N/m. Find the ratio of maximum speed of block A to maximum speed of block B.

View SolutionThe block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is

View SolutionA block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
View SolutionA block of mass 2kg is connected with a spring of natural length 40cm of force constant K=200N/m. The cofficient of friction is μ=0.5. When released from the given position, acceleration of block will be

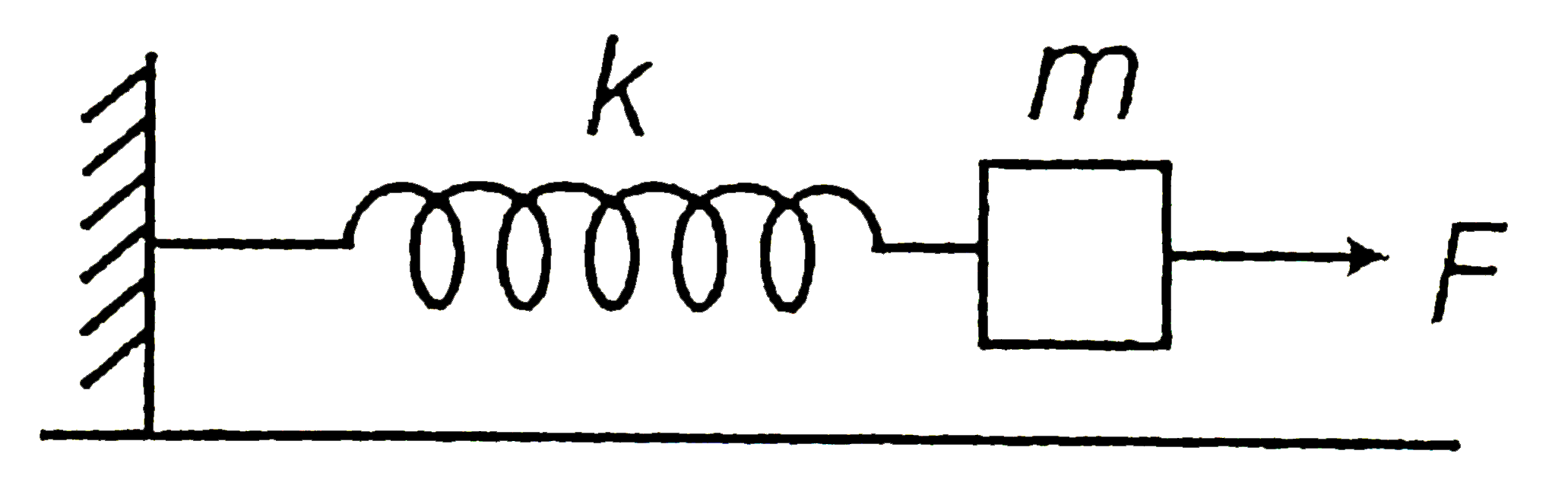
View SolutionThe figure showns a mass m on frictionless surface It is connected to righd wall by the mean of a massless spring of its constant K. Initially , The spring at its natural position.If a force of constant magnitude starts actiing on the block towareds right, then the speed of the block when the defromation in spring is x, will be
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View Solution