A block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
(a) MF(m+M)
(b) mFM
(c) (M+m)Fm
(d) mF(m+M)
The correct Answer is:D
Drawing free boy-diagrams for m & M,
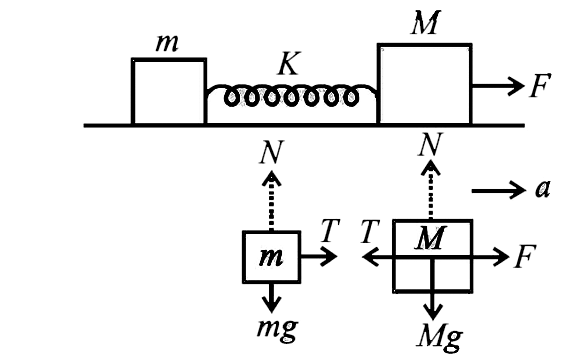
we get T=ma and F−T=Ma
where T is force due to spring
⇒F−ma=Ma or, F=Ma+ma
∴ a=FM+m
Now, force acting on the block of mass m is
ma=m(FM+m)=mFm+M
Topper's Solved these Questions
- HEAT AND THERMODYNAMICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - HEAT AND THERMODYNAMICSEXERCISE - JEE Main And Advanced
219 Videos
- MECHANICAL PROPERTIES OF MATTER AND FLUIDSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems
1 Video
Similar Questions
A block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant k. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M of pull it. Find the maximum extension of the spring
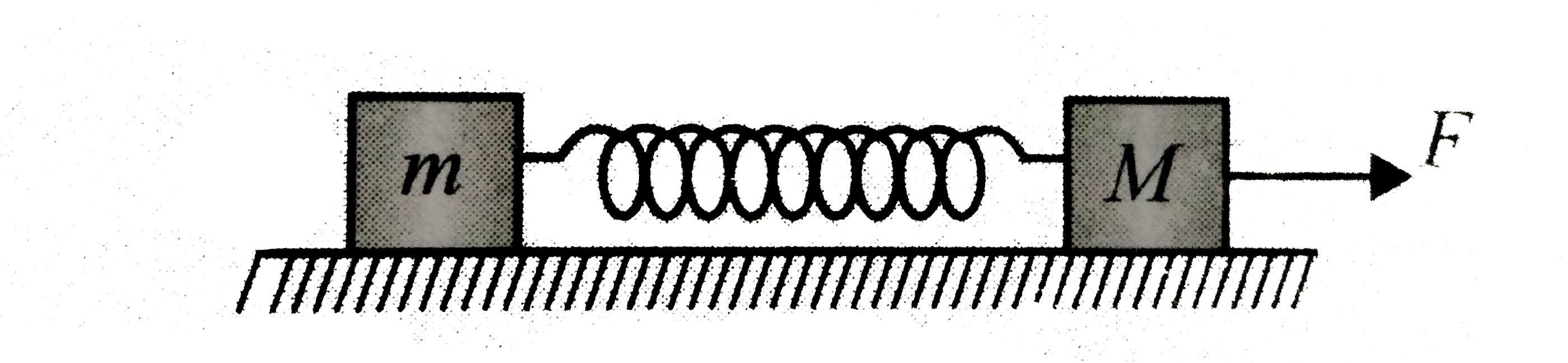
View Solution
Knowledge Check
A block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
AMF(m+M)BmFMC(M+m)FmDmF(m+M)In the figure shown, all surfaces are smooth and the pulley is massless. A constant force of magnitude F=mg2 is acting on the block of mass M. The acceleration of the block M is :
 Amg2(m+M) towards rightBmg2(m−M) towards rightsCmg2(m−M) towards leftDmg2(m+m) toward left
Amg2(m+M) towards rightBmg2(m−M) towards rightsCmg2(m−M) towards leftDmg2(m+m) toward leftFour blocks each of mass M connected by a massless strings are pulled by a force F on a smooth horizontal surface, as shown in figure.
 AT3=14FBT2=12FCT1=34FDT1=T2=T3=12F
AT3=14FBT2=12FCT1=34FDT1=T2=T3=12F
A block of mass m is connected to another block of mass M by a massless spring of spring constant K. Blocks are kept on a smooth horizontal plane. Initally both the blocks the at rest and spring is unstressed. Force F is applied on M to right as shownin the figure then which of the following is correct ?

View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA block of mass m=2kg is connected to a a spring of force constant k=50N/m. Initially the block is at rest and tlhe spring has natural length. A constant force F=60N is applied horizontally towards, the maximum speed of the block (in m/s) will be (negelect friction).

View SolutionTwo blocks connected by a spring rest on a smooth ITIM horizontal plane as shown in figure. A constant force F starts acting on block m2 as shown in the figure. Which of the following statements are not correct?

View Solution