Bob B of the pendulum AB is given an initial velocity √3Lg in horizontal direction. Final the maximum height of the bob from the starting point,
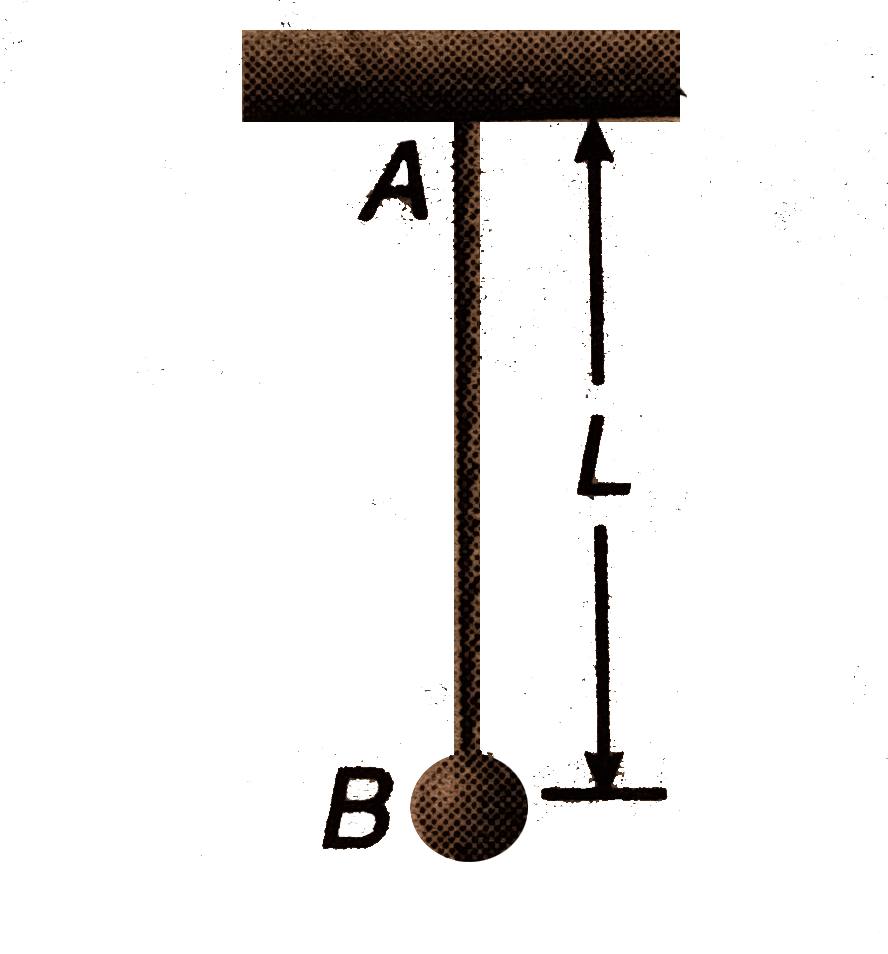
(a) if AB is a massless rod,
(b) if AB is a massless staring.
The correct Answer is:A, B, C, D
Applying conservation of energy
mgh=12m(√3Lg)2
oh=3L2
(b) Since, √3Lg lies between √2Lg and √5Lg , the stringt will slack in upper half of the circle. Assuming that string slack when it makes an angle θ with horizontal. We have
mgsinθ=mv2L ...(i)
v2=(√3gL2)−2gL(1+sinθ) ...(ii)
Solving Eq. (i) and Eq. (ii) , we get
sinθ=13
and v2=gL3
Maximum height of the bob from starting point,
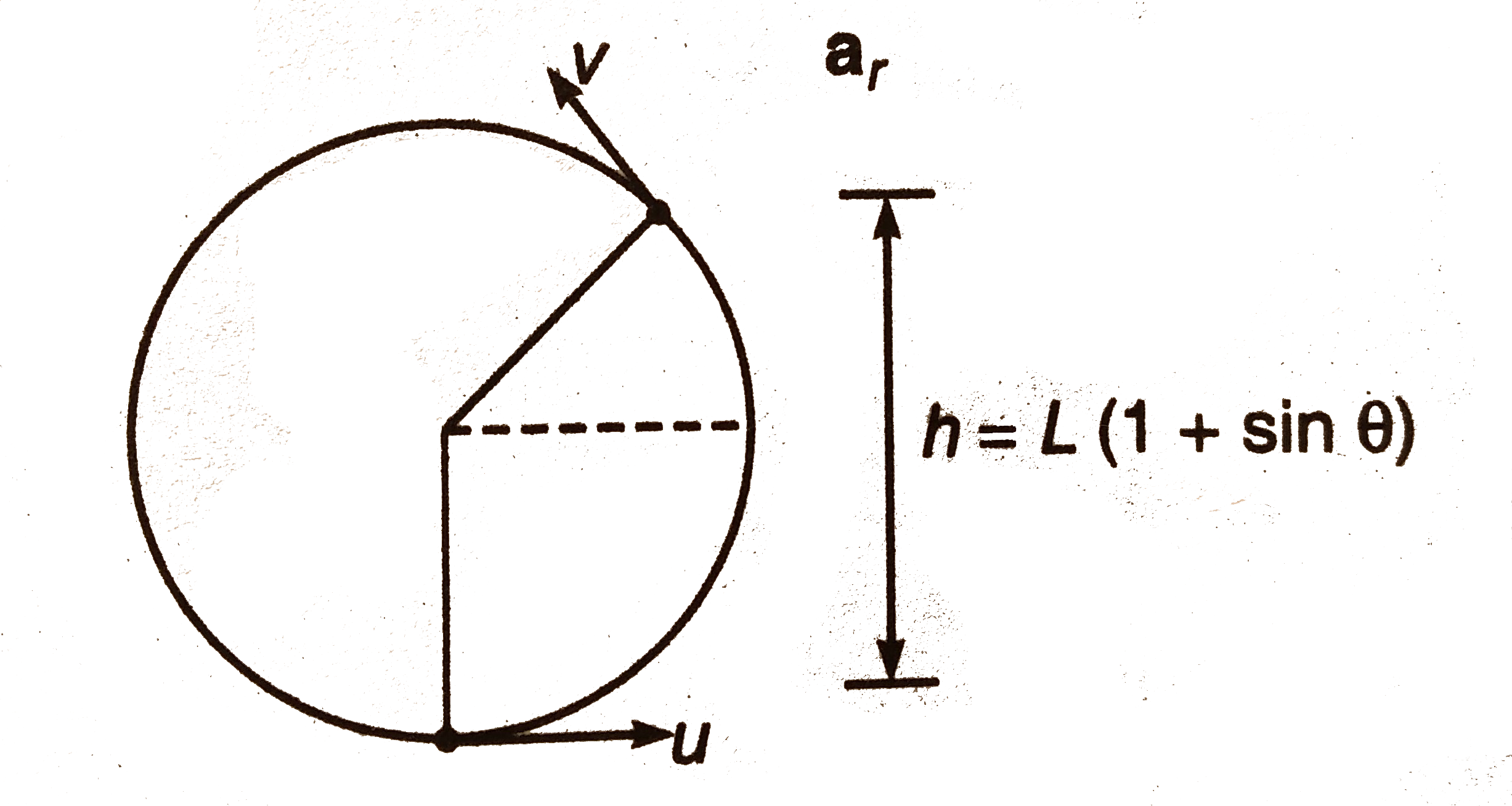
H=L(1+sinθ)+v2sin2(90∘−θ)2g
=4L3+(gL6g)cos2θ4L3+4L27
=4027L
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Subjective Questions
Explore 2 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:JEE Main
Explore 23 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Level 2 Comprehension Based
Explore 5 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
The bob of pendulum is project with horizontal velocity of √3gf I is the length of string. Find the angular displacement of string before it becomes slack.

View SolutionThe bob of a stationary pendulum is given a sharp hit to impart it a horizontal speed of √3gl. Find the angle rotated by the string before it becomes slack.
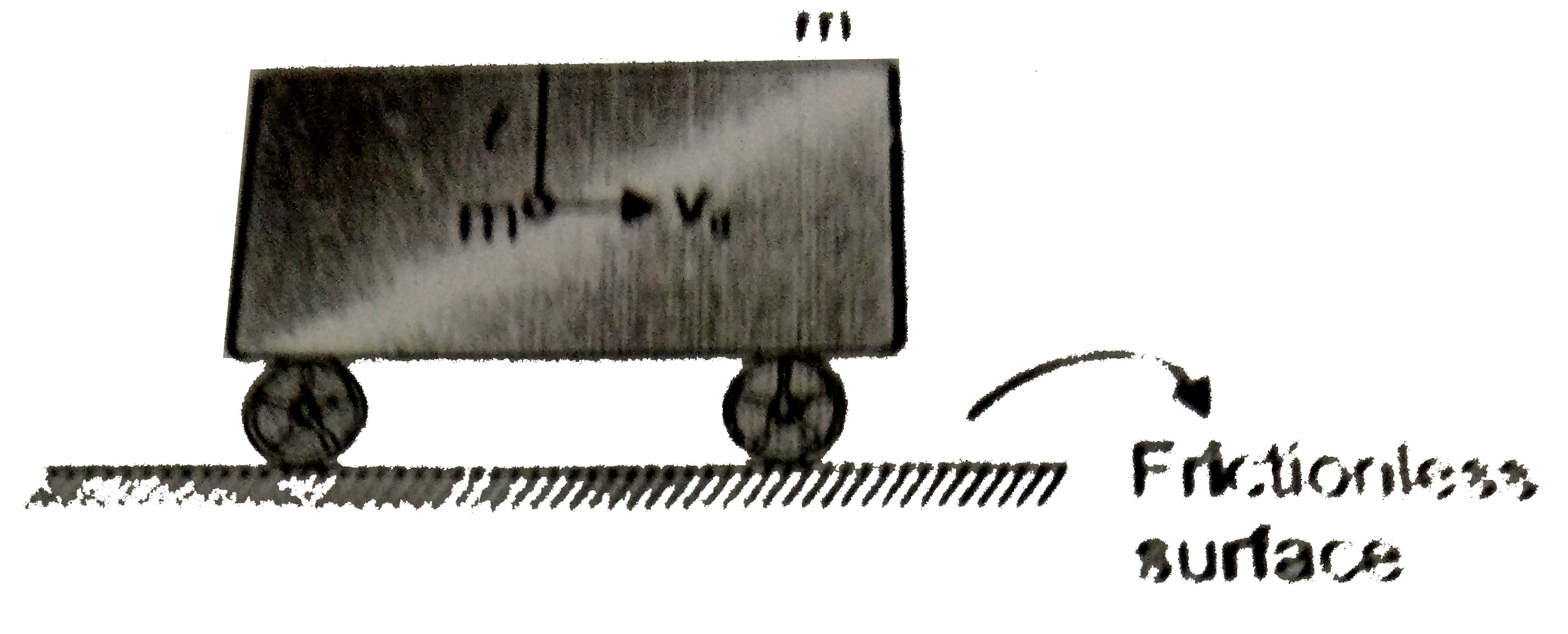
View SolutionA small bob mass 'm' is suspended by a massless string from a cart of the same mass 'm' as shown in the figure. The friction between the cart and horizontal ground is negligible. The bob is given a velocity V0 in horizontal direction as shown. The maximum height attained by the bob is , ( initially whole system ( bob + string + cart ) was at rest ).
View SolutionThe bob of a pendulum at rest is given a sharp hit to impart a horizontal velocity √10gl where l is the length of the pendulum. Find the tension in the string when a. the string is horizontal. B. The bob is at its highest point and c. the string makes an angle of 600 with the upward vertical.
View SolutionIn th efigure shown in fig. 10.33 , a bob attached with a light string of radius R is given as initial velocity u=√4gR at the bottommost point.
(a) At what height string will slack.
(b) What is velocity of the bob just befare slacking of string.
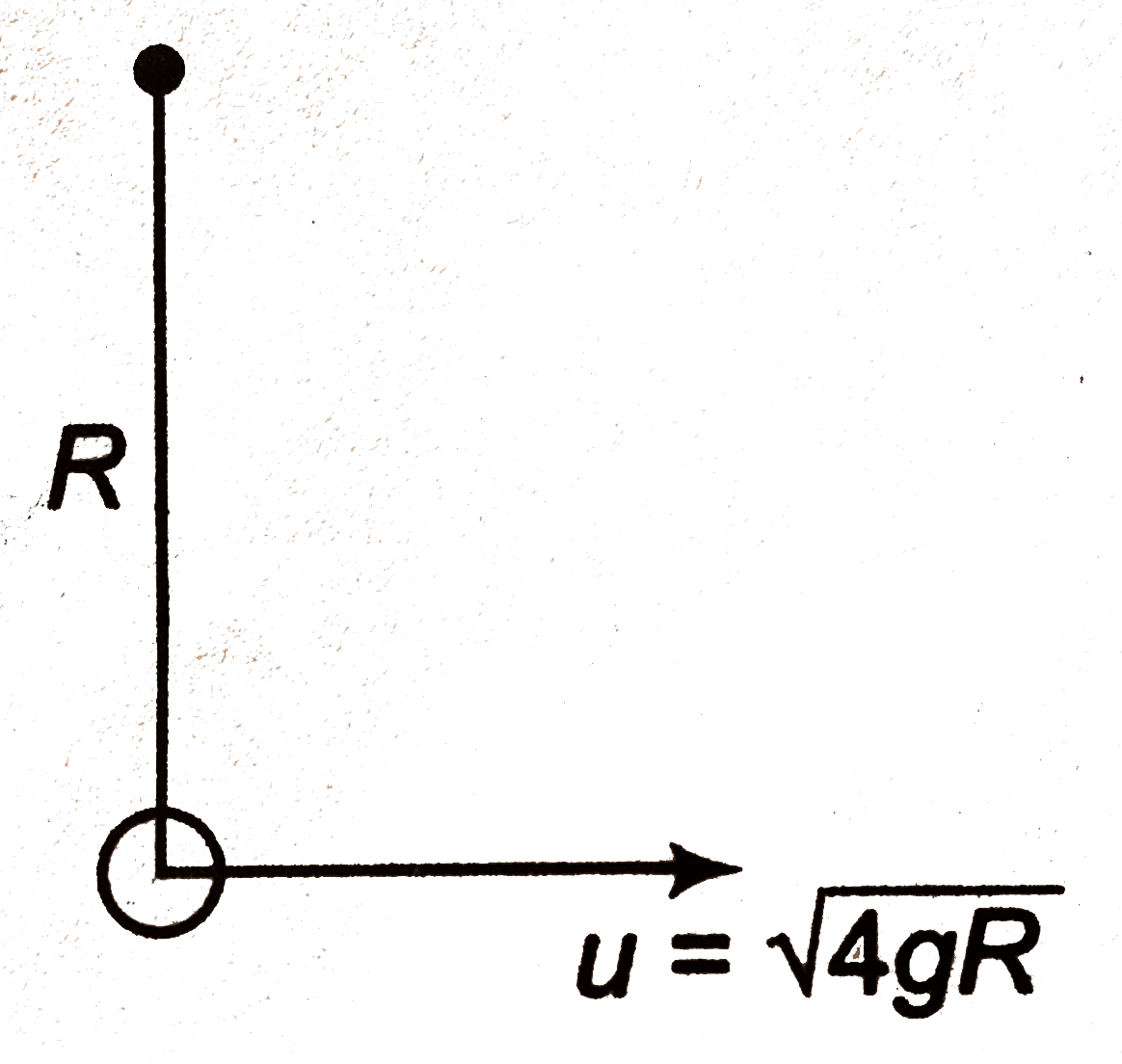
View Solution
Uniform rod AB is hinged at end A in horizontal position as shown in the figure. The other end is connected to a block through a massless string as shown. The pulley is smooth and massless. Mass of block and rod is same and is equal to m Then acceleration of block just after release from this position is
View SolutionA simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml23, the initial angular acceleration of the rod will be

View SolutionA rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio m/M
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Find the linear speed of the point P a time πL/3v0 after the collision.
View SolutionA rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio m/M
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Fid the linear speed of the point P a time πL/3v0 after the collision.
View Solution