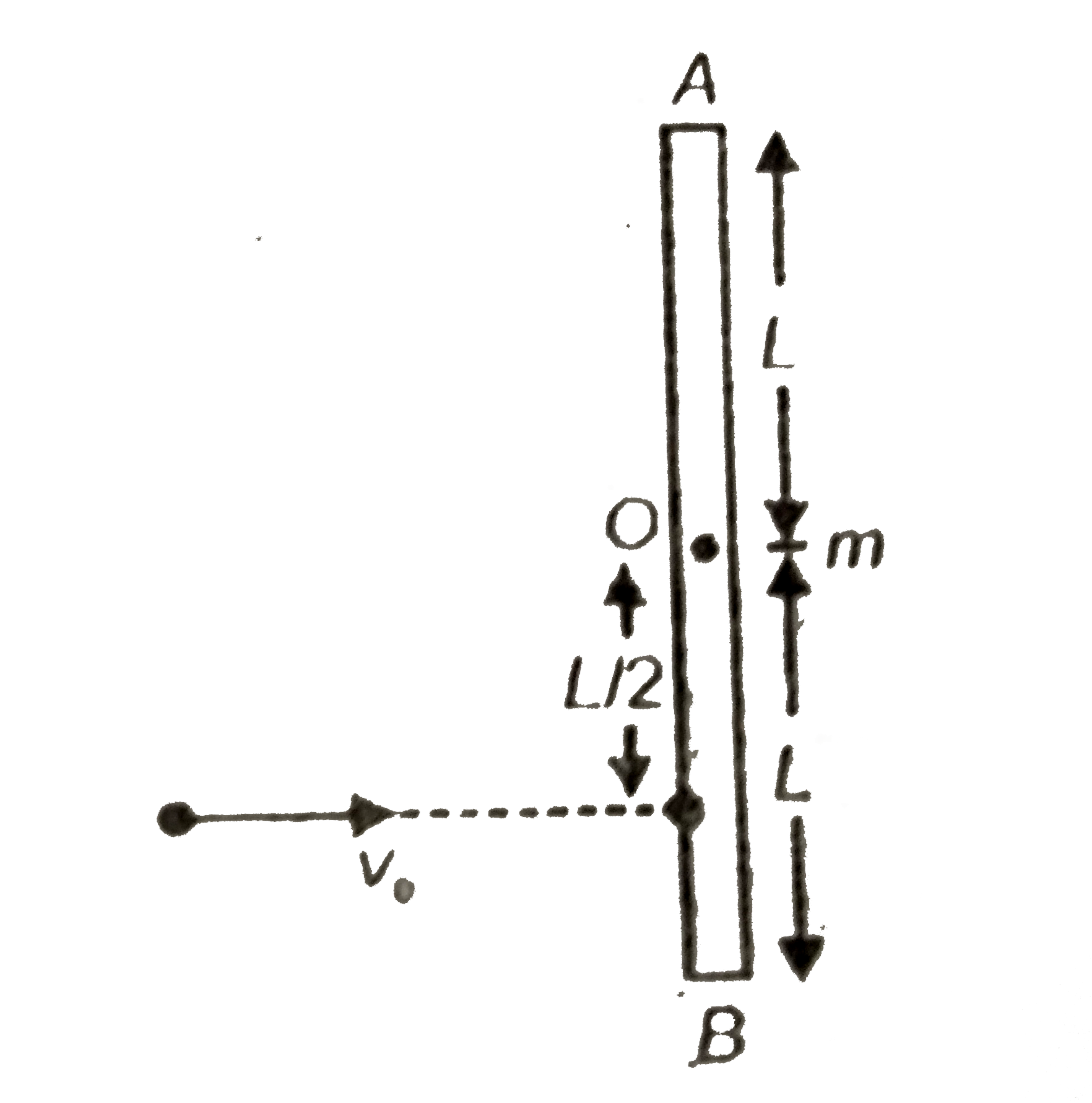
A rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio m/M
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Find the linear speed of the point P a time πL/3v0 after the collision.
Let us assume that speed of centre of mass of rod be v0 and angular speed about centre of mass be ω immediately after collision.
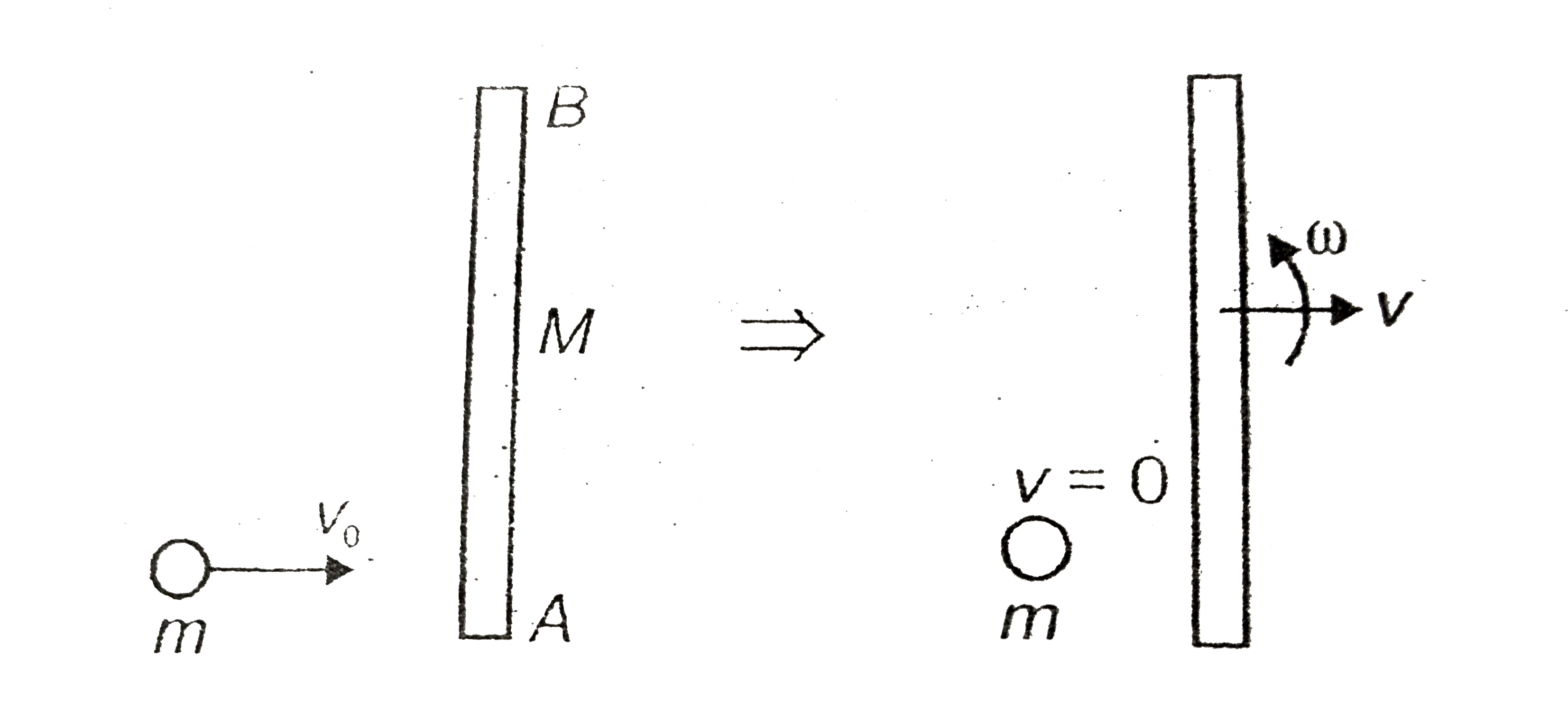
Taking the ball and rod to be part of a combined system, so for our system ∑Fext=0. So momentum can be conserved.
(a)∴mv0=MV⇒v=mMv0..........(1)
∑τ=0 about centre of rod. So conserving angular momentum
mv0⋅L2=ICM⋅ω⇒mv0L2=ML212ω
∴ω=6mMv0L..........(2)
Since the collision is perfectly elastic, K.E. of system will remain conserved.
12mv20=12MV2+12IC.M.⋅ω2 [Replacing the values of v and ω from equation (1) and (2) ]
⇒12mv20=12M(mMv0)2+12⋅ML212×36m2M2v20L2
or 1=mM+3mM=4mM
mM=14
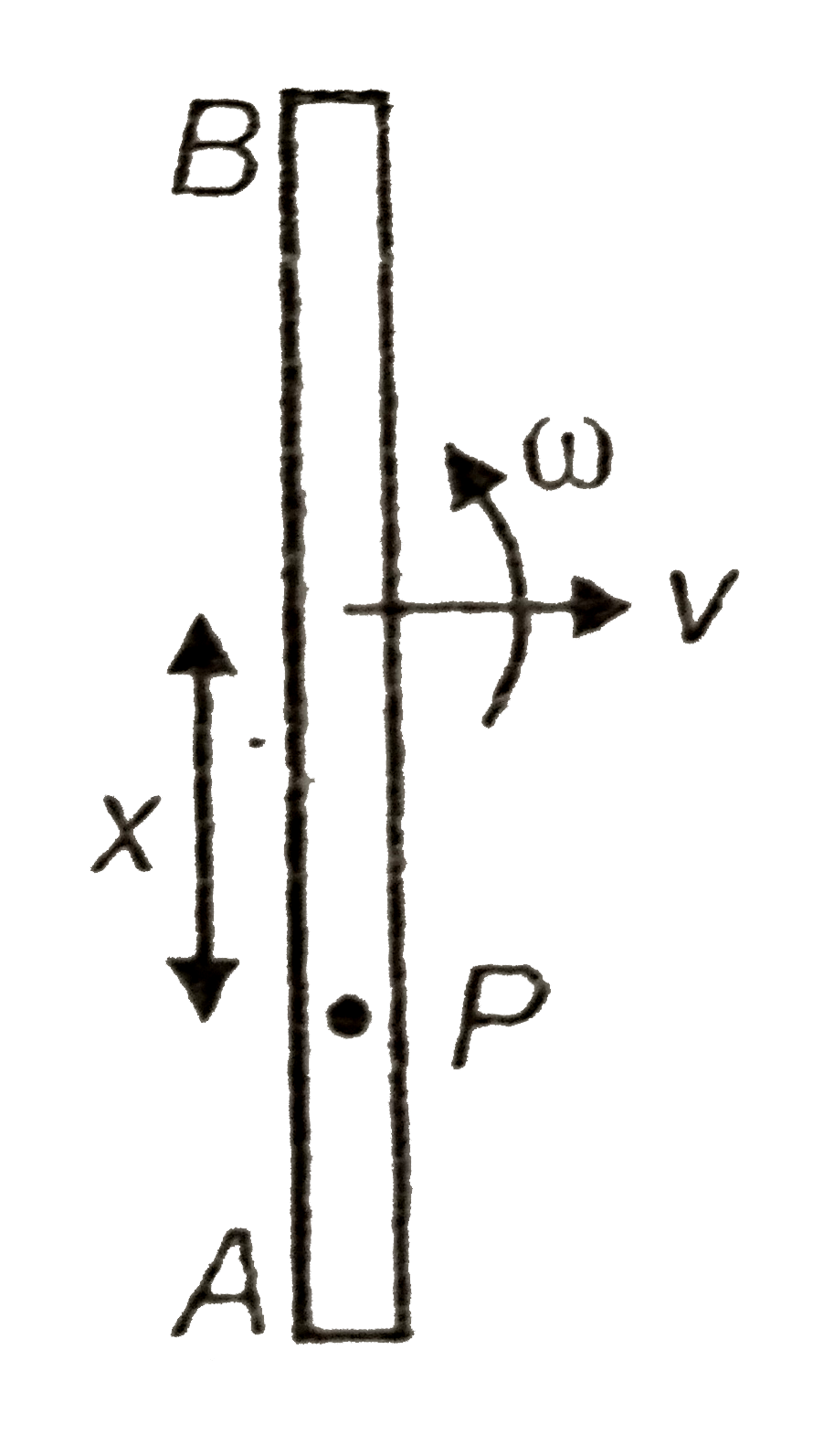
(b) For velocity of any point P to be zero immediately after the collision, the net velocity of point P is
v+ωx=0
∴x=−vω
=−mv0M⋅6mv0ML
∴=−L6
(-ve sign shows that the point will be on opposite side of what we have taken and is quite-logical too)
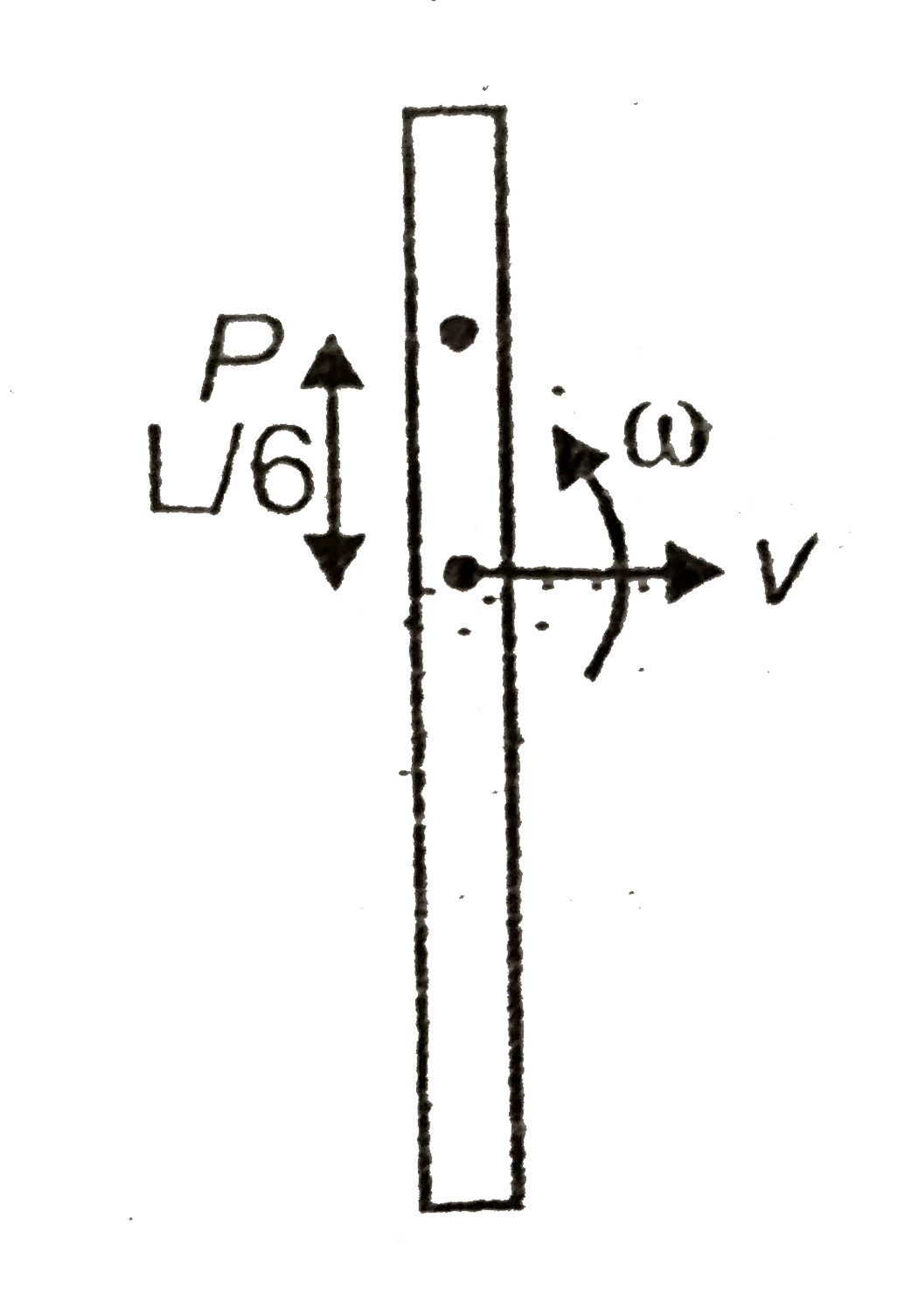
So, AP=L2+L6=4L6=2L3
(c) Just after collision,
v=mMv0=v04
ω=6mv0ML=3v02L
Since v=ωL6, both the translational speed as well as speed due to rotation will be equal to v=v04 at any time after collision.
After time t=πL3v0
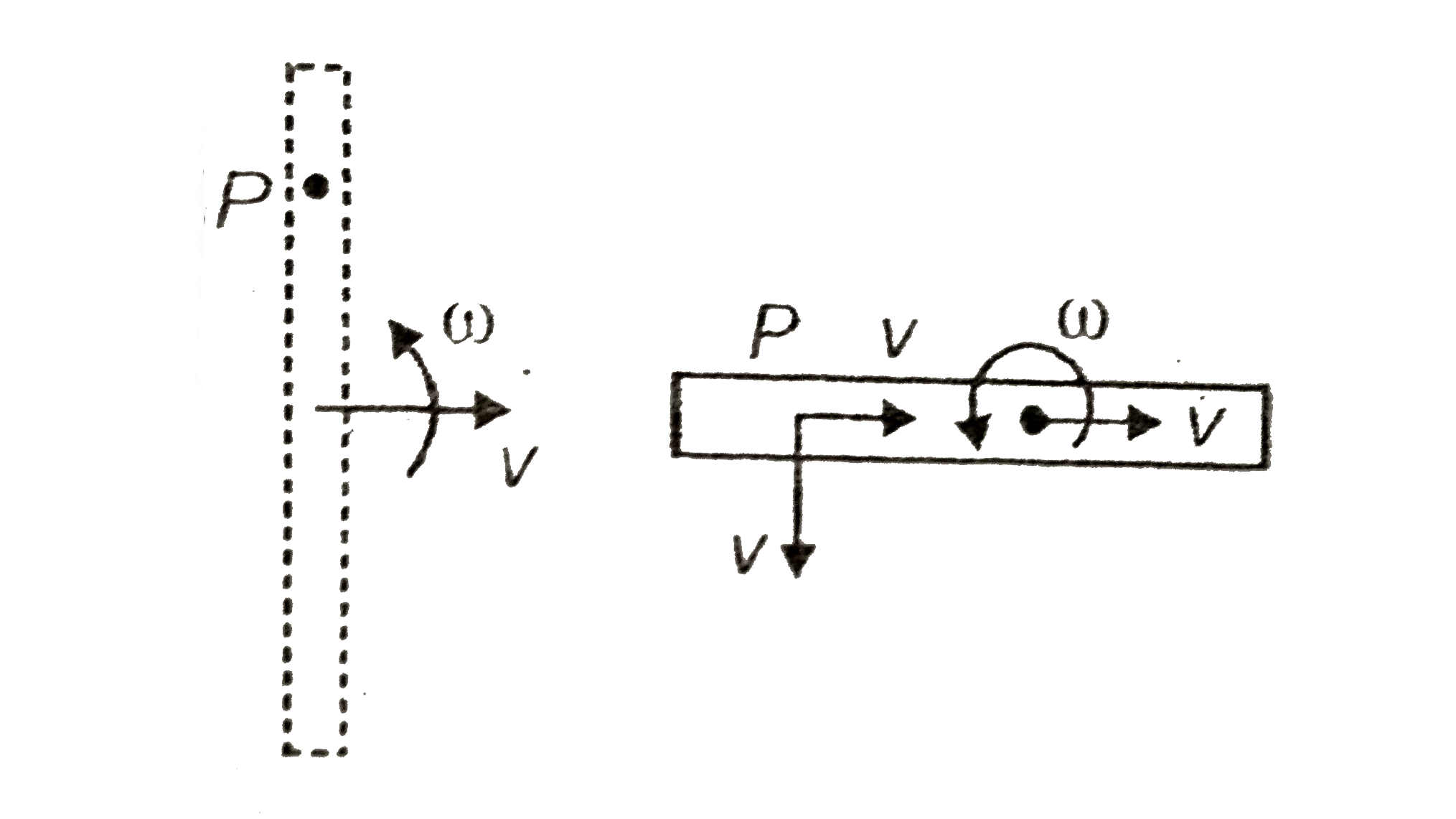
θ=ωt=3v02L×πL3v0=π2
So rad has turned by an angle π2, till that time after collision.
The point P has two velocities one in the direction of motion of cenre of rod and another perpendicular to the rod.
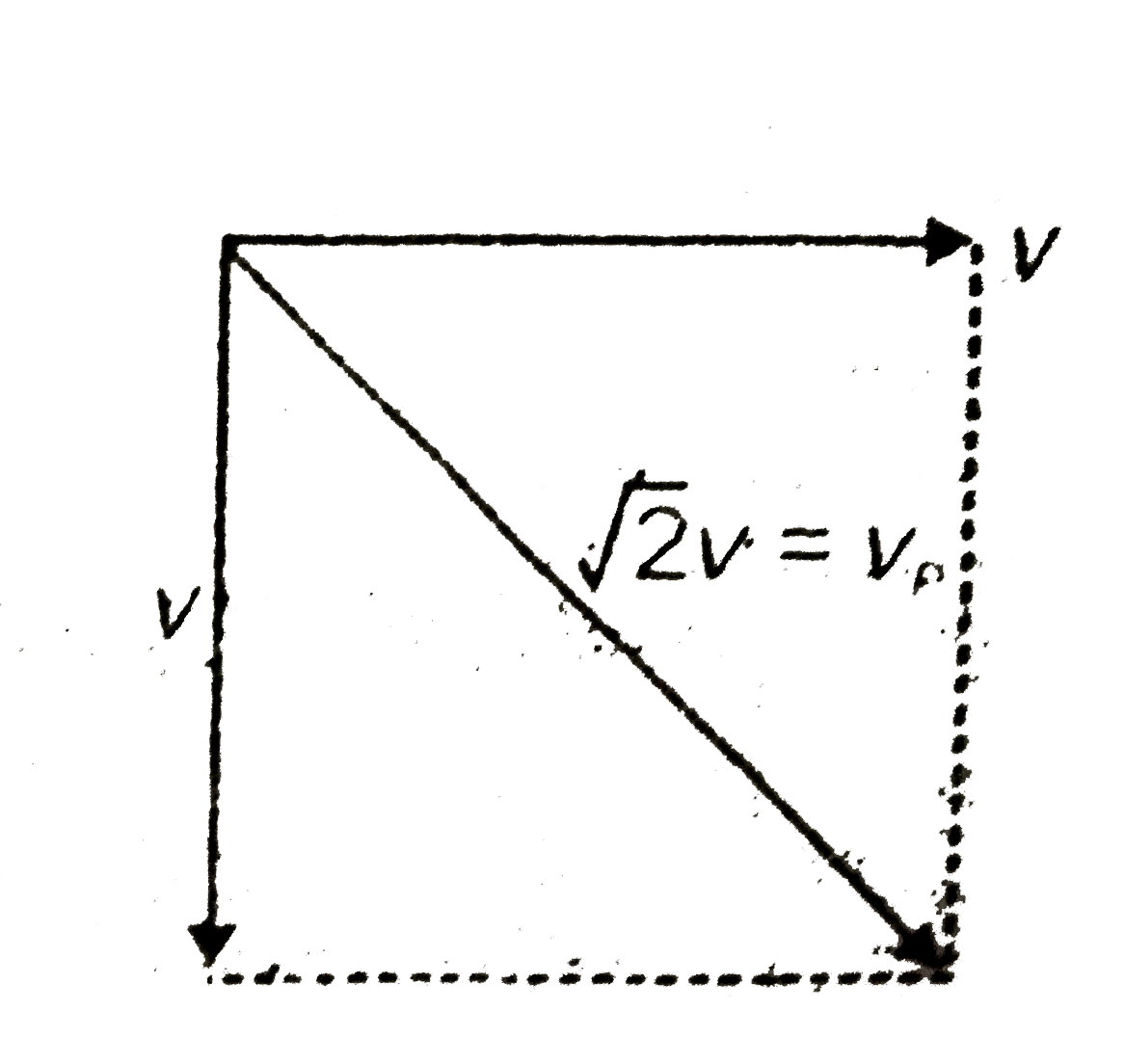
Resultant speed =√v2+v2=v√2=v04√2
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
A rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
Angular velocity of rod just after collision is
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.

Angular velocity of rod just after collision is
View SolutionA rod AC of length l and mass m is kept on a horizontal smooth plane. It is free to rotate and move. A particle of same mass m moving on the plane with velocity v strikes the rod at point B making angle 37∘ with the rod. The collision is elastic. After collision,

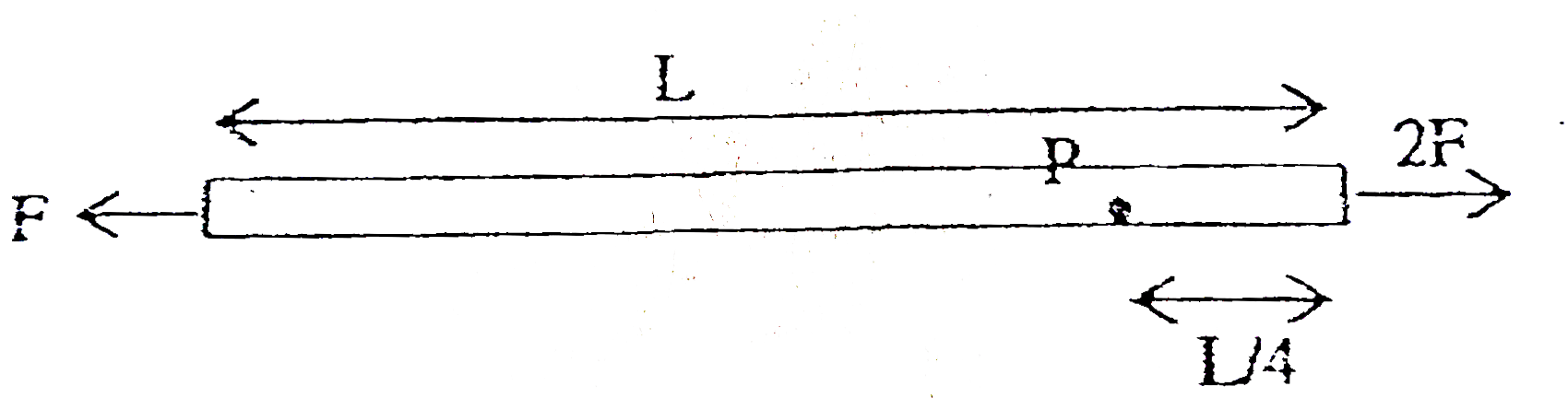
View SolutionA uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is
View SolutionA slender rod of mass M and length L rests on a horizontal frictionless surface. The rod is pivoted about one of ends. The impulse of the force exerted on the rod by the pivot when the rod is struck by a blow of impulse J perpendicular to the rod at other end is
View SolutionA straight rod AB of mass M and length L is placed on a frictionless horizontal surface. A force having constant magnitude F and a fixed direction start acting at the end A. The rod is initially perpendicular to the force. The initial acceleration of end B is
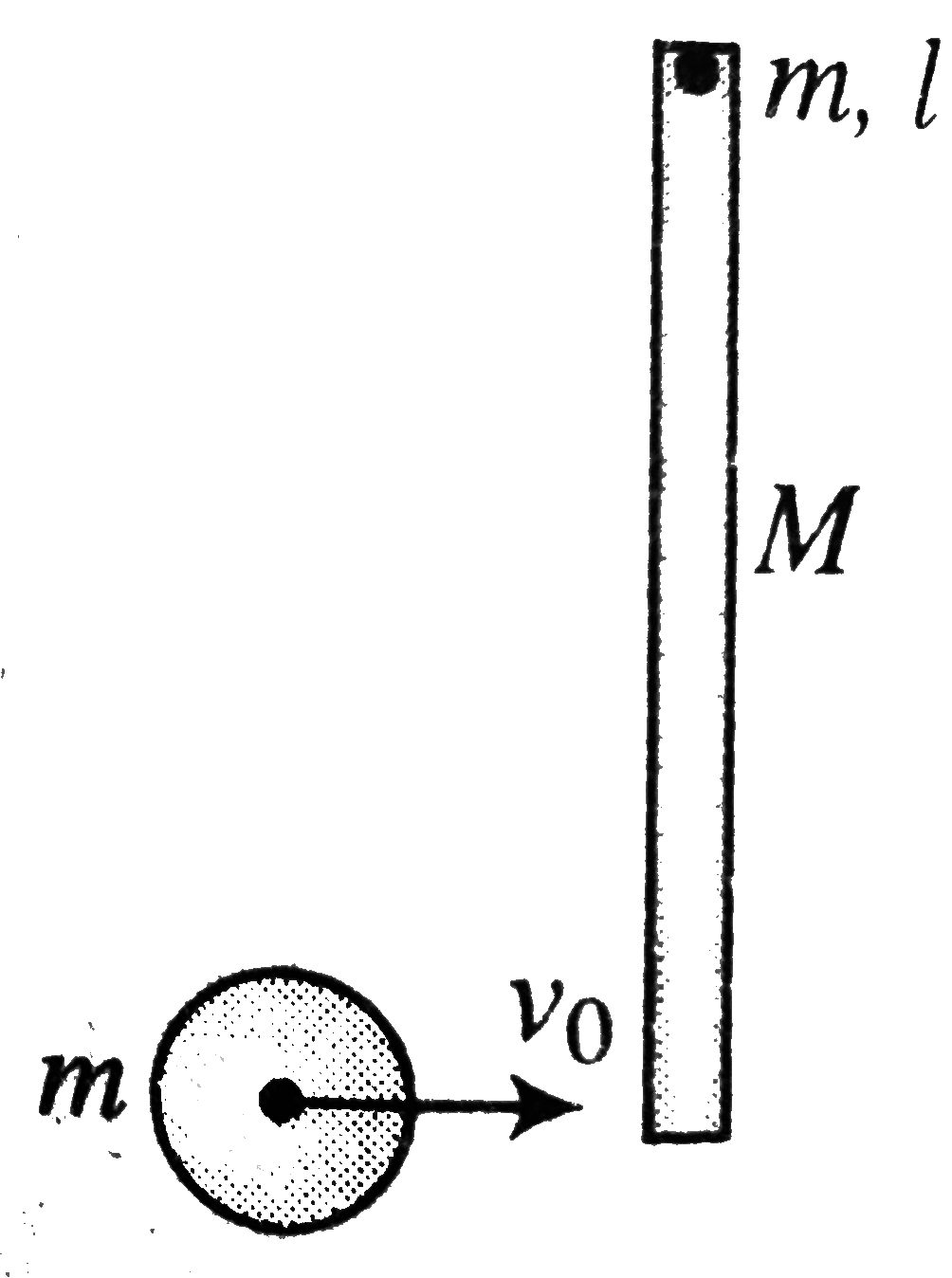
View SolutionA uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View SolutionA rod of mass m and length l in placed on a smooth table. An another particle of same mass m strikes the rod with velocity v0 in a direction perpendicular to the rod at distance x(<l/2) from its centre . Particle sticks to the end. Let ω be the angular speed of system after collision , then
As x is increased from 0 to l/2 , the angular speed ω.
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View Solution