By a cell a current of 0.9 A flows through 2 ohm resistor and 0.3A through 7 ohm resistor. The internal resistance of the cell is
0.5Ω
1.0Ω
1.2Ω
2.0Ω
The correct Answer is:A
To find the internal resistance of the cell, we can use the information provided about the current flowing through two different resistors connected to the same cell.
1. Identify the given values:
- Current through 2 ohm resistor, I1=0.9A
- Current through 7 ohm resistor, I2=0.3A
- Resistance of first resistor, R1=2Ω
- Resistance of second resistor, R2=7Ω
2. Use Ohm's Law and the concept of internal resistance:
The voltage across the cell can be expressed in terms of the current and resistance:
V=I1(R1+r)(for the first resistor)
V=I2(R2+r)(for the second resistor)
Here, r is the internal resistance of the cell.
3. Set up the equations:
From the first case:
V=0.9(2+r)(1)
From the second case:
V=0.3(7+r)(2)
4. Equate the two expressions for V:
Since both expressions equal V, we can set them equal to each other:
0.9(2+r)=0.3(7+r)
5. Expand both sides:
1.8+0.9r=2.1+0.3r
6. Rearrange the equation:
Move all terms involving r to one side and constant terms to the other:
0.9r−0.3r=2.1−1.8
0.6r=0.3
7. Solve for r:
r=0.30.6=0.5Ω
Final Answer:
The internal resistance of the cell is r=0.5Ω.
---
- Current through 2 ohm resistor, I1=0.9A
- Current through 7 ohm resistor, I2=0.3A
- Resistance of first resistor, R1=2Ω
- Resistance of second resistor, R2=7Ω
The voltage across the cell can be expressed in terms of the current and resistance:
V=I1(R1+r)(for the first resistor)
V=I2(R2+r)(for the second resistor)
Here, r is the internal resistance of the cell.
From the first case:
V=0.9(2+r)(1)
From the second case:
V=0.3(7+r)(2)
Since both expressions equal V, we can set them equal to each other:
0.9(2+r)=0.3(7+r)
1.8+0.9r=2.1+0.3r
Move all terms involving r to one side and constant terms to the other:
0.9r−0.3r=2.1−1.8
0.6r=0.3
r=0.30.6=0.5Ω
The internal resistance of the cell is r=0.5Ω.
Topper's Solved these Questions
- BOOK - ERRORLESS CHAPTER - CURRENT ELECTRICITYEXERCISE - Kirchhoff s Law, cells8videos
CURRENT ELECTRICITY
- BOOK - ERRORLESS CHAPTER - CURRENT ELECTRICITYEXERCISE - Different Measuring Instruments1videos
CURRENT ELECTRICITY
- BOOK - ERRORLESS CHAPTER - COMMUNICATION SYSTEMEXERCISE - S E T14videos
COMMUNICATION SYSTEM
- BOOK - ERRORLESS CHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - SET20videos
ELECTRO MAGNETIC INDUCTION
Similar Questions
Knowledge Check
- Question 1 - Select One
A current of 2 A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5 A when connected across a 9 Ω resistor. The internal resistance of the battery is
A1ΩB2ΩC13ΩD14Ω - Question 2 - Select One
A current of 2A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5A when connected across a 9Ω resistor. The internal resistance of the battery is
A1/3ΩB1/4ΩC1ΩD0.5Ω - Question 3 - Select One
When two identical cells are connected either in series or in parallel across a 4 ohm resistor, they send the same current through it. The internal resistance of the cell in ohm is
A4ΩB2ΩC1ΩD7Ω
A battery supplies a current of 0.9 A through a 2Ω resistor and a current of 0.3 A through a 7Ω resistor. Calculate the emf and internal resistance of the battery.
View SolutionA current of 2A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5A when connected across a 9Ω resistor The internal resistance of the battery is
View SolutionA current of 0.1 A flows through a 25 Ω resistor represented by the circuit diagram. The current in the 80 Ω resistor is
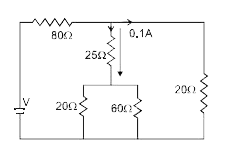 View Solution
View SolutionTwo identical cells connected in series send 1.0A current through a 5Ω resistor. When they are connected in parallel, they send 0.8 A current through the same resistor. What is the internal resistance of the cell?
View SolutionA cell of 2.1 V gives 0.2 A current through resistance 10Ω The internal resistance is:
View Solution


