By vector method, prove that if the diagonals of a parallelogram intersect perpendicularly,then the parallelogram is rombus.

Video Solution

Text Solution

Verified by Experts

Assuming the sides of a paralleogram as $- - \to O P = \to A$ , and $- - \to O R = \to B$ ,
its diagonals can be given as $- - \to O Q = \to A + \to B$ and $- - \to R P = \to A - \to B$ ,
respectively.

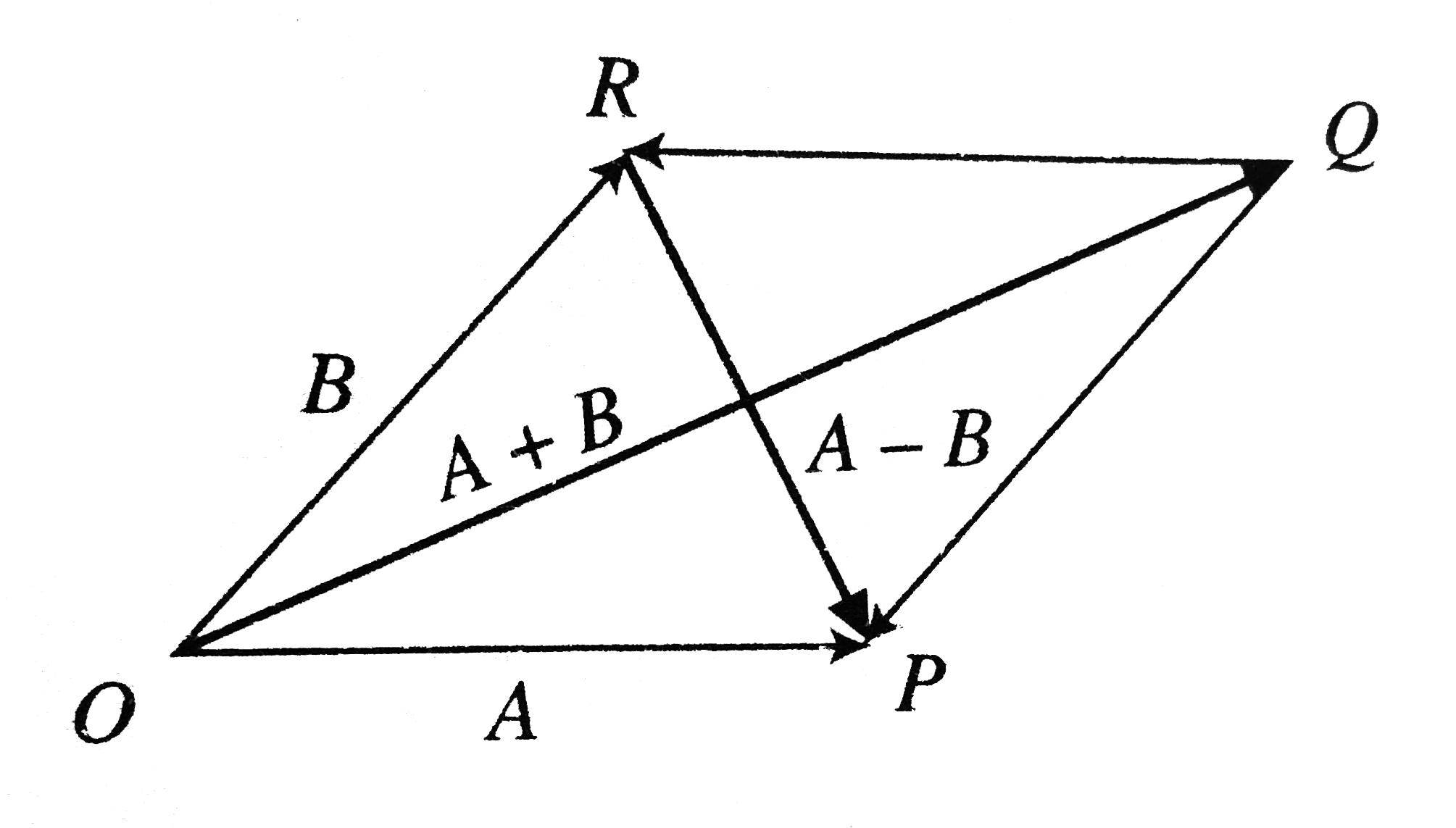
Since $- - \to O Q ⊥ - - \to R P, - - \to O Q . - - \to R P = 0,$ substituting $O Q = \to A + \to B$ and
$R P = \to A - \to B$ ,we have $(\to A + \to B) . (\to A - \to B) = 0$ .
This gives $\to A . \to A - \to A . \to B + \to B . \to A - \to B . \to B = 0$
since $\to A . \to A - {∣ ∣ \to A ∣ ∣}^{2}, \to B + \to B = {∣ ∣ \to B ∣ ∣}^{2}$ , and $\to A . \to B = \to B . \to A$ , we have
${∣ ∣ \to A ∣ ∣}^{2} - {∣ ∣ \to B ∣ ∣}^{2} 0 .$ Hence , $∣ ∣ \to A ∣ ∣ = ∣ ∣ \to B ∣ ∣ .$ It means that OP=OR.
This tells us that the given parallelogram is a rombus.

|

Updated on:21/07/2023

Class 11 PHYSICS VECTOR

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Diagonals of a parallelogram PQRS must be a
Arectangle
Bsquare
Ccyclic quadrilateral
Drhombus

CENGAGE PHYSICS-VECTORS-Exercise Multiple Correct

Home
Ask Doubt
Profile