Question

If the diagonals of a parallelogram are equal and intersect at right
angles, then the parallelogram is a square.

Explanation

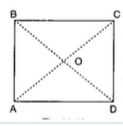
Consider a parallelogram ABCD
In ABCD the diagonals are AC and BD both intersect at right angle at O. So In triangle AOB and BOC
AO=OC (Diagonals are equal so half are also
So now in triangle ACB and ADC and `C=90^@`
`Angle AOB=Angle BOC (90^@)`
OB=OB(Common)
So by SAS Triangle AOB-BOC so AB=BC Similarly DOC and AOD Are also congruent so AD=DC
SO IF, AD=DC and AB=BC
So, We can conclude AD=AB also
AD=BC
Angle ADC-ABC(cpct)
AB=DC
SO IF ABC AND ADC ARE CONGRUENT so We can conclude that Angle A and B are equal
So If A=B,So `A+B=180`
`A+A=180` (Because both are equal)
`2A=180 A=180/2`
`A=90^@`
SO, B is also `90^@`
So If C=D
So `C+D=180^@`
`C+C= 180` (Because both are equal)
`2C=180`
`C=180/2`
So, D is also `90^@`
So all angle of square are `90^@` hence proved it is a square.