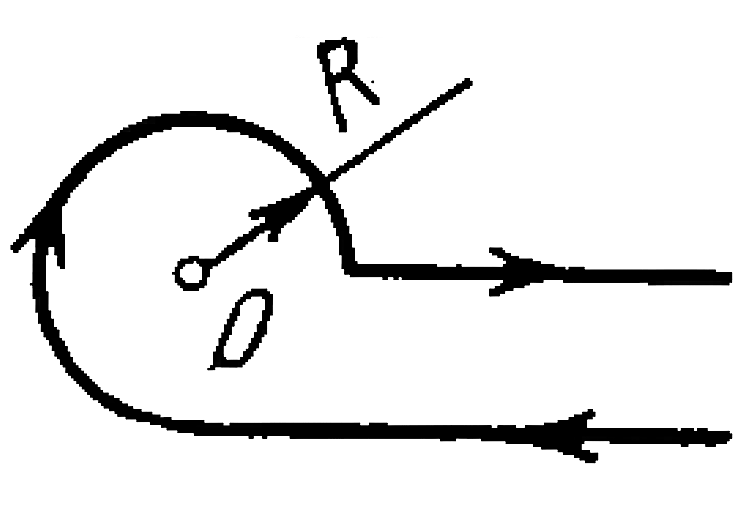
Calculate magnetic induction at point O if the wire carrying
a current I has the shape shown in Fig.
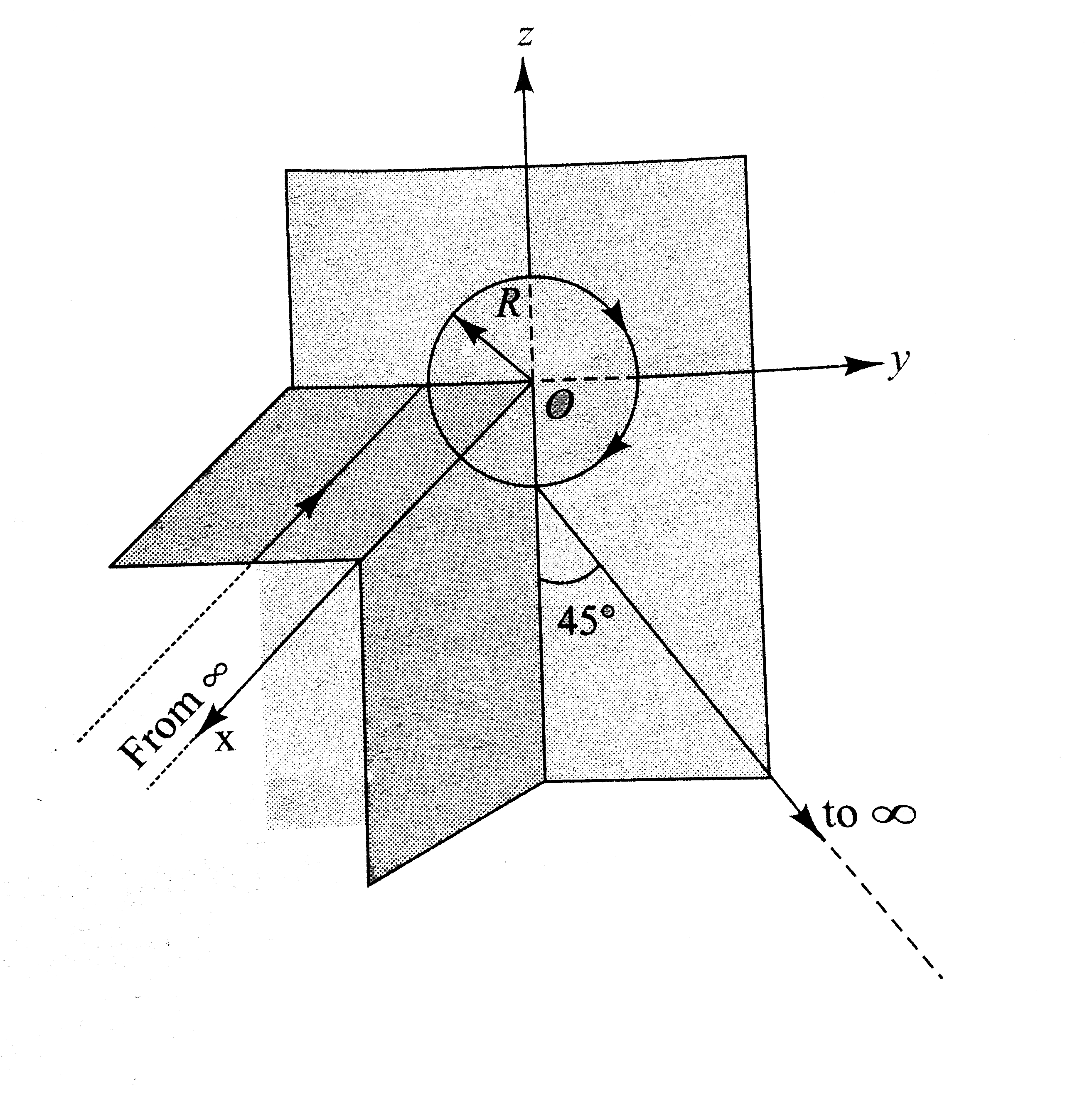
(The radius of the curved part of the wire is equal to R and linear parts of the wire are very long.)
The correct Answer is:−μ0I4R(√2−1)ˆi=μ0I8πRˆk
Circuit segment shown in fig. can be considered in three
parts.
(a) A circular loop in y-z plane. Since this loop is made of
uniform wire, therefore magnetic induction at O due to it is
B1=0.

(b) A straight part, parallel to x-axis. Magnetic induction due to
it is
B2=μ0I4πR(−ˆk)=−μ0I4πRˆk
(c) A straight part in y-z plane. Perpendicular distance of O
form axist of this straight part is r=Rcos45∘ as shown in figure.
Angles subtended by lines joining O and ends of this straight part with perpendicular drawn form O are α=45∘ and
β=90∘. Magnetic induction at O due to this part is
B3=μ0I4πR(sinα+sinβ)
→B3=μ0I4πR(√2−1)ˆi
→B=→B1+→B2+→B3=−μ0I4R(√2−1)ˆi−μ0I8πRˆk
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (single Correct )
Explore 75 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (multiple Currect )
Explore 5 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Concept Exercise 2.2
Explore 10 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:CENGAGE PHYSICSChapter:SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:QUESTION BANK
Explore 12 Videos
- THERMAL PROPERTIES OF MATTERBook:CENGAGE PHYSICSChapter:THERMAL PROPERTIES OF MATTERExercise:Question Bank
Explore 40 Videos
Similar Questions
Find the magnetic induction at the point O if the wire carrying a current I=8.0A has the shwon in Fig.
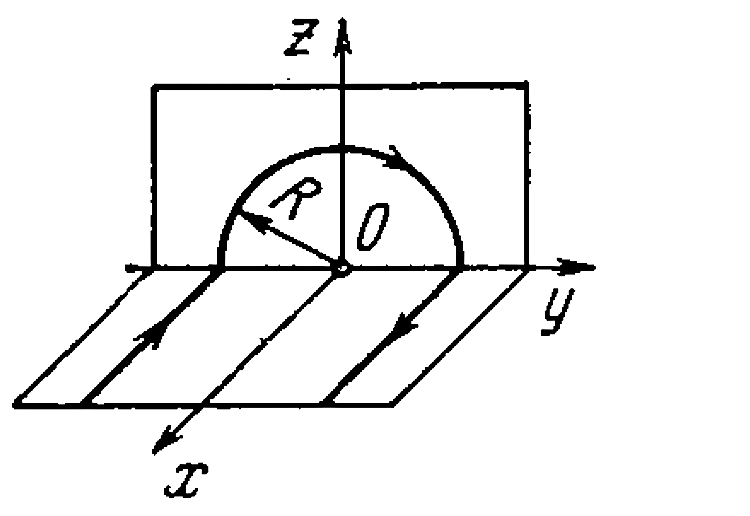
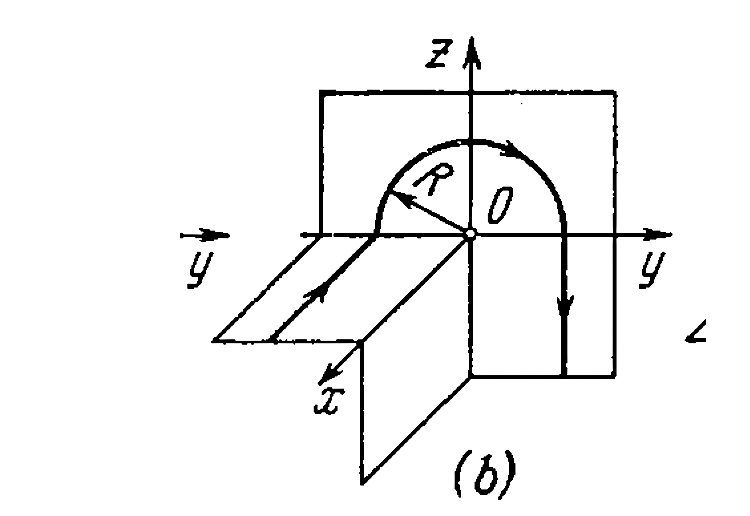
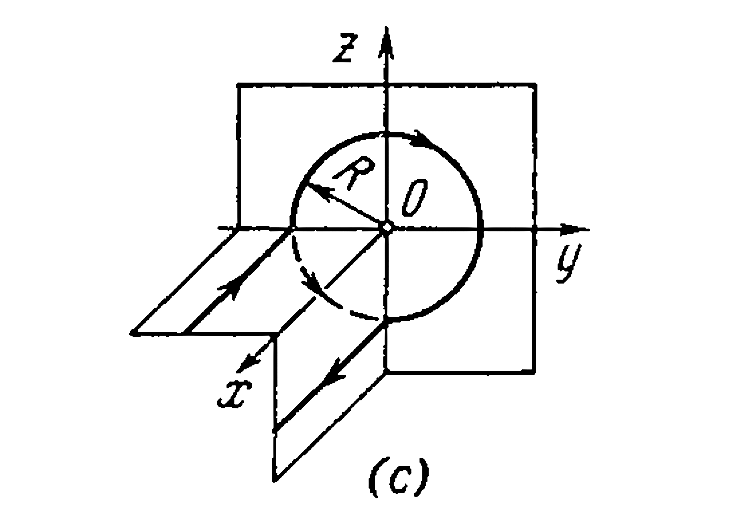
The radius of the curved part of the wire is R=100mm, the linear parts of the wire are very long.
View SolutionFind the magnetic field induction at a point O if the wire carrying current I=8⋅0A has a shape as shown in figure. The radius of the curved path of the other wire is r=100mm and linear paths of wire are very long.

View Solution
Knowledge Check
The magneticl induction at the point O, if the wire carries a current I, is
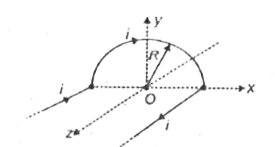 Aμ0i2RBμ0i2πRCμ0i(π2+4)1/24πRDμ0i(π2+4)4πR
Aμ0i2RBμ0i2πRCμ0i(π2+4)1/24πRDμ0i(π2+4)4πRFind the magnetic induction at point O, if the current carrying wire is in the shape shown in the figure.
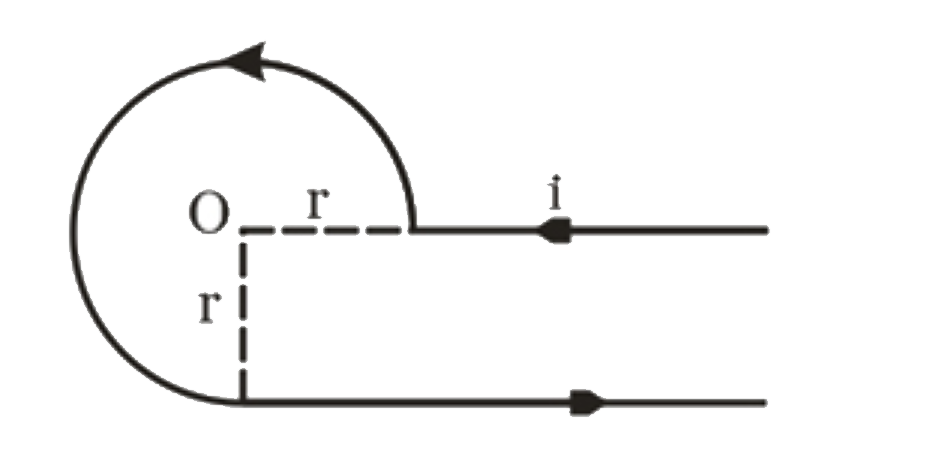 Aμ0l5πr[3π2+1]⊙Bμ0l3πr[3π4+1]⊙Cμ0l2πr[3π4+1]⊙Dμ0l4πr[3π2+1]⊙
Aμ0l5πr[3π2+1]⊙Bμ0l3πr[3π4+1]⊙Cμ0l2πr[3π4+1]⊙Dμ0l4πr[3π2+1]⊙The magnetic induction at any point due to a long straight wire carrying a current is
AProportional to the distance from the wireBInversely proportional to the distance from wireCInversely proportional to the square of the distance from the wireDDoes not depend on distance
(a) Find the magnetic field at the point O if the wire carrying a current i has the shape shown. The radius of the current part of the wire is R, the linear parts of the wire are very long.
(i)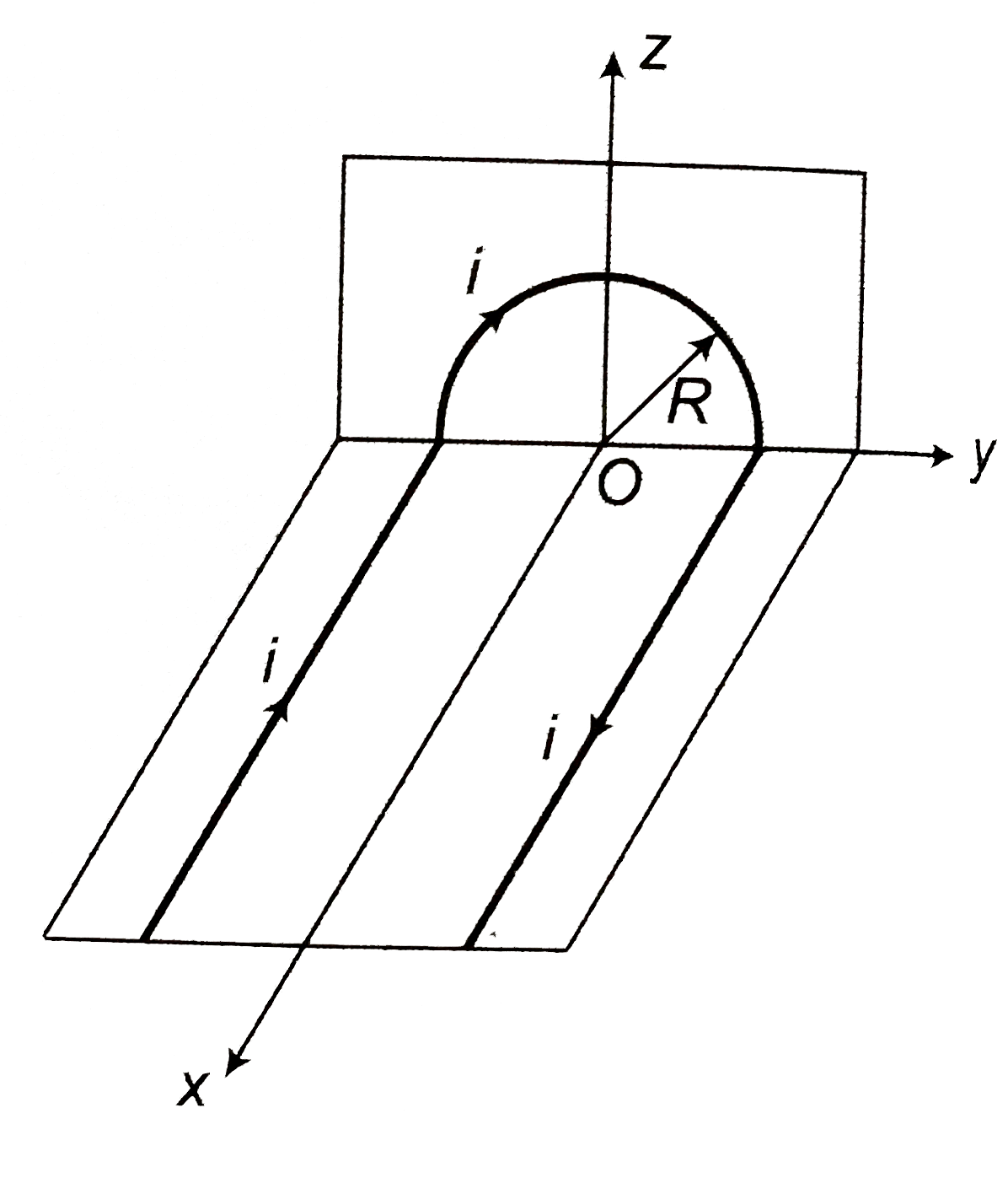
(ii)
(iii)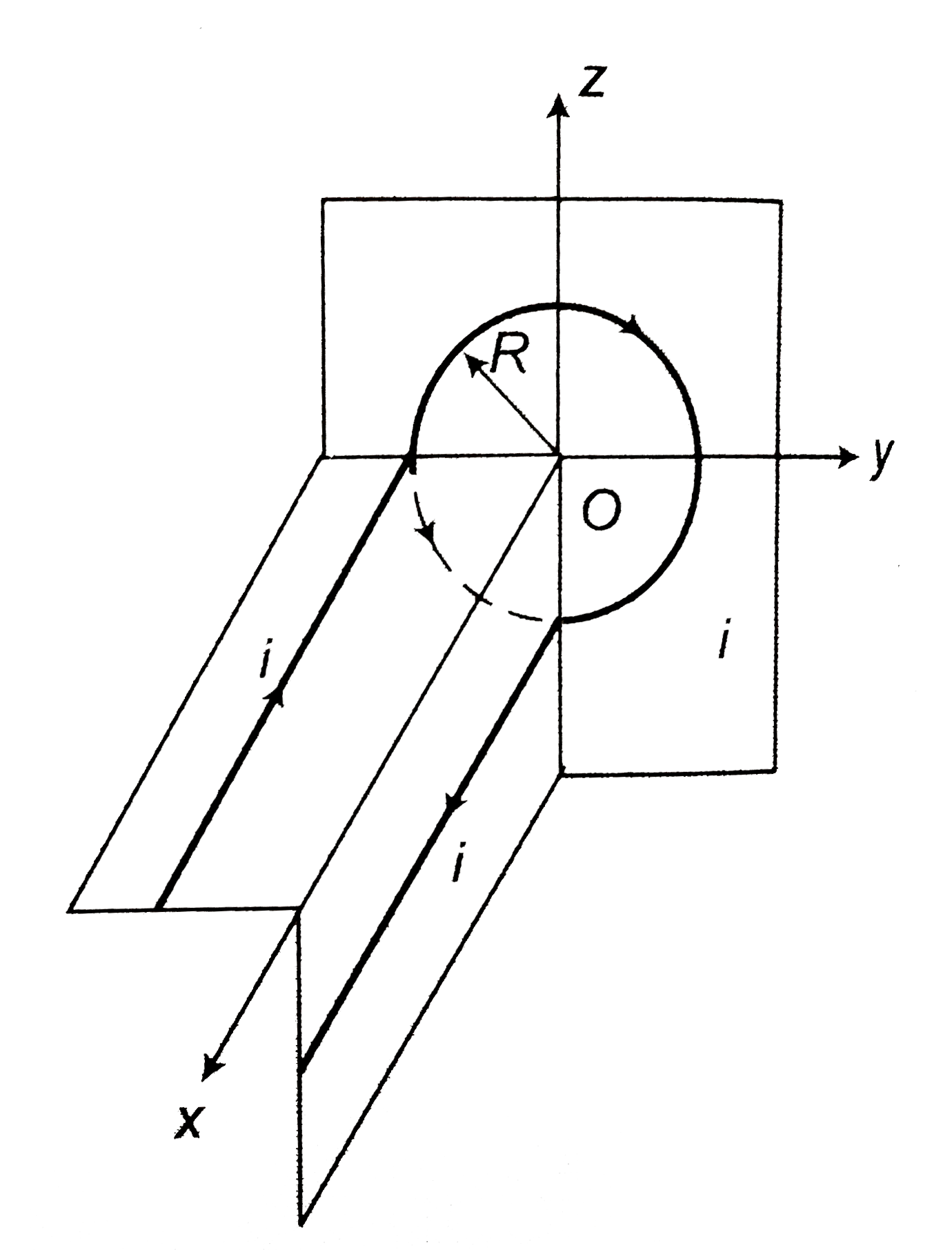
(b) A long straight wire along the z-axis carriers a current i in negative z-direction. Find magnetic field in vector from at a point having co-ordinates (x,y) on z=0 plane.
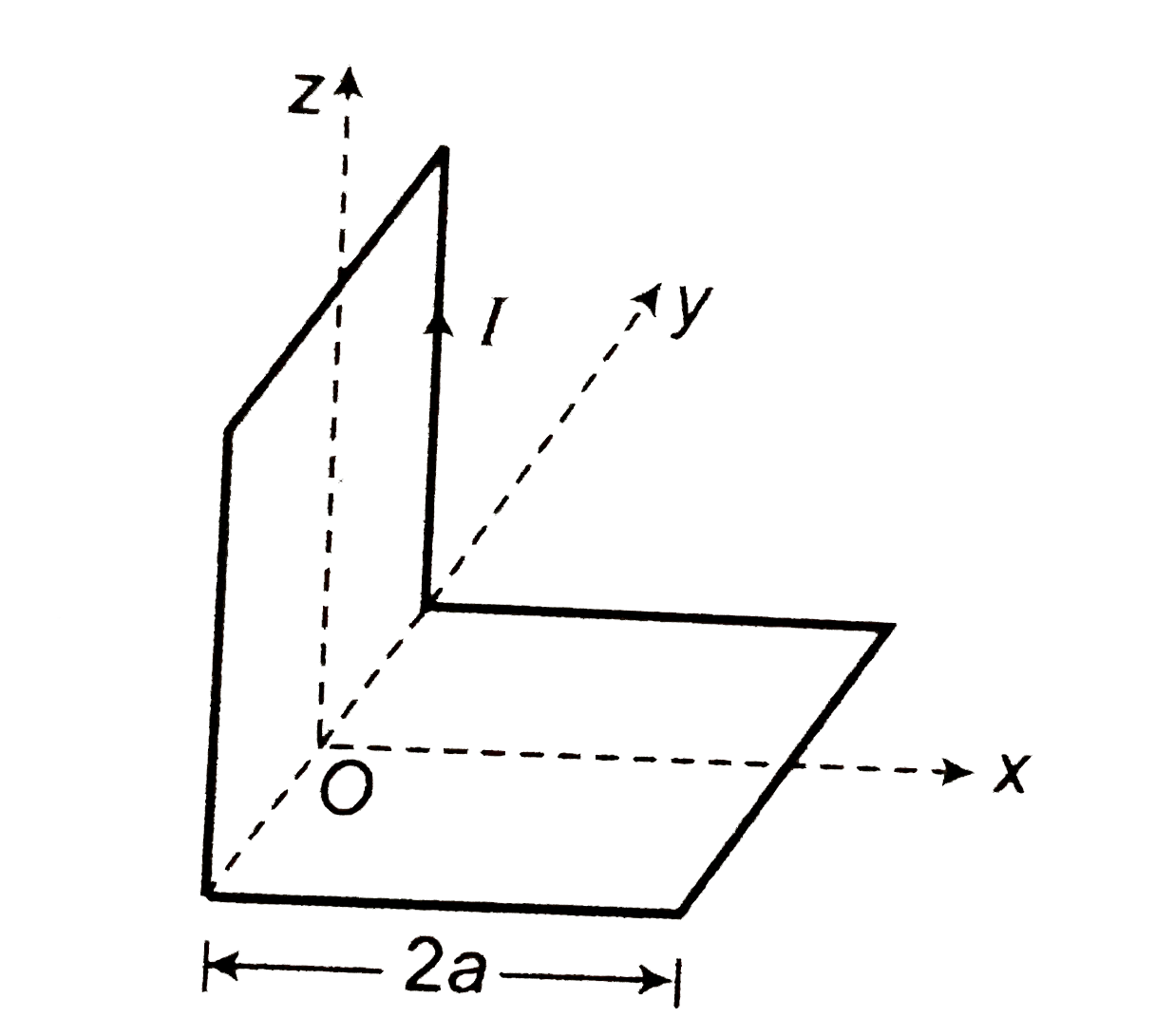
(c) A non-coplaner loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop of length 2a. find unit vector along magnetic field magnetic filed at the point P(a,0,a).
View SolutionFind the magnetic induction at the point O of the following figures if the wire carrying a current I = 15A has the shapes shown here. The radius of the curved part R=5cm, the linear parts of the wire are very long.
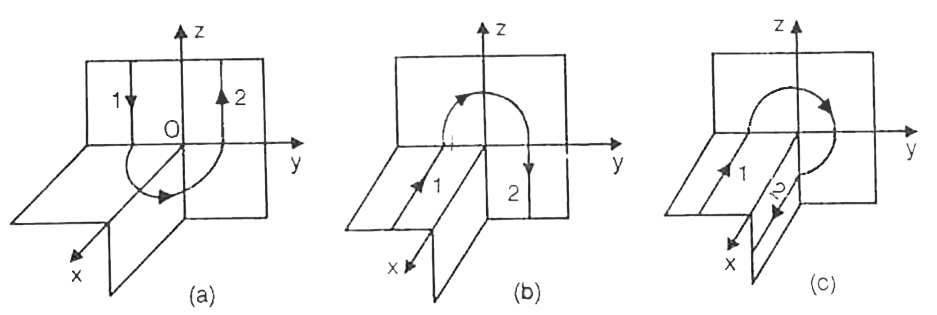
View SolutionFind the magnetic induction at point O, if the current carrying wire is in the shape shown in the figure
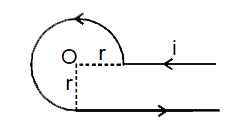
View SolutionFind the magnetic induction at point O if the current carrying wire is in the shape shown in the figure.
 .
.
View SolutionFind the magentic induction of the field at the pont O if a current-carrying wire has the shape shown in Figa,b,c The raidius of the curved part of the of the weir is R the linear parts are assumed to be very long.
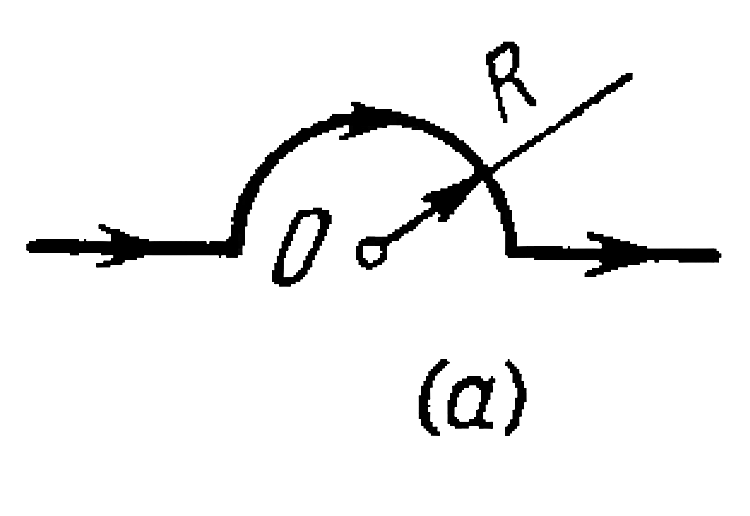

View Solution