Two long conducting rods suspended by means of two insulating threads as shown in Fig. are connected at one end to a charged capacitor through a switch S, which initially open. At the other end , they are connected by a loose wire. The capacitor has charge Q and mass per unit length of the rod is λ. The effective resistance of the circuit after closing the switch is R. Find the velocity of each rod when the capacitor is discharged after closing the switch. (Assume that the displacement of rods during the discharging time is negligible.)

The correct Answer is:μ0Q24πdRCλl
Fmag=ma
μ0I22πd=λla(where l=length of each rod)
μ02πd(QRCe−tRC)2=λldvdt
μ02πd×Q2(RC)2×∫∞0e−2tRCdt=λl=∫v0dv
μ0Q22πdRC.2=λlv⇒v=μ0Q24πdRCλl
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (single Correct )75videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )5videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.210videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK12videos
SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank40videos
THERMAL PROPERTIES OF MATTER
Similar Questions
In the circuit shown in figure, the capacitors are initially uncharged. The current through resistor PQ just after closing the switch is
 View Solution
View SolutionConisder the istuation shown in the figure. The capacitor A has a charge q on it whereas B is unchanged. The charge appearing on the capacitor B a long time after the switch is closed is
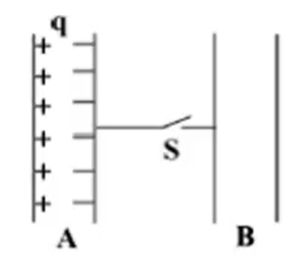 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the given figure switch is open initially and capacitor C2 is unchanged
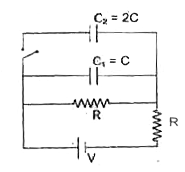
Charge on C2 just after closing the switch isACV2BCV3CCV4DCV8 - Question 2 - Select One
In the circuit shown in fig. when the switch is closed, the capacitor charges with a time constant
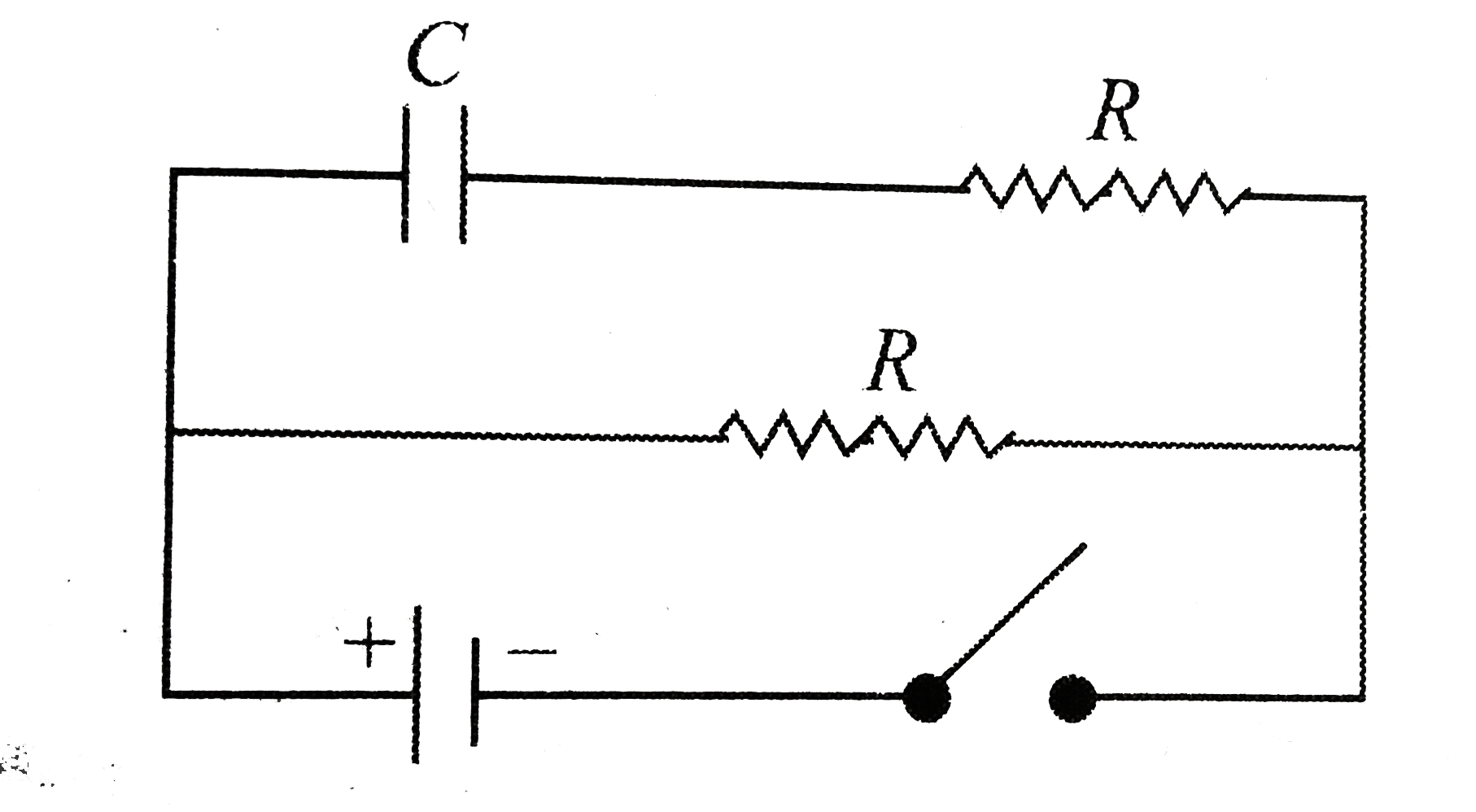 ARCB2 RCC12RCDRC log2
ARCB2 RCC12RCDRC log2 - Question 3 - Select One
In the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
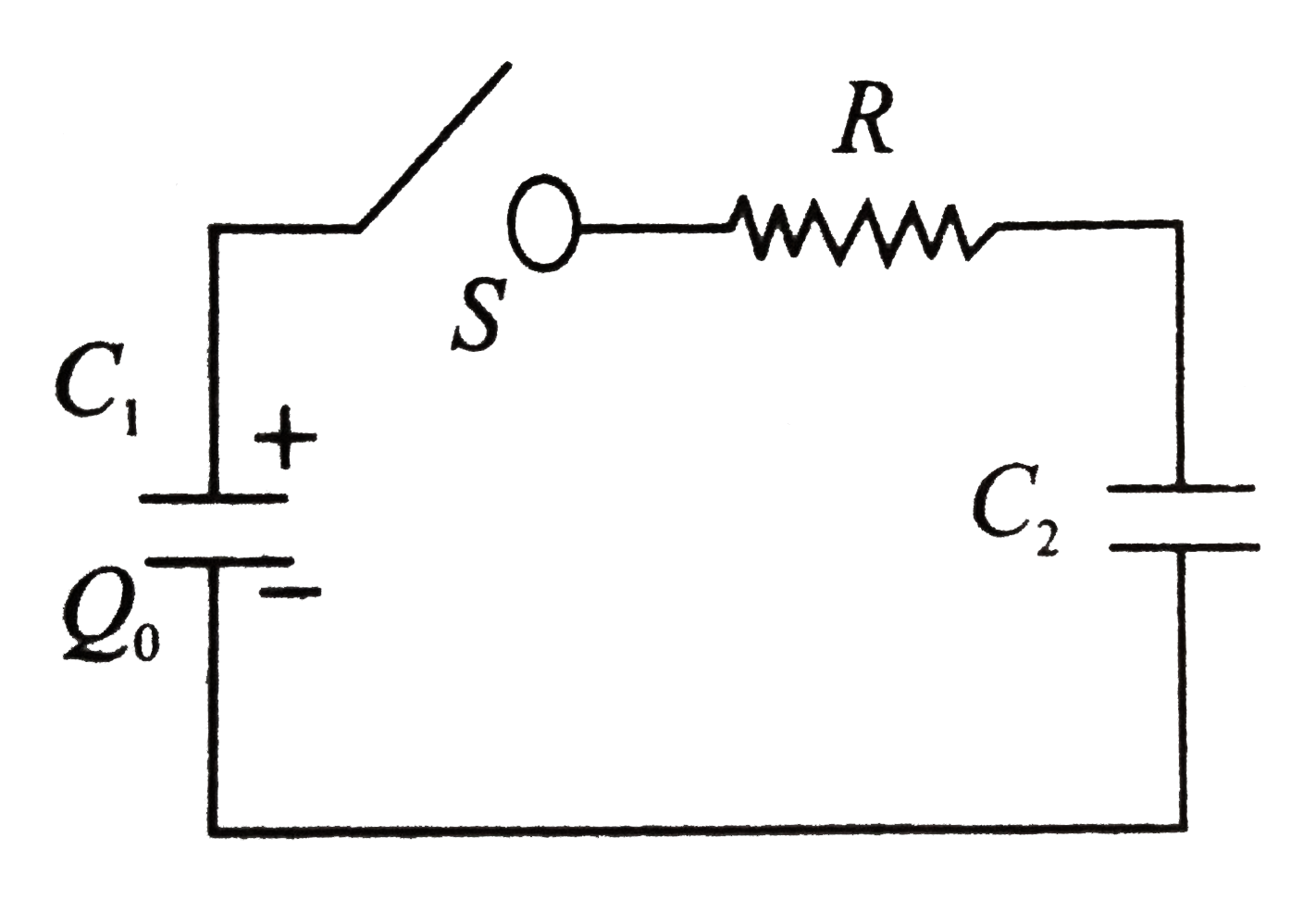 Aq0C1C1+C2(1−e−t(C1+C2)C1C2R)Bq0C2C1+C2(1−e−t(C1+C2)C1C2R)Cq0C1C1+C2(1−e−tC2R)Dq0C2C1+C2(1−e−tC2R)
Aq0C1C1+C2(1−e−t(C1+C2)C1C2R)Bq0C2C1+C2(1−e−t(C1+C2)C1C2R)Cq0C1C1+C2(1−e−tC2R)Dq0C2C1+C2(1−e−tC2R)
In the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant
 View Solution
View Solution
In the circuit shown, all the capacitors are initially uncharged. The current through the battery just after closing the switch 'S' isView SolutionThe circuit was in the shown state for a long time. Now if the switch S is closed then the net charge that flows through the switch S, will be
 View Solution
View SolutionIn the given LC circuit if initially capacitor C has change Q on it and 2C has charge 2Q. The polarities are as shown in the figure. Then after closing the switch s at t=0
 View Solution
View SolutionConsider the situation shown in the figure. The capacitor A has a charge q on it whereas B is uncharged. The charge appearing on the capacitor B a long 7 time after the switch is closed is :
 .View Solution
.View Solution

