Calculate moment of inertia of a uniform circular disc of mass 700g and diameter 20cm about
(i) an axis through the centre of disc and perpendicular to its plane, (ii) a diameter of disc, (iii) a tangent in the plane of the disc, (iv) a tangent perpendicular to the plane of the disc.
Here, M=700g,R=202cm=10cm
(i) I=12MR2=12×700×102=3.5×104gcm2
(ii) I=14MR2=14×700×102
=1.75×104gcm2
(iii) I=54MR2=54×700×102
=8.75×104gcm2
(iv) I=32MR2=32×700×102
=1.05×105gcm2
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS FOR PRACTICE TYPE B
2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS FOR PRACTICE TYPE C
2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS FOR PRACTICE TYPE A
2 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
Calculate the moment of inertia of uniform circular disc of mass 500 g, radius 10 cm about : the axis through the centre of the disc and perpendicular to its plane
View SolutionCalculate moment of inertia of a uniform circular disc of mass 10kg and diameter 0.5m about a tangent perpendicular to the plane of the disc.
View Solution
Knowledge Check
Moment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
AMR22−M(4R3π)2BMR22−M(√24R3π)2CMR22+M(4R3π)2DMR22+M(√24R3π)2If a circular concentric hole is made on a disc then about an axis passing through the centre of the disc and perpendicular to its plane
Amoment of inertia decreasesBmoment of inertia increasesCradius of gyration increasesDradius of gyration decreasesThe moment of inertia of a uniform semicircular disc of mass disc through the centre is
A25Mr2B14Mr2C12Mr2DMr2
Calculate the moment of inertia of uniform circular disc of mass 500 g, radius 10 cm about : diameter of the disc
View SolutionCalculate the moment of inertia of uniform circular disc of mass 500 g, radius 10 cm about : the axis tangent to the disc and parallel to its diameter
View SolutionCalculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionThe moment of inertia of a uniform cicrular disc about its diameter is 200gcm2. Its moment of inertia about an axis passing through its centre and perpendicular to its circular face is
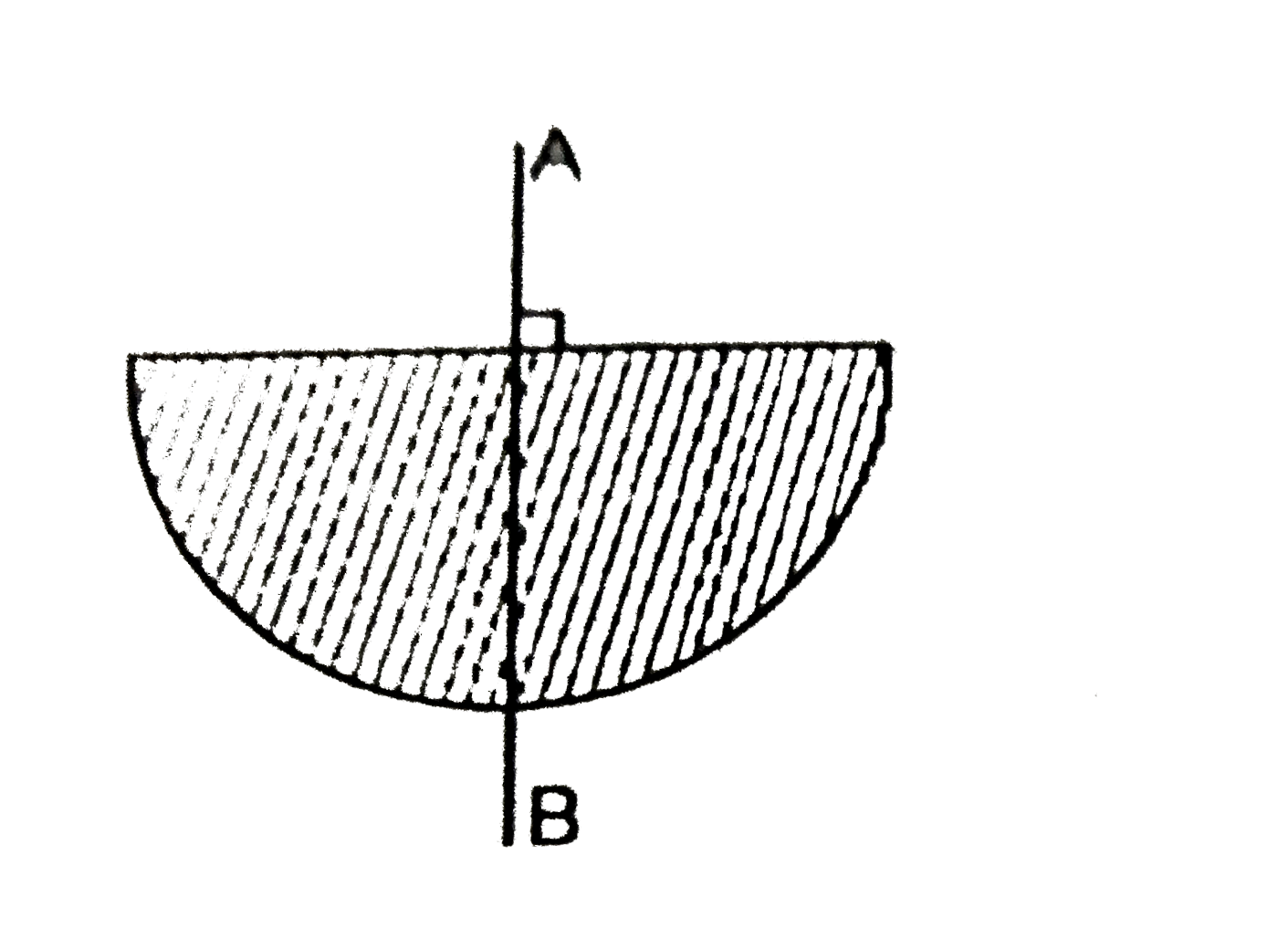
View SolutionA uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
View Solution
