Calculate the angular frequency of the system shown in figure. Friction is absent everywhere and the threads, spring and pulleys are mass-less. Given that mA=mB=m.

The correct Answer is:A, B, D
Let x0 be the extension in the spring in equilibrium. Then equilibrium of A and B give,
T=kx0+mgsinθ …(i)
and 2T=mg …(ii)
Here, T is the tension in the string. Now, suppose A is further displaced by x2 and speed of B at this instant will be v2. Total energy of the system in this position will be,
E=12k(x+x0)2+12mAv2+12mB(v2)2+mAghA−m(B)ghB
or E=12k(x+x0)2+12mv2+18mv2+mgxsinθ−mgx2
or E=12k(x+x0)2+58mv2+mgxsinθ−mgx2
Since, E is contant,
dEdt=0
or 0=k(x+x0)dxdt+54mv(dvdt)+mg(sinθ)(dxdt)−mg2(dxdt)
Substituting, dxdt=v rArr dvdt=a
and kx0+mgsinθ=mg2
[From Eqs. (i)and(ii)]
We get, 54ma=−kx
Since, a∝−x
Motion is simple harmonic, time period of which is,
T=2π√∣∣xa∣∣
=2π√5m4k
∴ω=2πT=√4k5m
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Assertion And Reason
10 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 13
3 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Calculate the angular frequency of the system shown in figure. Friction is absent everywhere and the threads, spring and pulleys are mass-less. Given that mA=mB=m.

View SolutionFriction is absent everywhere and the threads, spring and pulleys are massless. If mA=mB=M, then the angular frequency of the system for small oscillations will be

View Solution
Knowledge Check
Calculate the angular frequency of the system shown in figure. Friction is absent everywhere and the threads, spring and pulleys are massless. Given that mA=mB=m.
 A√2k4mB√4k5mC√6k7mD√8k5m
A√2k4mB√4k5mC√6k7mD√8k5mTwo blocks A and B of equal mass m are connected through a massless string and arranged as shown in the figure. Friction is absent everywhere. When the system is released from rest
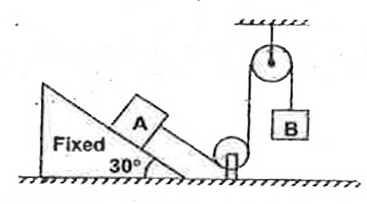 Atension in the string is mg2Btension in the string is mg4Cacceleration of A is g2Dacceleration of A is 3g4
Atension in the string is mg2Btension in the string is mg4Cacceleration of A is g2Dacceleration of A is 3g4In the system shown in figure m1>m2. System is held at rest by thread BP. Just after the thread BP is burnt :
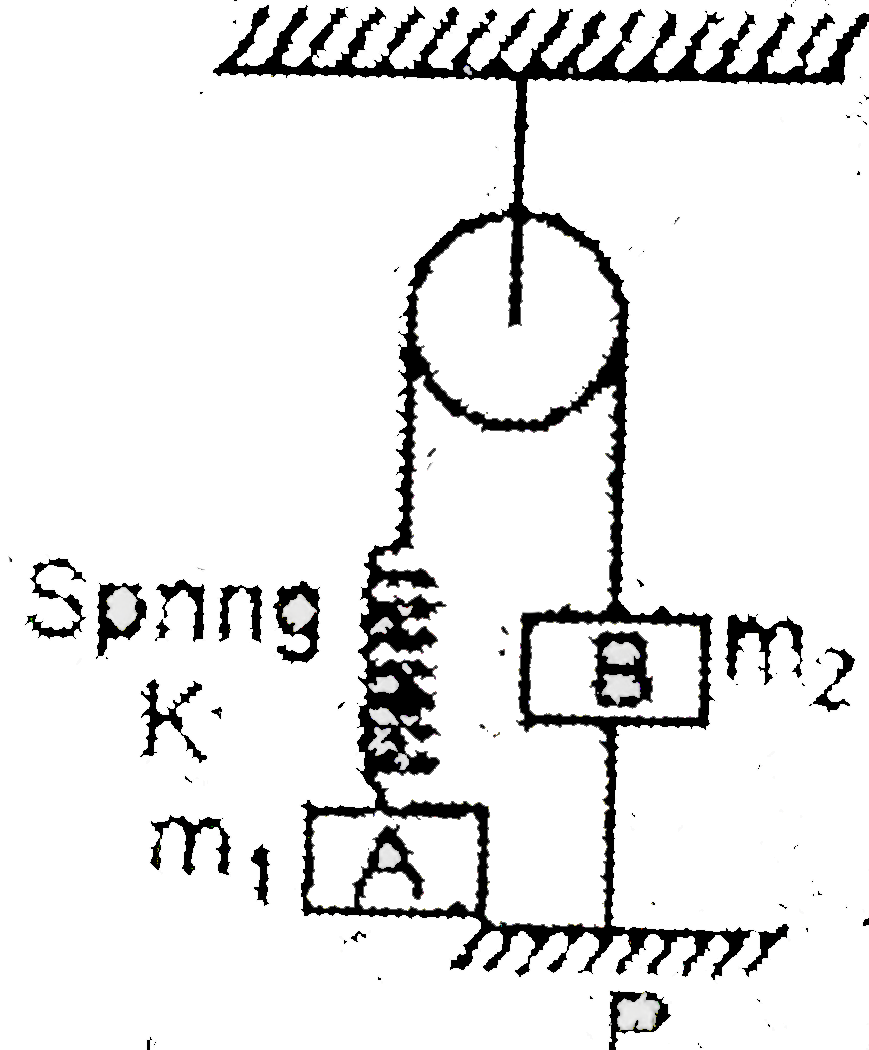 AMagnitude of acceleration of both blocks will be equal to (m1−m2m1+2m2)gBAcceleration of m1 will be equal to zeroCAcceleration of m2 will be upwardsDMagnitudes of acceleration of two blocks will be non-zero and unequal
AMagnitude of acceleration of both blocks will be equal to (m1−m2m1+2m2)gBAcceleration of m1 will be equal to zeroCAcceleration of m2 will be upwardsDMagnitudes of acceleration of two blocks will be non-zero and unequal
A uniform circular chain of radius r and mass m rests over a sphere of radius R as shown in figure. Friction is absent everywhere and system is in equilibrium . Find the tension in the chain.
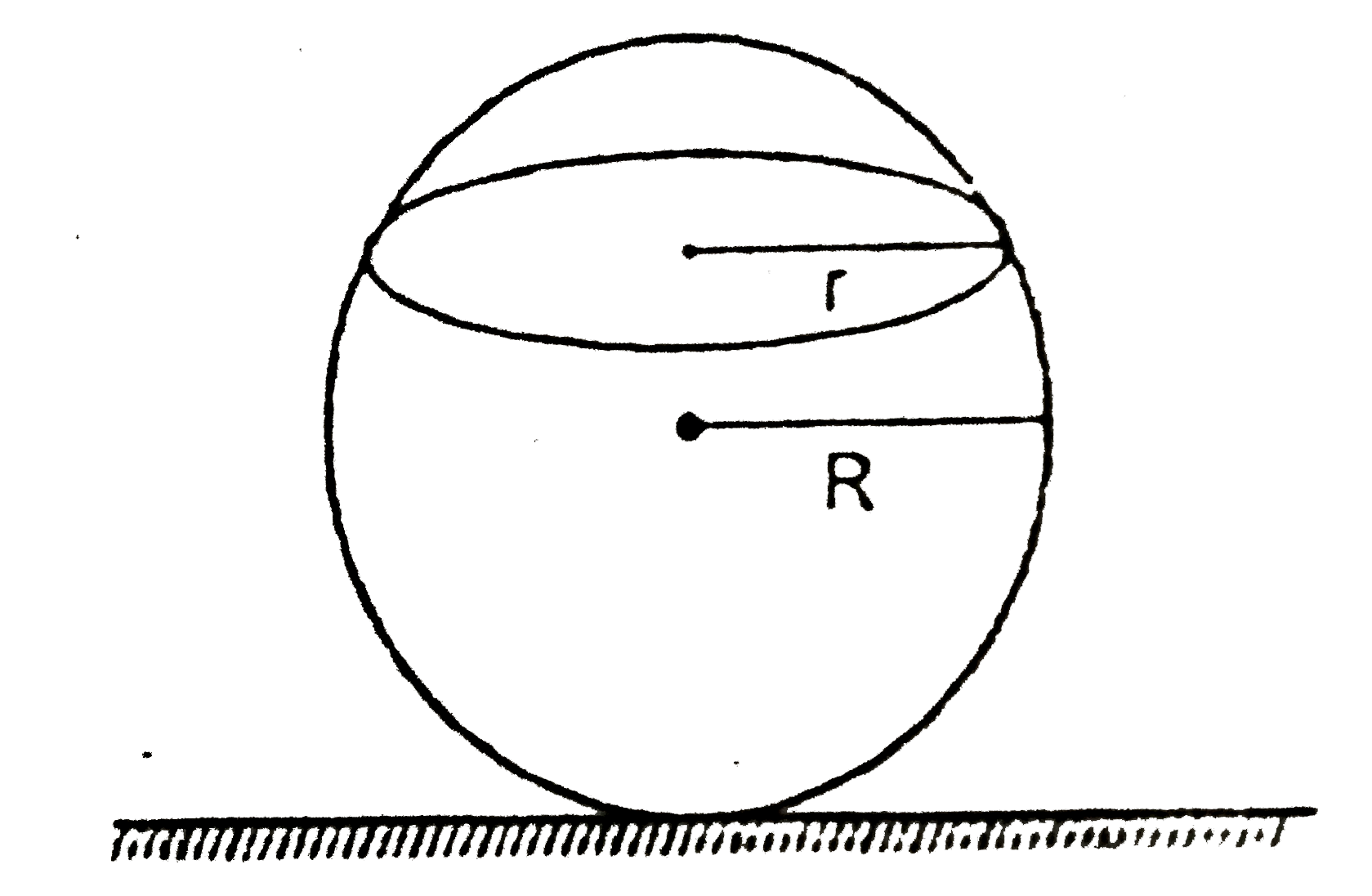
View SolutionFind the natural frequency of the system as shown in the figure. The pulleys are massless and frictionless.
(Take k=9π2N/m and m=4kg)

View SolutionA block of mass m slides down on inclined wedge of same mass m as shown in figure . Friction is absent everywhere . Acceleration of centre of mass of the block and wedge is
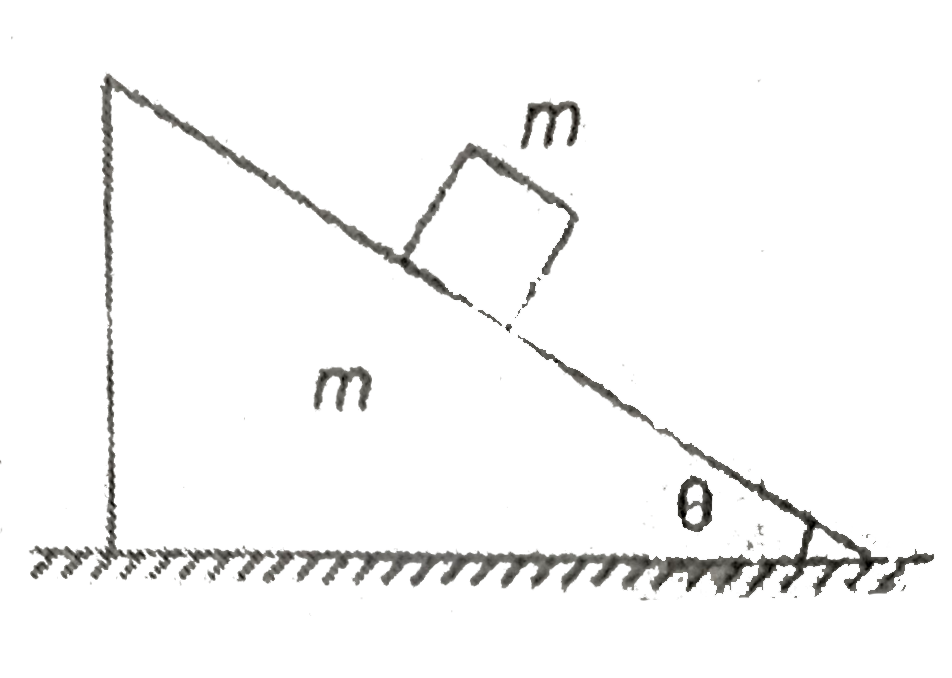
View SolutionFind the stretch in the springs shown in figure-2.112. The respective data are given in the figure. The friction and masses in pulleys are negligible.
View SolutionThe string, spring and the pulley shown in figure are light. Find the time period of the mass m.

View Solution
