Calculate the area enclosed under the curve f(x)=x2 between the limits x=2 and x=3 (figure)
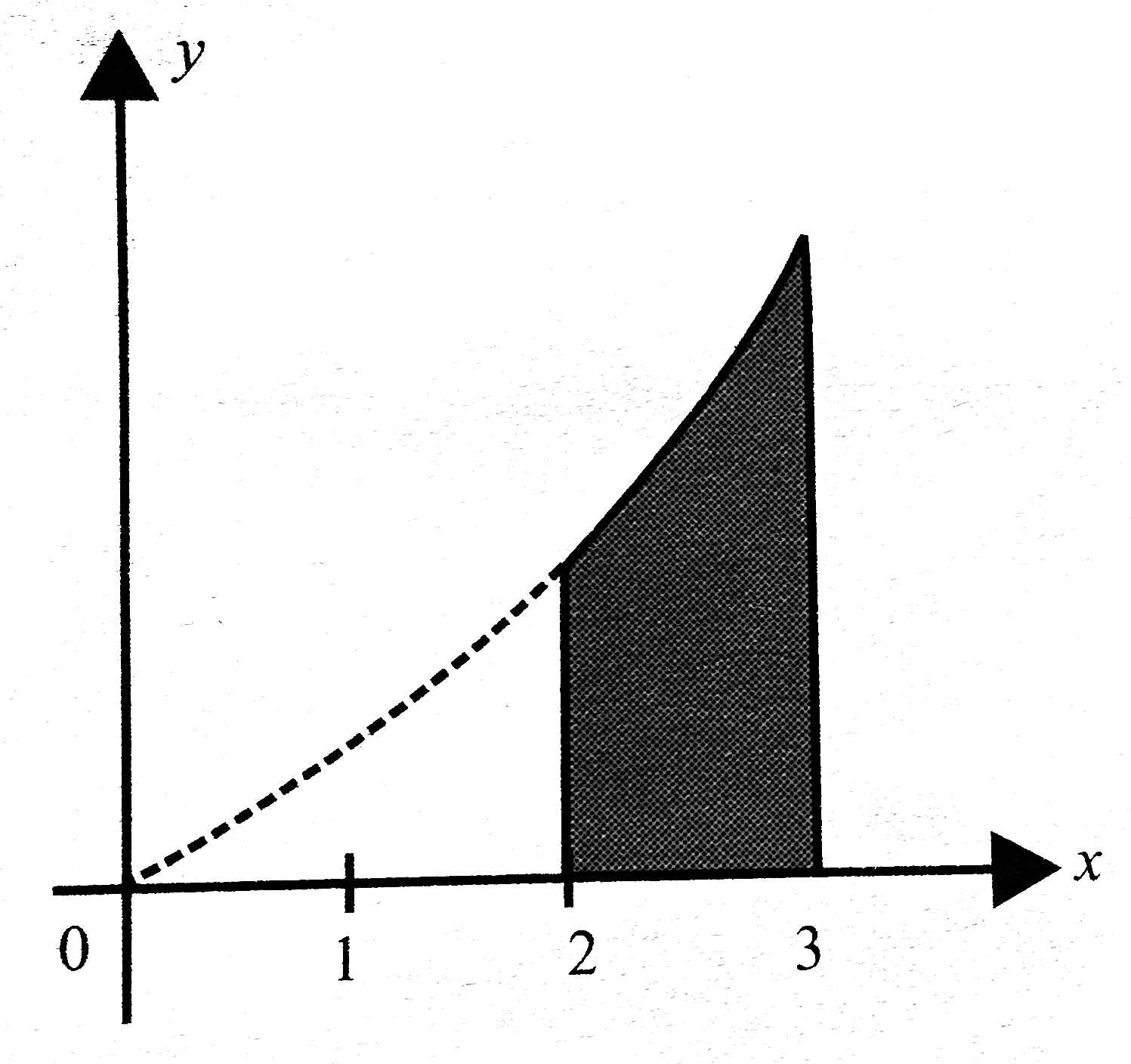
Video Solution
Text Solution
3∫2f(x)dx=3∫2x2dx
=x33∣∣∣32
=(3)33−(2)33=193=6.333
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Solved Examples9videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.12videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ARCHIVES 2 VOLUME 6EXERCISE - Integer4videos
ARCHIVES 2 VOLUME 6
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
Similar Questions
The area enclosed by the curve y2+x4=x2 is
View SolutionCalculate the area under the curve y=2√x included between the lines x = 0 and x = 1.
View SolutionFind the area under the curve y=(x2+2)2+2x between the ordinates x =0 and x=2
View SolutionThe area enclosed within the curve |x|+|y|=1 is
View SolutionFind the area enclosed with in the curve
y2=3x,x=3View SolutionFind the area enclosed by the curves x^2=y , y=x+2,
View SolutionFind the area enclosed by the curves y=4x2 and y2=2x.
View SolutionCalculate the area enclosed by the curve 4≤x2+y2≤2(|x|+|y|).
View SolutionFind the area enclosed by the curve y=−x2 and straight line x+y+2=0.
View SolutionFind the area under the curve y=sin2x+cos2x between the ordinates x = 0, x=π4
View Solution

