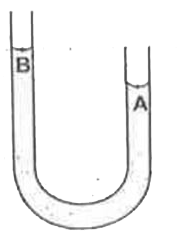
Calculate the difference $h$ in water levels in two commnicating capillary tube of radius $1 m m$ and $1.5 m m$ . Surface tension of water $= 0.07 N m^{- 1}$

Video Solution

Text Solution

Verified by Experts

Pressure at $A = p_{0} + \frac{2 T}{r_{1}}$
(since pressure on concave side is greater than that on convex side)
Pressure at $B = p_{0} - \frac{2 T}{r_{2}}$
Therefore, pressure difference $= 2 T (\frac{1}{r_{1}} - \frac{1}{r_{2}})$
Let this pressure difference correspond to $h$ units of the liquid. Then
$2 T (\frac{1}{r_{1}} - \frac{1}{r_{2}}) = ρ g h \Rightarrow h = \frac{2 T}{ρ g} (\frac{1}{r_{1}} - \frac{1}{r_{2}})$
$∴ h = \frac{2 \times 0.07}{1000 \times 9.8} (\frac{1}{1 \times 10^{- 3}} - \frac{1}{1.5 \times 10^{- 3}}) = 4.76 m m$

|

Updated on:21/07/2023

Class 11 PHYSICS PROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Water rises in a capillary tube of diameter $0.2 \times 10^{2} m$ upto a height of 1.5 cm. The surface tension of water is-
A $73.5 \times 10^{1} N / m$
B $73.5 \times 10^{- 3} d y ne / c m$
C $35.7 \times 10^{- 3} N / m$
D $43.5 \times 10^{- 3}$
Question 2 - Select One
What will be the difference of pressure inside and outside a drop of water of radius 1.0 mm ? (The surface tension of water is 73 dyne/cm-)
A $146 N / m^{2}$
B $73 N / m^{2}$
C $7.3 N / m^{2}$
D $200 N / m^{2}$
Question 3 - Select One
The rise in the water level in a capillary tube of radius 0.07 cm when dipped vertically in a beaker containing water of surface tension $0.07 N m^{- 1}$ is (g = $10 m s^{- 2}$ )
A2 cm
B4 cm
C1.5 cm
D3 cm

CENGAGE PHYSICS-PROPERTIES OF SOLIDS AND FLUIDS-INTEGER_TYPE

Home
Ask Doubt
Profile