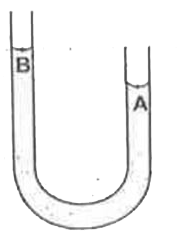
The difference in water levels in the two communicating capillary tubes of different diameter d = 1 mm and d = $1.5$ mm is $K \times 2.38$ .Surface tension of water = $0.07$ N/m and angle of contact between glass and water is $0^{\circ}$ .Find the value of K .

Video Solution

Text Solution

Verified by Experts

$2 T cos θ (\frac{1}{r_{1}} - \frac{1}{r_{2}}) - ρ g h$
$K = 2$

Updated on:21/07/2023

Water rises in a capillary tube of diameter $0.2 \times 10^{2} m$ upto a height of 1.5 cm. The surface tension of water is-
A $73.5 \times 10^{1} N / m$
B $73.5 \times 10^{- 3} d y ne / c m$
C $35.7 \times 10^{- 3} N / m$
D $43.5 \times 10^{- 3}$
A capillary tube of 2mm diameter. What is the height to which water rises, if surface tension of water is $7.4 \times 10^{- 9} N m^{- 1}$ and angle of contact is $0^{\circ}$ ?
A0.25mm
B1.51mm
C0.4mm
D0.5mm
A long capillary tube of radius $0.2 m m$ is placed vertically inside a beaker of water.
If the surface tension of water is $7.2 \times 10^{- 2} N / m$ the angle of contact between glass and water is zero, then determine the height of the water column in the tube.
A $3 c m$
B $9 c m$
C $7 c m$
D $5 c m$