Calculate the discharge in litres per minute of a venturi-meter if it is of 86 cm diameter in main part and of 10 cm diameter in neck part. Specific gravity of Hg=13.6 and difference of pressure of water between mains and neck is 20 cm of Hg.
To calculate the discharge in litres per minute of a Venturi-meter with given diameters and pressure difference, we will follow these steps:
Step 1: Convert the pressure difference from cm of Hg to meters of water.
The pressure difference is given as 20 cm of Hg. We can convert this to meters of water using the specific gravity of mercury (Hg).
H=Pressure difference=20cm Hg=20×13.6×10−2m of water
Calculating this gives:
H=20×13.6×0.01=2.72m of water
Step 2: Calculate the cross-sectional areas A1 and A2.
The cross-sectional area of the main part (section 1) and the neck part (section 2) can be calculated using the formula:
A=πD24
For A1 (main part, diameter D1=86cm=0.86m):
A1=π(0.86)24=π×0.73964≈0.580m2
For A2 (neck part, diameter D2=10cm=0.10m):
A2=π(0.10)24=π×0.014≈0.00785m2
Step 3: Use the discharge formula for the Venturi-meter.
The discharge Q can be calculated using the formula:
Q=A1A2√2gHA21−A22
Where g is the acceleration due to gravity (approximately 10m/s2).
Substituting the values we have:
Q=0.580×0.00785×√2×10×2.72(0.580)2−(0.00785)2
Calculating the denominator:
(0.580)2−(0.00785)2≈0.3364−0.0000616225≈0.3363383775
Now substituting this back into the discharge equation:
Q≈0.580×0.00785×√54.40.3363383775
Calculating the square root:
√54.40.3363383775≈√161.0≈12.688
Now substituting this value back into the equation for Q:
Q≈0.580×0.00785×12.688≈0.051m3/s
Step 4: Convert the discharge from m³/s to litres/minute.
To convert cubic meters per second to litres per minute:
Q=0.051m3/s×1000litres/m3×60s/min=3060litres/min
Final Answer:
The discharge of the Venturi-meter is approximately 3060 litres per minute.
---
The pressure difference is given as 20 cm of Hg. We can convert this to meters of water using the specific gravity of mercury (Hg).
H=20×13.6×0.01=2.72m of water
The cross-sectional area of the main part (section 1) and the neck part (section 2) can be calculated using the formula:
A=πD24
A1=π(0.86)24=π×0.73964≈0.580m2
A2=π(0.10)24=π×0.014≈0.00785m2
The discharge Q can be calculated using the formula:
Q=A1A2√2gHA21−A22
Q=0.580×0.00785×√2×10×2.72(0.580)2−(0.00785)2
(0.580)2−(0.00785)2≈0.3364−0.0000616225≈0.3363383775
Q≈0.580×0.00785×√54.40.3363383775
√54.40.3363383775≈√161.0≈12.688
Q≈0.580×0.00785×12.688≈0.051m3/s
To convert cubic meters per second to litres per minute:
Q=0.051m3/s×1000litres/m3×60s/min=3060litres/min
The discharge of the Venturi-meter is approximately 3060 litres per minute.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (A. MCQ (Objectie Type Questions))
20 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (B. MCQ (AIPMT/NEET & Other State Boards For Medical Entrance))
6 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Long Answer Questions)
7 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
A venturimeter is 37.5cm. Diameter in mains and 15cm. Diameter in throat. The difference between the pressure of water in the mais and the throat is 23cm of Hg. Find the discharge in litres/minunte. Sp. Gravity of Hg. 13.56.
View SolutionCalculate the mass of water flowing in 10 minutes throuth a tube 1 mm in diameter and 0.40 m long ,if there is a constant pressure heat of 20 cm of water . Coefficient of visosity of water is 0.00089 Pas.
View Solution
Knowledge Check
Water is conveyed throuh a uniform tube of 8 cm in diameter and 3140 m in length at the rate 2×10−3m3 per second. The pressure required to maintain the flow is ( viscosity of water =10−3 )
A6.25×103Nm−2B0.625Nm−2C0.0625Nm−2D0.00625Nm−2
Water rises to a height of 9 cm in a certain capillary tube. If in the same tube, level of Hg is depressed by 3cm compare the surface tension of water and mercury. Specific gravity of Hg is 13.6, the angle of contact for water is zero and that for Hg is 135∘.
View SolutionA pitot tube is fixed in a water pipe of diameter 14cm and difference of pressure by the gauge is 20cm of water column. Calculate the rate of flow of water.
View SolutionThe diameter of the throat of a venturimeter is 6 cm .when it is inserted in a horizontal pipe line of diameter 10 cm the pressure difference between the pipe and the thraot equal 8 cm of water . Calulate the rate of flow.
View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
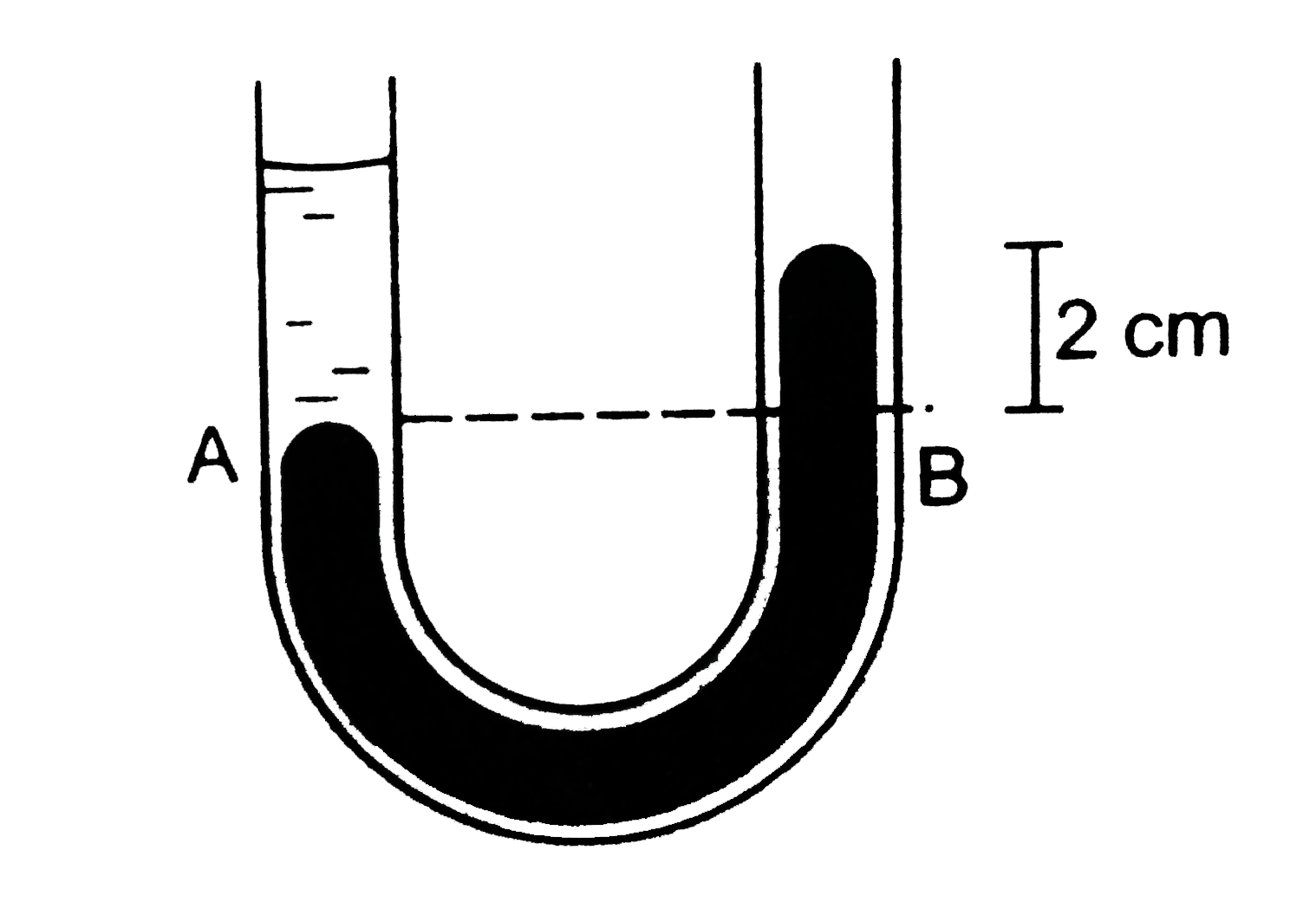 ,
,
View SolutionA pipe is running full of water. At a certain point A it tapers from 60cm diameter to 2.0cm diameter at B. The pressure difference between A and B is 100cm of water column. Find the rate of flow of water through the pipe.
View SolutionWhat is the power requird to raise 300 liters of water per minute through a height of 6 m using a pipe of diameter 2.5 cm ? g=10m/s2.
View SolutionThe diameters of open and narrow ends of a pipe connected to a venturi-meter is 20 cm and 15 cm, respectively. If the difference of pressure at the ends is 25 cm of Hg, then calculate the volume of water flowing through the pipe per second.
View Solution
