A water container has water upto a height of 20 cm, volume 2 litres. Top of container has area 60 cm2 and bottom has area of 20 cm2. The downward force exerted by water at the bottom will be.
200 N
100 N
222 N
122 N
The correct Answer is:C
To find the downward force exerted by water at the bottom of the container, we can follow these steps:
Step 1: Convert the height of water to meters
The height of water in the container is given as 20 cm. We need to convert this to meters for our calculations.
h=20cm=0.20m
Step 2: Calculate the pressure at the bottom of the container
The pressure at a certain depth in a fluid is given by the formula:
P=P0+ρgh
Where:
- P0 is the atmospheric pressure (approximately 1.01×105Pa),
- ρ is the density of water (1000kg/m3),
- g is the acceleration due to gravity (10m/s2),
- h is the height of the water column (in meters).
Substituting the values:
P=1.01×105Pa+(1000kg/m3)(10m/s2)(0.20m)
Calculating the second term:
P=1.01×105Pa+2000Pa
P=1.01×105Pa+2×103Pa=1.03×105Pa
Step 3: Calculate the area of the bottom of the container
The area of the bottom of the container is given as 20 cm². We need to convert this to square meters:
A=20cm2=20×10−4m2=0.002m2
Step 4: Calculate the force exerted at the bottom of the container
The force exerted by the water at the bottom can be calculated using the formula:
F=P×A
Substituting the values we have:
F=(1.03×105Pa)×(0.002m2)
Calculating the force:
F=1.03×105×0.002=206N
Final Answer
The downward force exerted by the water at the bottom of the container is 206 N.
---
The height of water in the container is given as 20 cm. We need to convert this to meters for our calculations.
The pressure at a certain depth in a fluid is given by the formula:
- P0 is the atmospheric pressure (approximately 1.01×105Pa),
- ρ is the density of water (1000kg/m3),
- g is the acceleration due to gravity (10m/s2),
- h is the height of the water column (in meters).
The area of the bottom of the container is given as 20 cm². We need to convert this to square meters:
The force exerted by the water at the bottom can be calculated using the formula:
The downward force exerted by the water at the bottom of the container is 206 N.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Competition File (B. MCQ (AIPMT/NEET & Other State Boards For Medical Entrance))
Explore 6 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Competition File (JEE (Main) & Other State Boards For Engineering Entrance)
Explore 23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Revision Exercise (Numerical Problems)
Explore 28 Videos
- MATHEMATICAL TOOLSBook:MODERN PUBLICATIONChapter:MATHEMATICAL TOOLSExercise:PRACTICE PROBLEMS (10)
Explore 12 Videos
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:Chapter Practice Test
Explore 15 Videos
Similar Questions
A curved glass vessel full of water upto a height of 10 cm has a bottom of area 10cm2, top of area 30cm2 and volume 1 L.
(i) Find the force exerted by the water on the bottom.
(ii) Find the resultant force exerted by the sides of the glass on the water.
(iii) If the glass vessel is covered by a jar and the air inside the jar is completely pumped out, what will be the answers to parts (a) and (b)
(iv) If a glass vessel of different shape is used provided the height, the bottom area and the volume are unchanged, will the answers to parts (a) and (b) change.
(Take, g=10ms−2 , density of water =103kgm−2 and atmospheric pressure =1.01×105Nm−2)
View SolutionA glass full of water upto a height of 10 cm has a bottom of are 10cm2, top of area 30cm2 and volume 1 litre.
(a) Find the force exerted by the water on the bottom.
(b) Find the resultant force exerted by the sides of the glass on the water.
(c ) If the glass is convered by a jar and the air inside the jar is completely pumped out, what will be the answer to parts (a) and (b).
(d) If a glass of different shape is used, provided the height, the bottom area, the top area and the volume are unchanged, will the answer to parts (a) and (b) change.
Take g=10m/s3, density of water=103kg/m3 and atmospheric pressure =1.01×105N/m2.
View Solution
Knowledge Check
A glass of water upto a height of 10 cm has a bottom of area 10cm2 , top of area 30cm2 and volume 1 litre. The downward force exerted by water on the bottom is…(Taking g=10m/s2 ,density of water =103kg/m3 , atmosphereic pressure =1.01×105N/m2)
A100 NB102 NC110 ND120 NIn a container, filled with water upto a height h, a hole is made in the bottom. The velocity of water flowing out of the hole is
Aproportional to hBproportional to h1/2Cproportional to h2Dindependent of hA cylinder containing water up to a height of 25cm has a hole of cross-section 14cm2 in its bottom. It is counterpoised in a balance. What is the intial change in the balancing weight when water begin to flow up?
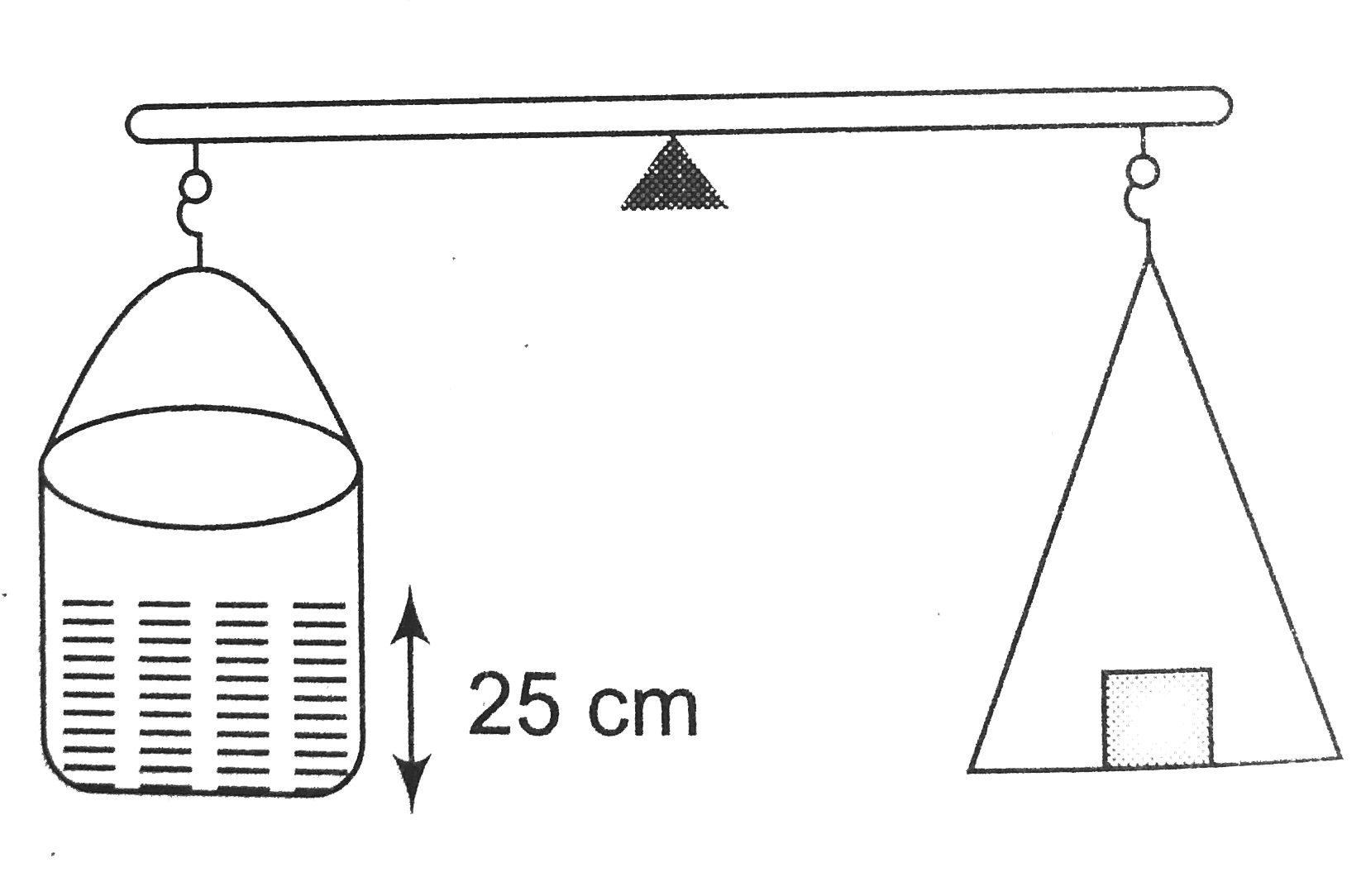 Aincreases of 12.5gwtBincrease of 6.25gwtCDecrease of 12.5gwtDDecrease of 6.25gwt
Aincreases of 12.5gwtBincrease of 6.25gwtCDecrease of 12.5gwtDDecrease of 6.25gwt
A container of filled with water to a height of 10 m.
The pressure exerted by the water at the bottom of the container is _________ .
View SolutionA vessel full of water has a bottom of area 20cm2, top of area 20cm2, height 20 cm and volume half a litre as shown in figure.
(a) find the force exerted by the water on the bottom.

(b) considering the equilibrium of the water, find the resultant force exerted by the sides of the glass vessel on the water. atmospheric pressure =1.0×105N/m2. density of water =1000kg/m3 and g=10m/s2
View SolutionWater is filled in a flask upto a height of 20cm. The bottom of the flask is circular with radius 10cm. If the atmospheric pressure is 1.013×105 Pa, find the force exerted by the water on the bottom . Take g=10ms−2 and density of water =1000kgm−3.
View SolutionWater is filled in a flask up top a heightof 20 cm. The bottom of the flask is circular with radius 10 cm.If the atmospheric pressure is 1.01×105 Pa, find the force exerted by the water on the bottom. Take g=10ms−2 and density of water =1000 kgm^-3.
View SolutionA container contains water up to a height of 20 cm and there is a point source at the centre of the bottom of the container. A rubber ring of radius r floats centrally on the water. The ceiling of the room is 2.0 m above the water surface. (a) Find the radius of the shadow of the ring formed on the ceiling if r = 15 cm. (b) Find the maximum value of r for which the shadow of the ring is formed on the ceiling. Refractive index of water =4/3.
View Solution