Calculate the force required to incrase the length of wire of cross-sectional area 10−6m2 by 50% if the Young's modulus of the material of the wire is 90×109Pa.
The correct Answer is:45000 N
To solve the problem of calculating the force required to increase the length of a wire by 50%, we can use the formula related to Young's modulus. Here’s a step-by-step solution:
Step 1: Understand the given data
- Cross-sectional area (A) = 10−6m2
- Young's modulus (Y) = 90×109Pa
- Change in length (ΔL) = 50% of original length (L)
Step 2: Express the change in length
Since the change in length is 50%, we can express it as:
ΔL=0.5L
Thus, the ratio ΔLL=0.5.
Step 3: Use the formula for Young's modulus
Young's modulus (Y) is defined as:
Y=F/AΔL/L
Where:
- F = Force applied
- A = Cross-sectional area
- ΔL/L = Change in length per unit original length
Rearranging the formula to solve for force (F):
F=Y⋅A⋅ΔLL
Step 4: Substitute the values into the formula
Now we can substitute the known values into the formula:
F=(90×109Pa)⋅(10−6m2)⋅(0.5)
Step 5: Calculate the force
Calculating the force:
F=90×109⋅10−6⋅0.5
F=90×0.5×103
F=45×103
F=45000N
Final Answer
The force required to increase the length of the wire by 50% is 45000 N.
---
- Cross-sectional area (A) = 10−6m2
- Young's modulus (Y) = 90×109Pa
- Change in length (ΔL) = 50% of original length (L)
Since the change in length is 50%, we can express it as:
ΔL=0.5L
Thus, the ratio ΔLL=0.5.
Young's modulus (Y) is defined as:
Y=F/AΔL/L
Where:
- F = Force applied
- A = Cross-sectional area
- ΔL/L = Change in length per unit original length
F=Y⋅A⋅ΔLL
Now we can substitute the known values into the formula:
F=(90×109Pa)⋅(10−6m2)⋅(0.5)
Calculating the force:
F=90×109⋅10−6⋅0.5
F=90×0.5×103
F=45×103
F=45000N
The force required to increase the length of the wire by 50% is 45000 N.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY) FROM BULK MODULUS
8 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY) FROM RIGIDITY MODULUS AND POISSON.S RATIO
7 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 1 (ELASTICITY)VERY SHORT ANSWER QUESTIONS
8 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- SAMPLE QUESTION PAPER - 01 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D
12 Videos
Similar Questions
A force of one newton doubles the length of a cord having cross-sectional area 1mrh2. The Young's modulus of the material of the cord is
View SolutionThe adjacent graph shows the extra extension (Δx) of a wire of length 1m suspended from the top of a roof at one end with an extera load Δw connected to the other end If the cross sectional area of the wire is 10−5m2 calculate the Young's modulus of the meterial of the wire
(A) 2×1011N/m2 (B) 2×10−11N/m2 (c) 3×10913)N/m3 (D) 2×1016N/m2
 .
.
View Solution
Knowledge Check
The adjacent graph shows the extension Δl of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 106m2 calculate the young's modulus of the material of the wire .
 A2×1011N/m2B2×10−11N/m2C3×10−12N/m2D2x10−13N/m2
A2×1011N/m2B2×10−11N/m2C3×10−12N/m2D2x10−13N/m2
The adjacent graph shows the extension Δl of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 106m2 calculate the young's modulus of the material of the wire .

View SolutionFind the percentage increase in length of a wire subjected to a stress of 1 gm. Wt /mm2 . Young's modulus of the material of the wire = 100 Gpa.
View SolutionA uniform wire of length 6m and a cross-sectional area 1.2 cm2 is stretched by a force of 600N . If the Young's modulus of the material of the wire 20×1010Nm−2 , calculate (i) stress (ii) strain and (iii) increase in length of the wire.
View SolutionThe adjacent graph shows the estension (Δl) of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is 10−6m2, calculate the Young's modulus of the material of the wire.
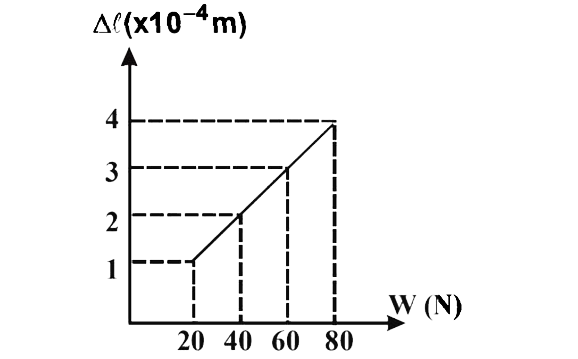
View Solution_S01_065_Q01.png)
The graph shows the extension of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1mm2, then the young's modulus of the material of the wire is
(a). 2×1011Nm−2
(b). 2×1010Nm−2
(c). 12×1011Nm−2
(d). none of these
View SolutionFind the work done in stretching a wire Im long and area of cross section 0.03 cm under a load of 100 N if Young.s modulus of the material of the wire is 2×1011N/m2
View SolutionA force F doubles the length of wire of cross-section a The Young modulus of wire is
View Solution
