A force of one newton doubles the length of a cord having cross-sectional area 1mrh2. The Young's modulus of the material of the cord is
1Nm−2
5×105Nm−2
106Nm−2
2×106Nm−2
The correct Answer is:C
To find the Young's modulus of the material of the cord, we can follow these steps:
Step 1: Identify the given values
- Force (F) = 1 N
- Change in length (ΔL) = L (since the length doubles, ΔL = L)
- Cross-sectional area (A) = 1 mm² = 1 × 10⁻⁶ m²
Step 2: Understand the formula for Young's modulus
Young's modulus (Y) is defined as the ratio of stress to strain:
Y=StressStrain
Where:
- Stress = FA
- Strain = ΔLL
Step 3: Calculate stress
Using the formula for stress:
Stress=FA=1 N1×10−6 m2=1×106 N/m2
Step 4: Calculate strain
Since the length doubles, the change in length (ΔL) is equal to the original length (L):
Strain=ΔLL=LL=1
Step 5: Substitute values into the Young's modulus formula
Now, substituting the values of stress and strain into the Young's modulus formula:
Y=StressStrain=1×106 N/m21=1×106 N/m2
Step 6: Conclusion
Thus, the Young's modulus of the material of the cord is:
Y=106 N/m2
Final Answer:
The Young's modulus of the material of the cord is 106 N/m2.
---
- Force (F) = 1 N
- Change in length (ΔL) = L (since the length doubles, ΔL = L)
- Cross-sectional area (A) = 1 mm² = 1 × 10⁻⁶ m²
Young's modulus (Y) is defined as the ratio of stress to strain:
Y=StressStrain
- Stress = FA
- Strain = ΔLL
Using the formula for stress:
Stress=FA=1 N1×10−6 m2=1×106 N/m2
Since the length doubles, the change in length (ΔL) is equal to the original length (L):
Strain=ΔLL=LL=1
Now, substituting the values of stress and strain into the Young's modulus formula:
Y=StressStrain=1×106 N/m21=1×106 N/m2
Thus, the Young's modulus of the material of the cord is:
Y=106 N/m2
The Young's modulus of the material of the cord is 106 N/m2.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment (SECTION - C)
2 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment (SECTION - D)
3 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment (SECTION - A)
31 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
- Mock test 03BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - Mock test 03EXERCISE - EXAMPLE
44 Videos
Similar Questions
Calculate the force required to incrase the length of wire of cross-sectional area 10−6m2 by 50% if the Young's modulus of the material of the wire is 90×109Pa.
View SolutionA uniform wire of length 6m and a cross-sectional area 1.2 cm2 is stretched by a force of 600N . If the Young's modulus of the material of the wire 20×1010Nm−2 , calculate (i) stress (ii) strain and (iii) increase in length of the wire.
View Solution
Knowledge Check
The adjacent graph shows the extension Δl of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 106m2 calculate the young's modulus of the material of the wire .
 A2×1011N/m2B2×10−11N/m2C3×10−12N/m2D2x10−13N/m2
A2×1011N/m2B2×10−11N/m2C3×10−12N/m2D2x10−13N/m2
The adjacent graph shows the estension (Δl) of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is 10−6m2, calculate the Young's modulus of the material of the wire.
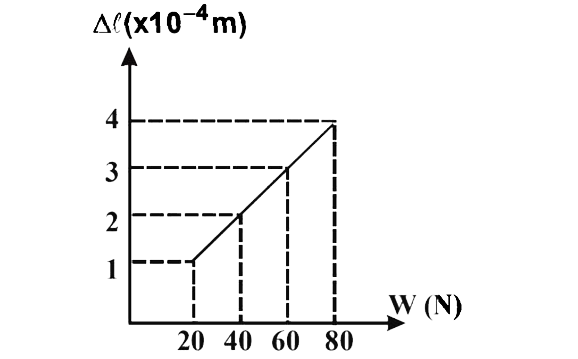
View SolutionThe adjacent graph shows the extension Δl of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 106m2 calculate the young's modulus of the material of the wire .

View SolutionA force F doubles the length of wire of cross-section a The Young modulus of wire is
View SolutionThe stress along the length of a rod with rectangular cross section) is 1% of the Young's modulus of its material. What is the approximate percentage of change of its volume? (Poisson's ratio of the material of the rod is 0.3)
View SolutionAn object of mass m is suspended at the end of a massless wire of length L and area of cross -section A. Young modulus of the material of the wire is Y. If the mass is pulled down slightly its frequency of oscillation along the vertical direction is :
View SolutionThe length of a rod is 20cm and area of cross-section 2cm2. The Young's modulus of the material of wire is 1.4×1011N/m2. If the rod is compressed by 5kg−wt along its length, then increase in the energy of the rod in joules will be
View SolutionA uniform bar of length 2 m and cross-sectional area 50cm2 is subjected to a tensile load 100 N. If Young's modulus of material of bar is 2×107N/m2 and poisson's ratio is 0.4, then determine the volumetric strain.
View Solution
