Calculate the length of mercury column in a barometer tube which is inclined at an angle of 45∘ with horizontal direction if the atmospheric pressure is 75 cm of mercury.
To calculate the length of the mercury column in a barometer tube inclined at an angle of 45 degrees with the horizontal, given that the atmospheric pressure is 75 cm of mercury, we can follow these steps:
1. Understand the Problem: We know that the atmospheric pressure can support a column of mercury. When the barometer tube is inclined, we need to consider only the vertical component of the mercury column.
2. Identify the Vertical Component: When the barometer tube is inclined at an angle of 45 degrees, the vertical height (h) of the mercury column can be expressed in terms of the length of the mercury column (L) as:
h=Lsin(45∘)
3. Set Up the Equation: The atmospheric pressure (P) is given as 75 cm of mercury. This pressure is equal to the vertical height of the mercury column:
P=h=Lsin(45∘)
Therefore, we can write:
75cmHg=Lsin(45∘)
4. Substitute the Value of Sine: We know that:
sin(45∘)=1√2
Substituting this into the equation gives:
75=L⋅1√2
5. Solve for L: Rearranging the equation to find L:
L=75⋅√2
6. Calculate the Numerical Value: Now, calculating the value:
L≈75⋅1.414≈106.06cm
Final Answer:
The length of the mercury column in the inclined barometer tube is approximately 106.06 cm.
---
h=Lsin(45∘)
P=h=Lsin(45∘)
Therefore, we can write:
75cmHg=Lsin(45∘)
sin(45∘)=1√2
Substituting this into the equation gives:
75=L⋅1√2
L=75⋅√2
L≈75⋅1.414≈106.06cm
The length of the mercury column in the inclined barometer tube is approximately 106.06 cm.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Practice Problems
52 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Conceptual Questions
29 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
A barometer tube is inclined at an angle of 30∘ with horizontal direction. Calculate length of mercury column in tube if atmospheric pressure is 76 cm of mercury.
View SolutionWhat will be the length of mercury column in a barometer tube when the atmosperic pressure is 75cm of mercury and the tube is inclined at an angle of 60∘ with the horizontal direction?
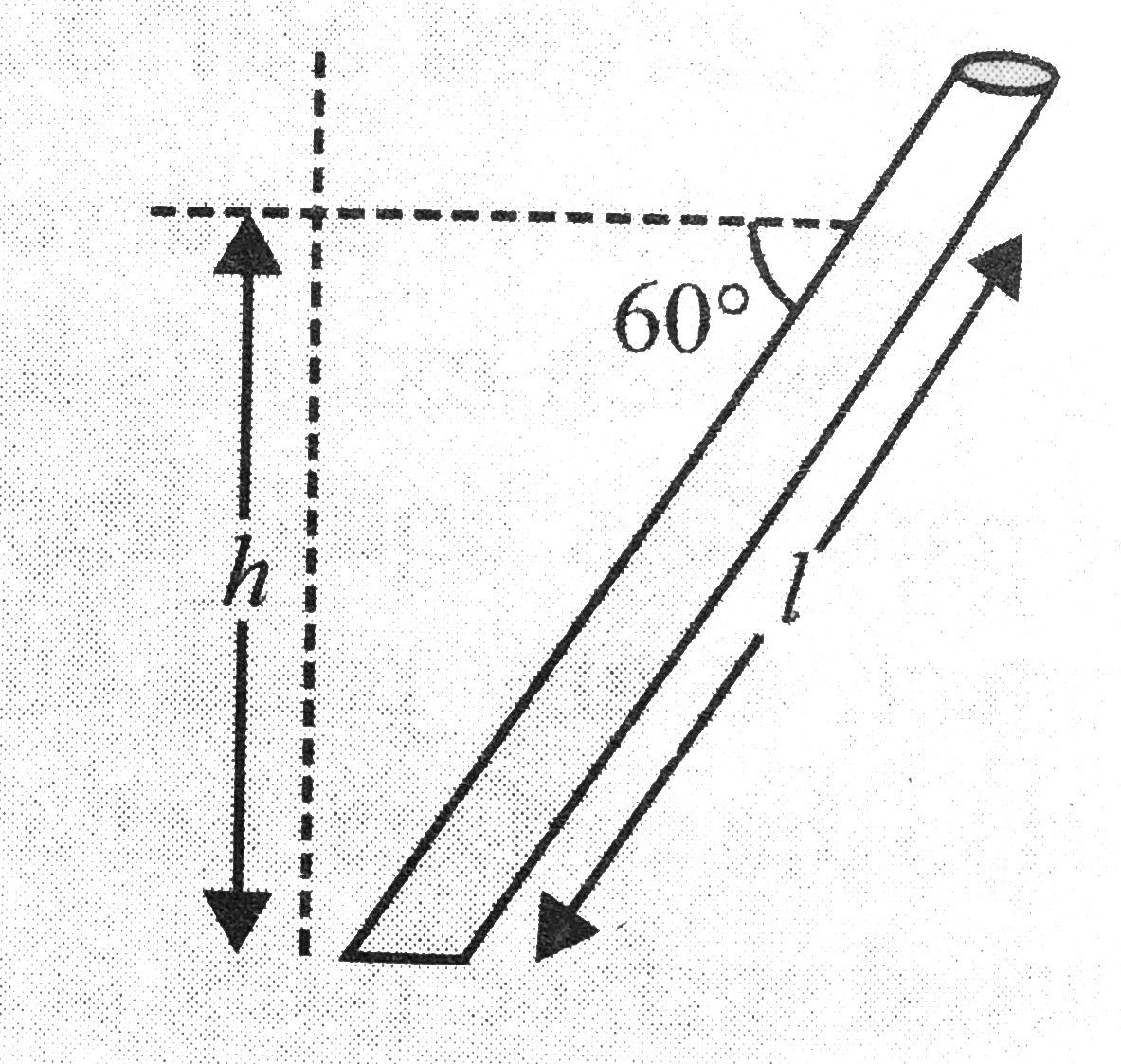
View Solution
Knowledge Check
A manometer is connected to gas container. Then the mercury level rises by 2 cm in the arm of the manometer which is not connected to the container.
If the atmospheric pressure is 76 cm of mercury, then the pressure of the gas is ________ cm of mercury.A80B76C72D78What will be the length of mercury column in a barometer tube when the atmospheric pressure is x cm of mercury and the tube is inclined at an angle ϕ with the vertical direction ?
AxsinϕBxcosϕCxtanϕDx
What will be the length of mercury column in a barometer tube, when the atmospheric pressure is 76 cm of mercury and the tube is inclined at an angle of 30∘ with the horizontal direction ?
View SolutionCalculate the atmospheric pressure , if the height of mercury column in a barometer is 760 mm
View SolutionIf the length of the mercury column in a mercury barometer is 76 cm, what is the equivalent height of the water column ?
View SolutionA vertical cylinder of height 100cm contains air at a constant temperature. The top is closed by a friction less light piston. The atmospheric pressure is equal to 75 cm of mercury. Mercury is slowly poured over the piston. Find the maximum height of the mercury column that can be put on the piston.
View SolutionA barometer tube reads 75 cm of Hg. If tube is : gradually inclined at an angle of 30∘ with horizontal, keeping the open end in the mercury container, then find the length of mercury column in the barometer ■ tube
View SolutionA berometer correctlu reads the atmospheric pressure as 76cm of mercury. Water droplets are slowly introduced into the barometer tube by a dropper. The height of the mercury column first decreases and then become constant. If the saturation vapour pressure at the atmospheric tgemperature is 0.80cm of mercury, find the height if the mercury column when it reaches its minimum value.
View Solution
