Question

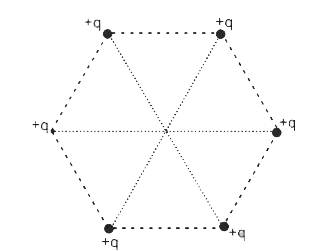
Calculate the magnitude of electric field at the centre of a regular hexagon of side 2.5 cm, if each charge placed at its vertex has the same magnitude of +0.01 $\mu$C.

Explanation

To solve the problem of calculating the magnitude of the electric field at the center of a regular hexagon with charges at its vertices, we can follow these steps:

1. Understanding the Configuration:
- We have a regular hexagon with each side measuring 2.5 cm.
- There are six identical charges of +0.01 µC placed at each vertex of the hexagon.

2. Finding the Distance from the Center to a Vertex:
- The distance from the center of the hexagon to any vertex can be calculated using the formula for the circumradius (R) of a regular hexagon:
\( R = \frac{a}{\sqrt{3}} \quad \text{(where } a \text{ is the side length)} \)
- Here, \( a = 2.5 \, \text{cm} = 0.025 \, \text{m} \).
- Therefore,
\( R = \frac{0.025}{\sqrt{3}} \approx 0.01443 \, \text{m} \)

3. Calculating the Electric Field due to One Charge:
- The electric field (E) due to a point charge (Q) at a distance (r) is given by:
\( E = \frac{k \cdot |Q|}{r^2} \)
- Where \( k \) (Coulomb's constant) is approximately \( 8.99 \times 10^9 \, \text{N m}^2/\text{C}^2 \) and \( Q = 0.01 \, \mu\text{C} = 0.01 \times 10^{-6} \, \text{C} \).
- Substituting the values:
\( E = \frac{8.99 \times 10^9 \cdot 0.01 \times 10^{-6}}{(0.01443)^2} \)

4. Calculating the Total Electric Field:
- Since the hexagon is symmetrical, the electric fields due to the charges at opposite vertices will cancel each other out in the horizontal direction.
- The vertical components of the electric fields from the charges will add up.
- Each charge contributes equally to the vertical component of the electric field at the center. The total electric field at the center can be calculated as:
\( E_{\text{total}} = 6 \cdot E \cdot \sin(60^\circ) = 6 \cdot E \cdot \frac{\sqrt{3}}{2} \)

5. Final Calculation:
- Substitute the value of E from step 3 into the equation from step 4 to find the total electric field at the center of the hexagon.