A positive charge Q is uniformly distributed along the length L of a rod. It is bent in the shape of a square. Calculate electric field intensity at the centre of the square.
To calculate the electric field intensity at the center of a square formed by bending a uniformly charged rod, we can follow these steps:
Step 1: Understand the Charge Distribution
The total positive charge Q is uniformly distributed along the length L of the rod. When the rod is bent into a square shape, each side of the square will have a charge of Q4.
Step 2: Identify the Geometry
The square has four equal sides. Let’s denote the length of each side of the square as a. Since the total length L of the rod is equal to the perimeter of the square, we have:
L=4a⇒a=L4
Step 3: Calculate Electric Field Due to One Side
The electric field dE at the center of the square due to a small segment dx of one side can be expressed using Coulomb's law. The electric field due to a small charge dq is given by:
dE=14πϵ0dqr2
where r is the distance from the charge to the center of the square.
For a uniformly charged rod, we can express dq as:
dq=Q4adx
Step 4: Determine the Distance
The distance r from any point on the side of the square to the center is a√2 because the center is at equal distance from all corners of the square.
Step 5: Calculate the Total Electric Field
The electric field due to one side of the square will have both x and y components. However, due to symmetry, the horizontal components from opposite sides will cancel each other out, and only the vertical components will add up.
Thus, the total electric field E at the center due to all four sides can be calculated as:
Enet=4⋅Ey
where Ey is the vertical component of the electric field due to one side.
Step 6: Consider Symmetry
Since the square is symmetric and the charge distribution is uniform, the electric field contributions from opposite sides will cancel out in the horizontal direction. Therefore, the net electric field at the center of the square is:
Enet=0
Conclusion
The electric field intensity at the center of the square formed by the uniformly charged rod is:
0
The total positive charge Q is uniformly distributed along the length L of the rod. When the rod is bent into a square shape, each side of the square will have a charge of Q4.
The square has four equal sides. Let’s denote the length of each side of the square as a. Since the total length L of the rod is equal to the perimeter of the square, we have:
L=4a⇒a=L4
The electric field dE at the center of the square due to a small segment dx of one side can be expressed using Coulomb's law. The electric field due to a small charge dq is given by:
dE=14πϵ0dqr2
where r is the distance from the charge to the center of the square.
dq=Q4adx
The distance r from any point on the side of the square to the center is a√2 because the center is at equal distance from all corners of the square.
The electric field due to one side of the square will have both x and y components. However, due to symmetry, the horizontal components from opposite sides will cancel each other out, and only the vertical components will add up.
Enet=4⋅Ey
where Ey is the vertical component of the electric field due to one side.
Since the square is symmetric and the charge distribution is uniform, the electric field contributions from opposite sides will cancel out in the horizontal direction. Therefore, the net electric field at the center of the square is:
Enet=0
The electric field intensity at the center of the square formed by the uniformly charged rod is:
0
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Conceptual Questions
51 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Tough & Tricky Problems
20 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
A positive charge Q is uniformly distributed across a rod of length L. The rod is then bent in the form of a semicircle. What will be the electric field intensity at the centre of curvature of the semicircle thus formed?
View SolutionPositive charge Q is uniformly distributed across a thin rod of length L. The rod is then bent in the form of a semicircle. What will be the electric potential at the centre of curvature of semicircle formed?
View Solution
Knowledge Check
A wire of length l and mass m is bent in the form of a semicircle. The gravitational field intensity at the centre of semicircle is
 AGmπl along x- axisBGmπl along y-axisC2pGml2 along y-axisD2πGml2 along x-axis
AGmπl along x- axisBGmπl along y-axisC2pGml2 along y-axisD2πGml2 along x-axisCharge q is uniformly distributed on a disc of radius r. If the disc is rotated with a frequency v, then magnetic field induction at the centre will be
Aμ0qvrBμ0qvrCμ0vqrDμ0qvrA thin glass rod is bent into a semicircle of radius r. A charge +Q is uniformly distributed along the lower half, as shown in fig. The electric field E at P, the center of the semicircle, is
 AQπ2ε0r2B2Qπ2ε0r2C4Qπ2ε0r2DQ4π2ε0r2
AQπ2ε0r2B2Qπ2ε0r2C4Qπ2ε0r2DQ4π2ε0r2
A rod of length L has a total charge Q distributed uniformly along its length. It is bent in the shape of a semicircle. Find the magnitude of the electric field at the centre of curvature of the semicircle.
View SolutionTwo point charges +Q each are placed at adjacent corners of a square. Other two point charges -Q each are placed at the remaining two corners of the same square . The side of the square is l. Find electric field intensity at the centre of the square.
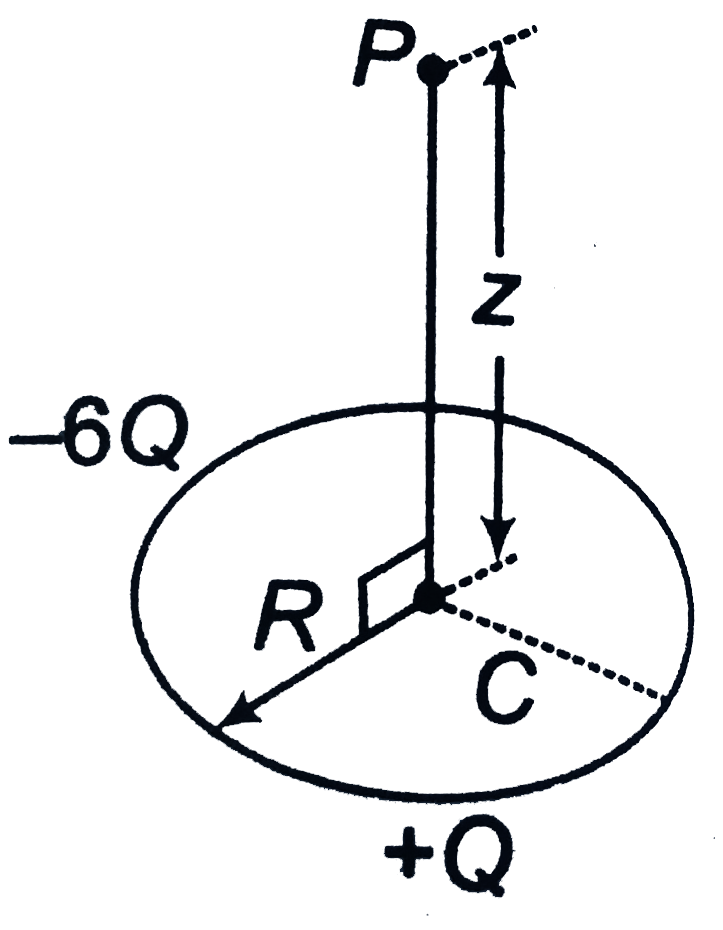
View SolutionA plastic rod has been formed into a circle of radius R. It has a positive charge +Q uniformly distributed along one-quarter of its circumference and a negative charge of −6Q uniformly distributed along the rest of the circumference (figure). With V = 0 at infinity, what is the electric potential −6Q
(a) at the centre C of the circle and
(b) at point P, which is on the central axis of the circle at distance z from the centre?
View SolutionThere is a hemispherical shell having charge Q uniformly distributed on its surface. Radius of the shell is R. Find electric potential and field at the centre (of the sphere).
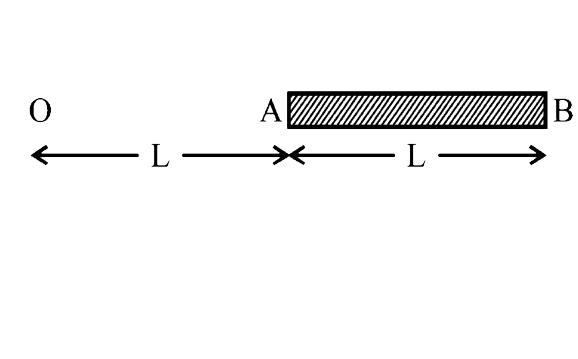
View SolutionA charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point O lying at distance L from the end A is
View Solution
