Calculate the maximum current in the circuit, if a capacitor of capacitance 1μF is charged to a potential of 2 V and is connceted in parallel to an inductor of inductance 10−3H.
√4000 mA
√2000 mA
√1000 mA
√5000 mA
(a) charge on capacitor q0=CV q0=2×10−6C Here, q=q0sinωt
For maximum current=I0=dqdt=ωq0
ω=1√LC=(109)1/2,I0=(109)1/2(2×10−6)
=√10×104×2×10−6=2√10×10−2A=√4000 mA
Topper's Solved these Questions
Similar Questions
Two parallel plate capacitors of capacitances 2 μF and 3 μF are connected in series. Calculate the maximum voltage, for the combination if capacitor of capacitance 3μF can withstand a voltage of 6 kV and capacitor of capacitance 2μF can withstand a voltage of 7 kV.
View SolutionThe voltage between the plates of a parallel plate capacitor of capacitance 1.0μFis changing at rate of 1.0V/s. Find displacement current
View Solution
Knowledge Check
A capasitor of capacitance 1(μ)F is charged to a potential of 1 V, it is connected in parallel to an inductor of inductance 10−3H. The maximum current that will flow in the circuit has the value
A(A) √1000mAB(B) 1mAC(C) 1(μ)AD(D) 1000mAA capacitor of capacitance 50μF is charged to 10 V. Its electrostatic potential energy is
A2.5×10−3JB2.5×10−4JC5×10−2JD1.2×10−5JA capacitor having capacitance 2 μF is charged to a potential difference of 50 V. it is then diconnected from battery and connected to an inductor of inductance 5 mH. Peak current that flows through the inductor is
A1AB2AC3AD4A
Two capacitors of capacitance 10 μF and 20 μF are charged to potential 20 V and 10 V respectively. If they are connected to share charges, then loss of energy is
View SolutionA capacitor of capacitance 1μF is charged to a potential of 20 volt. The battery is then disconnected and a pure inductive coil of inductance 10 mH is connected across the capacitor so that L-C oscillation are set-up in the circuit. What is the maximum current in the circuit?
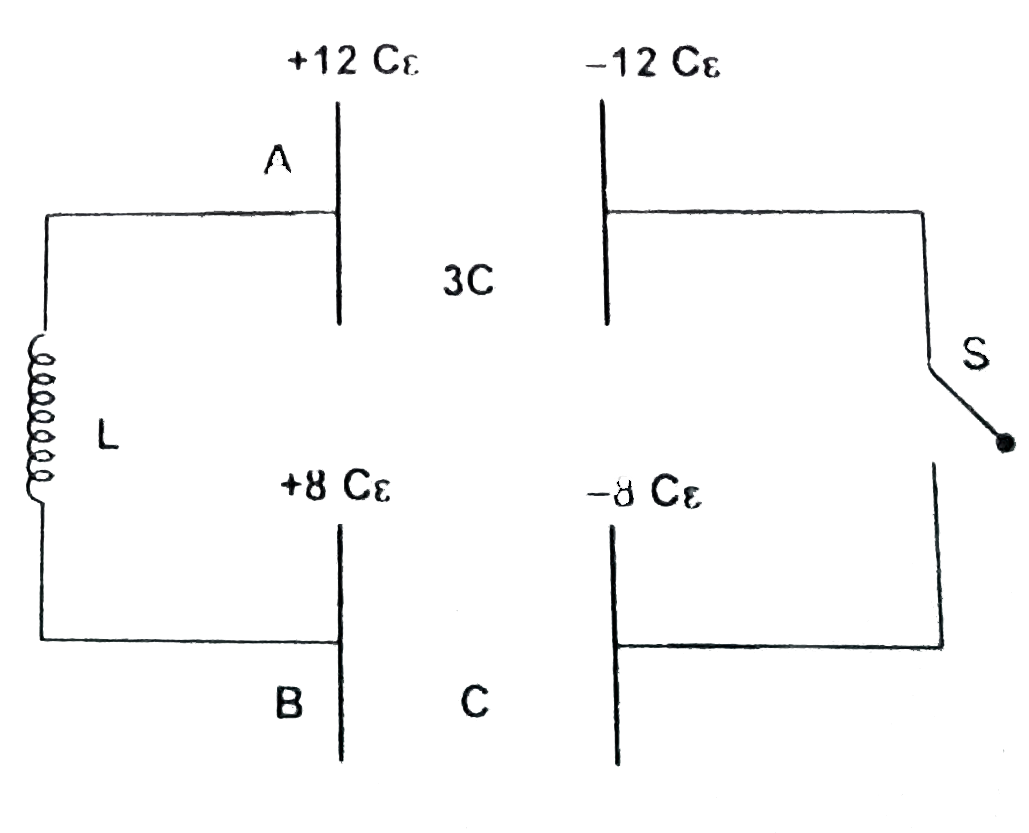
View SolutionIn the adjacent circuit, the capacitor 'A' of capacitance '3C' and the capacitor 'B' of capacitance 'C' are initially charged by potential drops 4ɛ and 8ɛ respectively and connected through and inductor of inductance 'L' with zero initial current as shown. The switch 'S' is closed at t=0. then the maximum current through the inductor is
View SolutionA capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
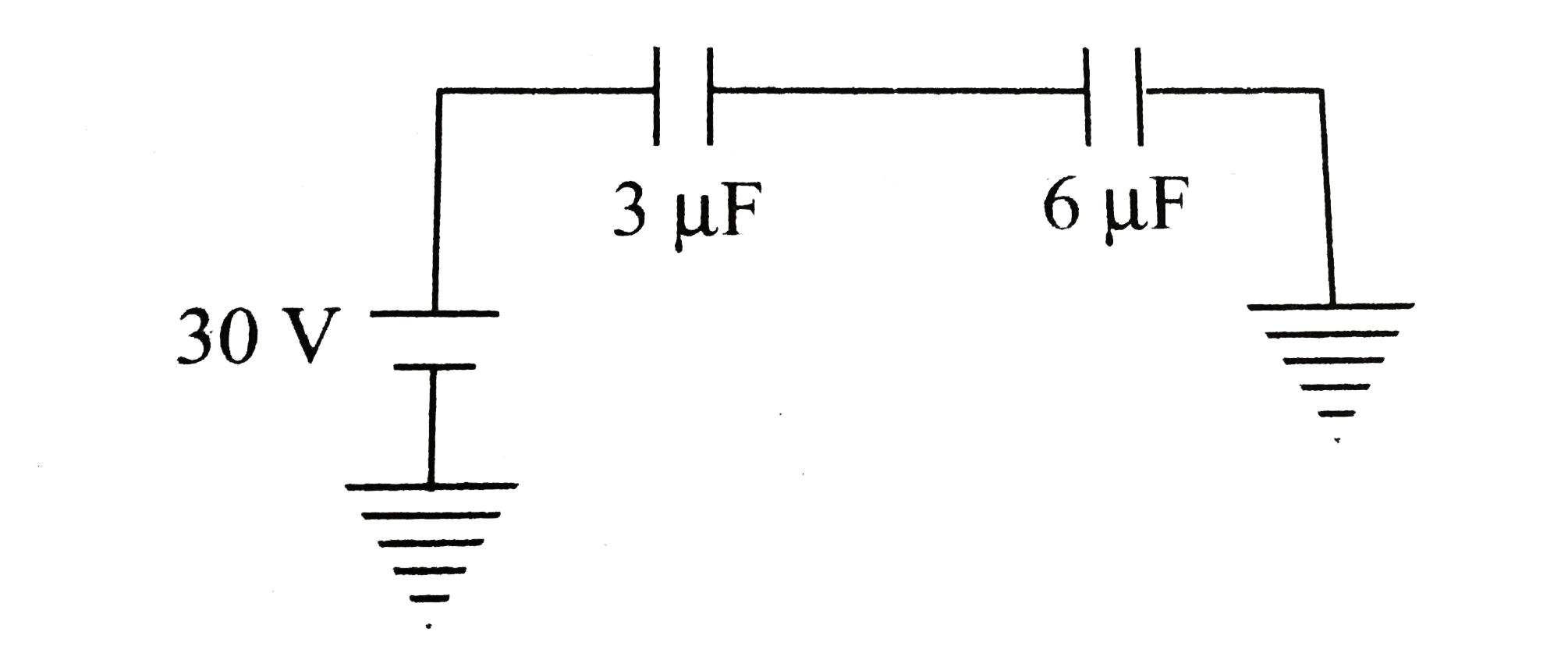
View SolutionIn the circuit shown in figure, the charge stored on a capacitor of capacitance 3μF is
View Solution
