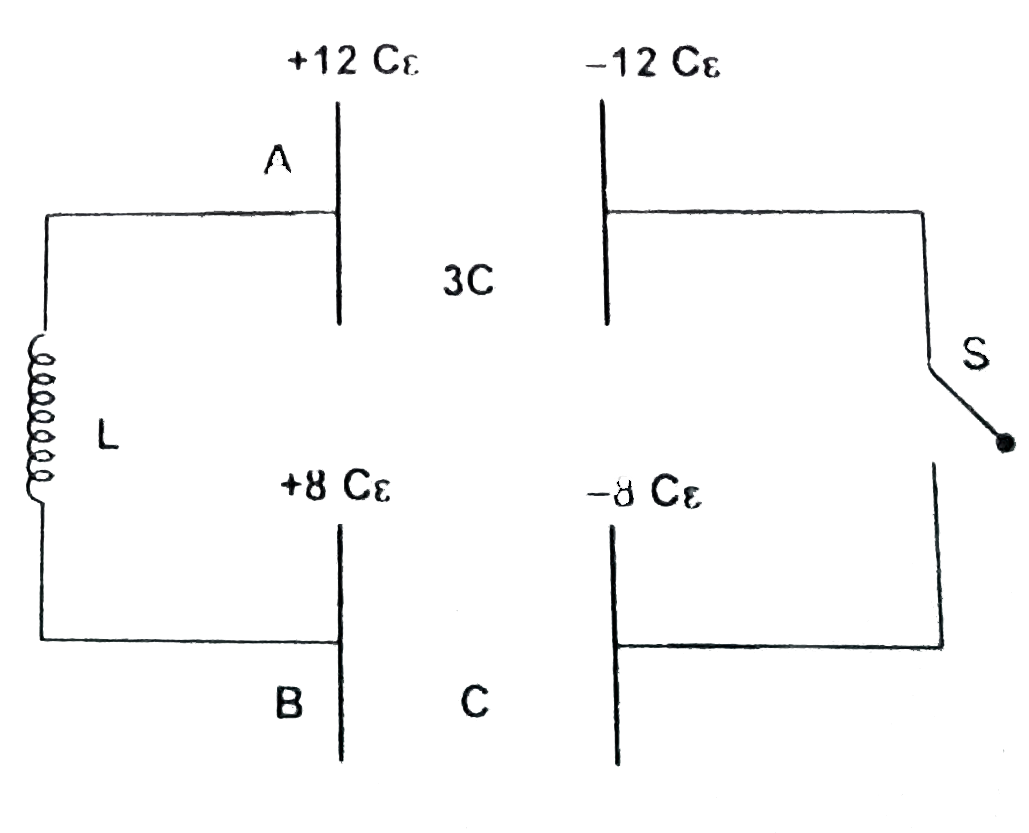
In the adjacent circuit, the capacitor 'A' of capacitance '3C' and the capacitor 'B' of capacitance 'C' are initially charged by potential drops 4ɛ and 8ɛ respectively and connected through and inductor of inductance 'L' with zero initial current as shown. The switch 'S' is closed at t=0. then the maximum current through the inductor is
ɛ√3CL
ɛ√6CL
ɛ√12CL
ɛ√15CL
The correct Answer is:C
When the cuurent through the inductor is maximum,
VL=Ldidt=0
Now, using energy conservation
12Li2max=(12×3C×16ε2+12C×64ε2)−12(3C+C)25ε2
12Li2max=56Cε2−50Cε2
12Li2max=6Cε2
∴imax=ε√12CL
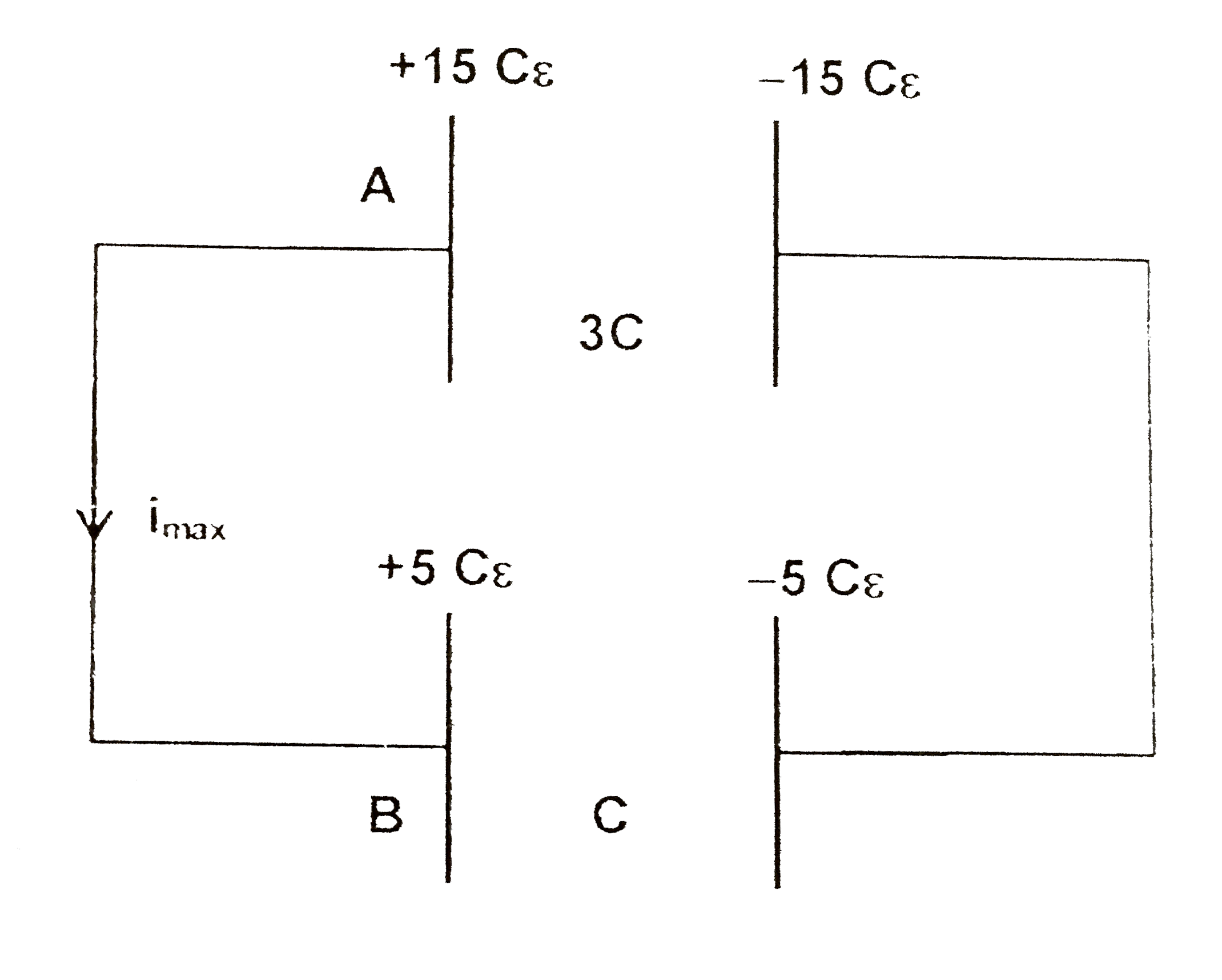
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)20videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)5videos
WORK, ENERGY AND POWER
Similar Questions
In the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.
 View Solution
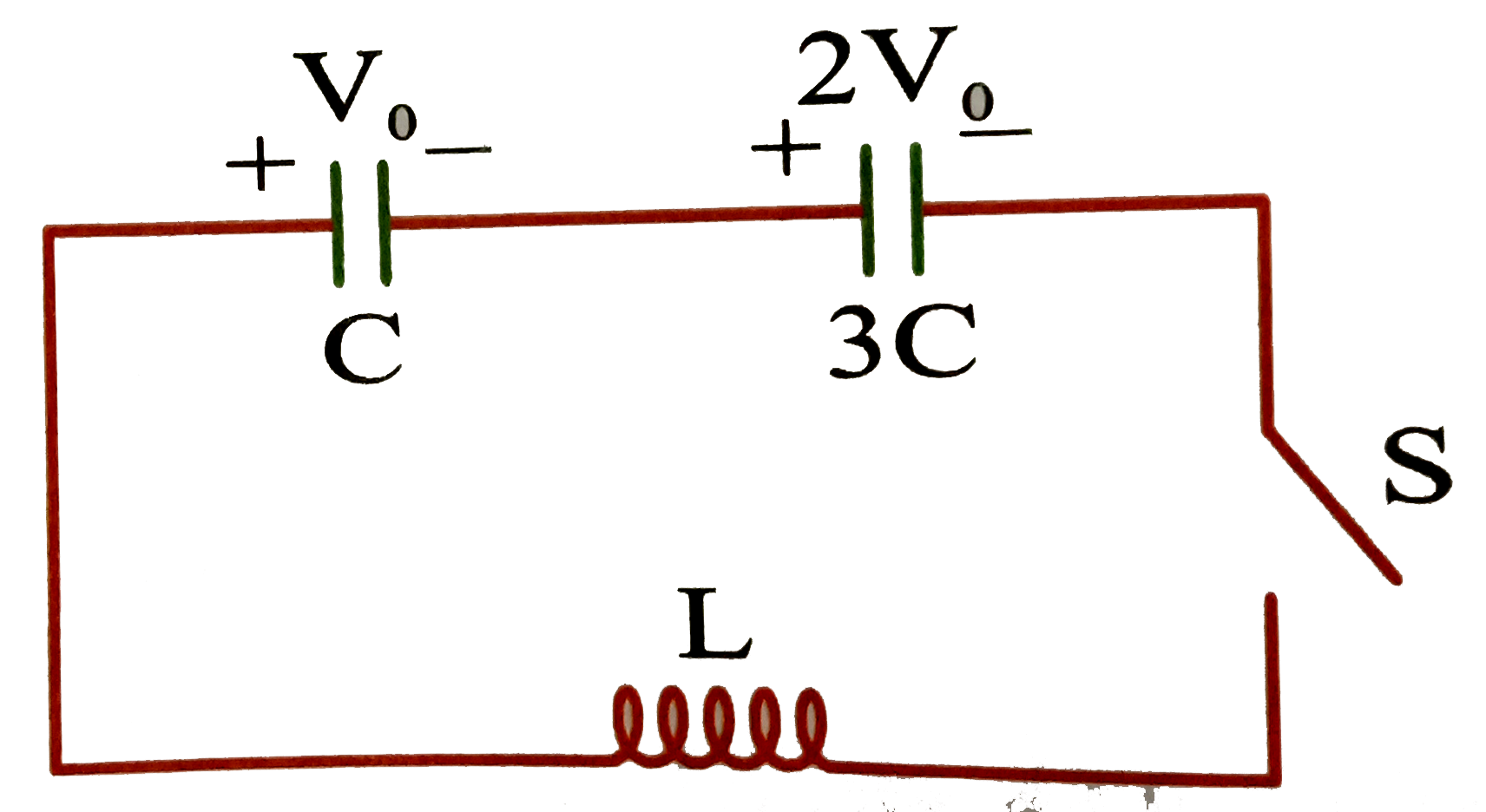
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance 3C when the current in the circuit is maximum isView Solution
Knowledge Check
- Question 1 - Select One
Two capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0 respectively, and connected to an inductor of inductance L as shown in figure. Initially the current in the inductor is zero. Now, the switch S is closed.

The maximum current in the indcutor is :A3V02√3CLBV0√3CLC2V0√3CLDV0√CL - Question 2 - Select One
Two capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
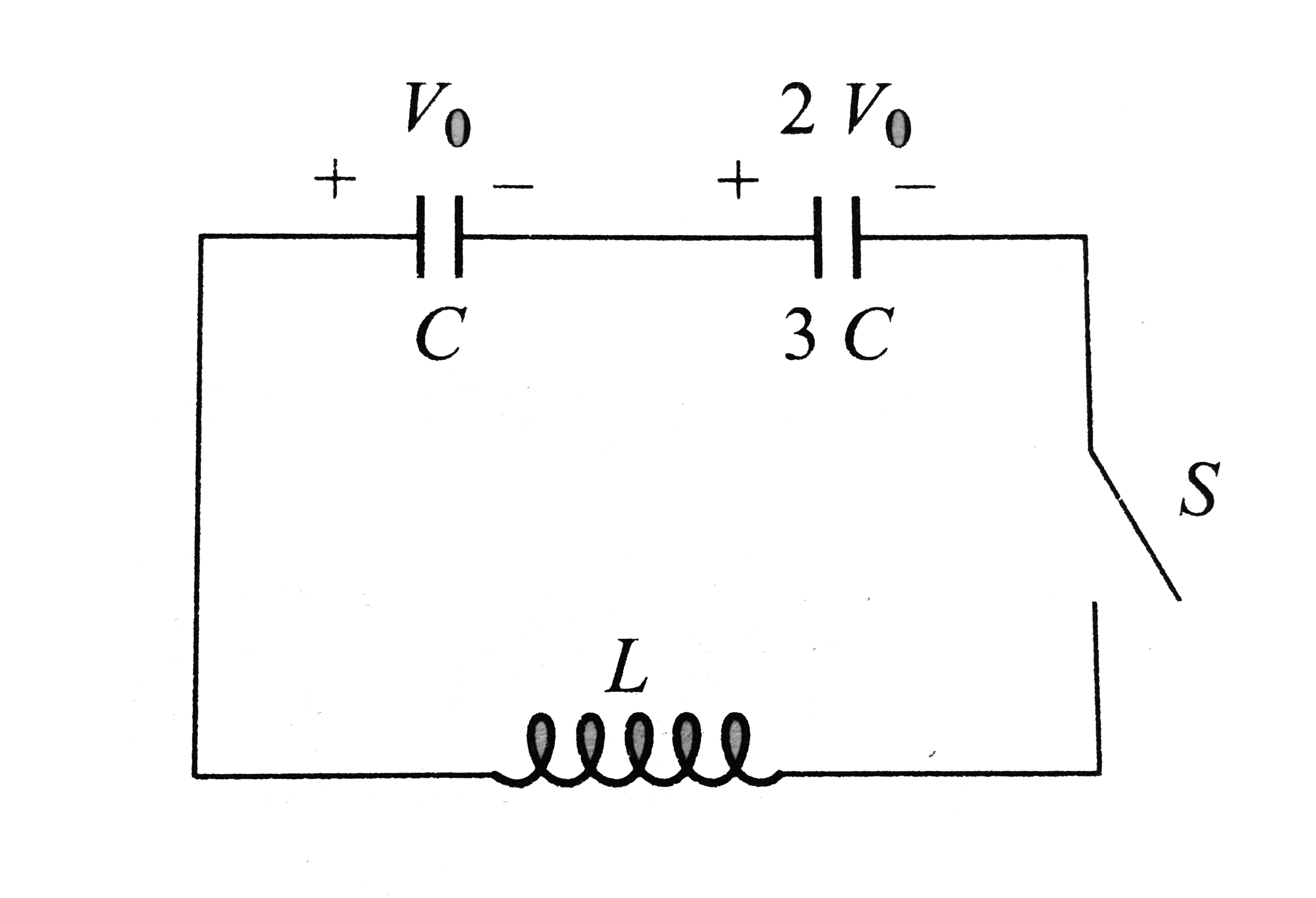
The maximum current in the inductor isA3V02√3CLBV0√3CLC2V0√3CLDV0√CL - Question 3 - Select One
Two capacitors 2C and 4C initially charged to potential difference of V0and3V0 with the potential as show are connected to an inductor of inductance L. Initial curren tin the inductor is zer. Now the swtich 'S' is closed. The maxmimum current in the circuit is
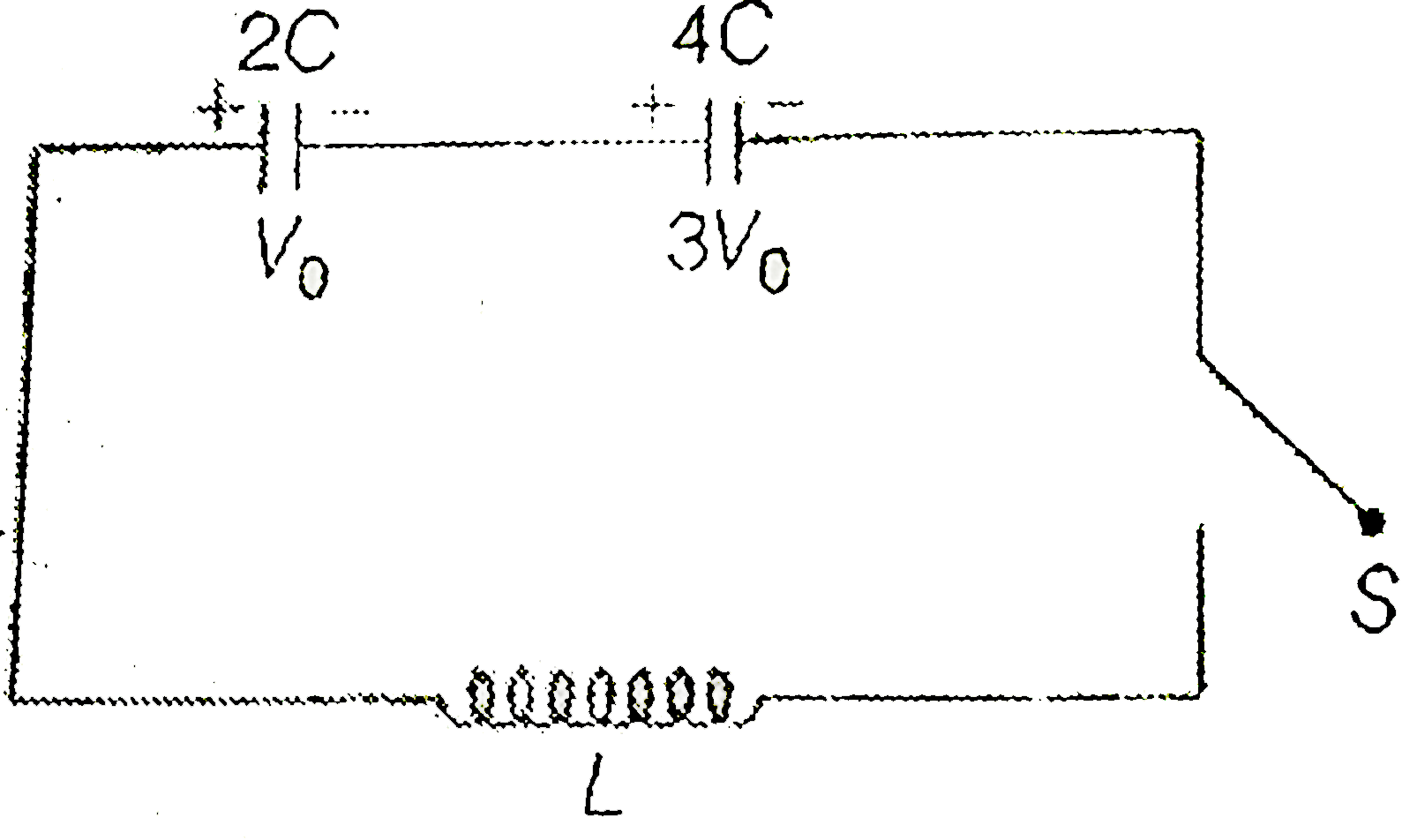 AV08√C3LB(8V0)√C3LCV04√C3LD4V0√C3L
AV08√C3LB(8V0)√C3LCV04√C3LD4V0√C3L
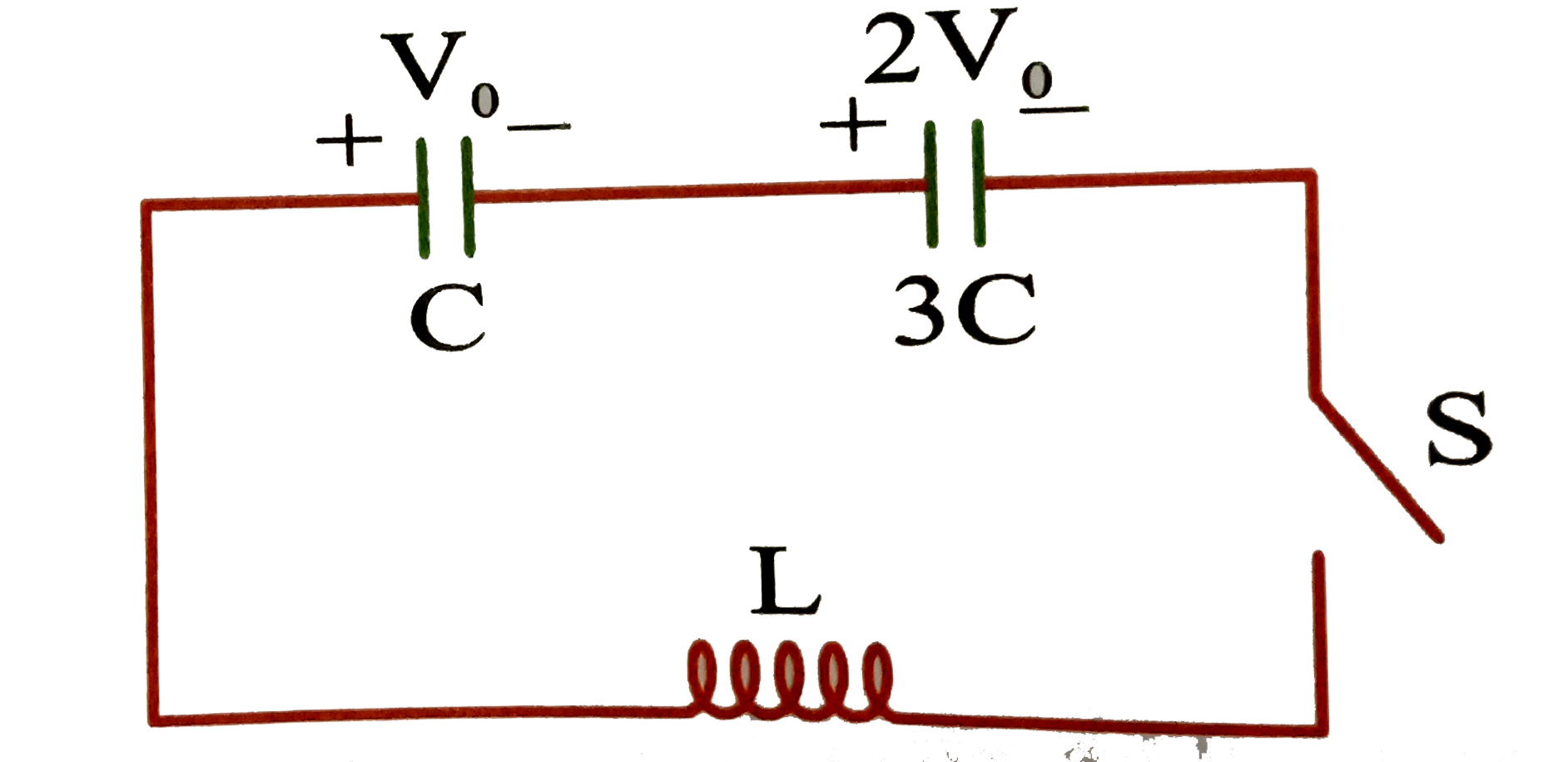
Two capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance C when the current in the circuit is maximum isView SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0 respectively, and connected to an inductor of inductance L as shown in figure. Initially the current in the inductor is zero. Now, the switch S is closed.
Potential difference across capacitor of capacitance 3C when the current in the cirucit is maximum is :View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0 respectively, and connected to an inductor of inductance L as shown in figure. Initially the current in the inductor is zero. Now, the switch S is closed.
Potential difference across capacitor of capacitance C when the current in the cirucit is maximum isView Solutionthere in no current part of this circuit for time t<o. Switch S is closed at t=0.

The current through the inductor after a long time will beView Solutionthere in no current part of this circuit for time t<o. Switch S is closed at t=0.

The rate at which the current through the inductor increases initially isView Solution

