Calculate the moment of inertia of a ring having mass M, radius Rand having uniform mass distribution about an axis passing through the centre of the ring and perpendicular to the plane of the ring?

For a continuous body, moment of inertia is given by
I=∫(dm)r2
Because each element is at equal distance from the axis,
so r=R:I=R2∫dm=MR2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.16videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
Find out the moment of inertia of the circular arcs shown, each having mass M, radius R and having uniform mass distribution about an axis passing through the centre and perpendicular to the plane ?
 View Solution
View Solution
Calculate the moments of inertia of the figures shown, each having mass M, radius R and having uniform mass distribution about an axis perpendicular to the plane and passing through the centre?View Solution
Knowledge Check
- Question 1 - Select One
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2 - Question 2 - Select One
From a circular ring of mass M and radius R, an arc corresponding to a 90∘ sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is k times MR2. Then the value of k is
A3/4B7/8C1/4D1/8 - Question 3 - Select One
From a complete ring of mass M and radius R, a 30∘sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,A912MR2B1112MR2C11.312MR2DMR2
,A912MR2B1112MR2C11.312MR2DMR2
Find the out the moment of inertia of a ring having uniform mass distribution of mass M and radius R about an axis which is tangent ot the ring and a in the plane of the ring b. perpendicular to the plane of the ring.
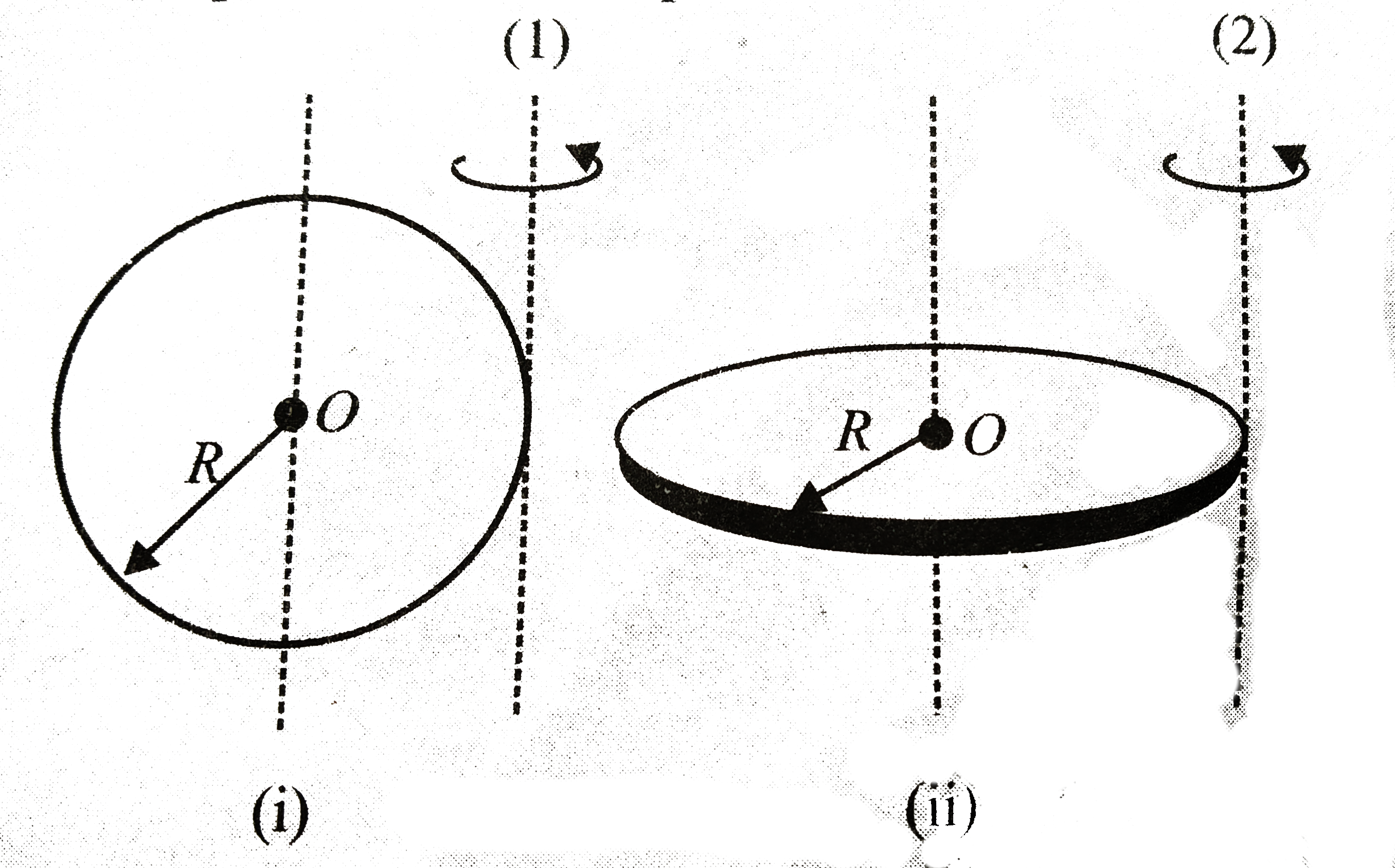 View Solution
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be
 View Solution
View SolutionThe moment of inertia of a flat angular ring having mass M, inner radius a and outer radius b about the diametric axis through the centre is
View SolutionFrom a circular ring of mass M and radius R, an arc corresponding to a 90∘ sector is removed. The moment of inertia of the ramaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is k times MR2. Then the value of k is
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be :-
 View Solution
View Solution

