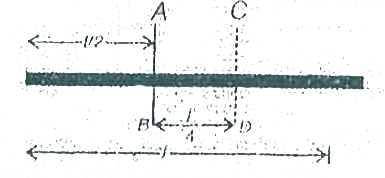Calculate the moment of inertia of each particle in Fig. about the indicated axis of rotation.

Video Solution

Text Solution

Verified by Experts

a. $I = m {(\frac{l}{2})}^{2} + m {(\frac{l}{2})}^{2} = \frac{m l^{2}}{2}$
b. $I = 4 m l^{2}$
c. $I = m l^{2} + m {(\frac{l}{2})}^{2} = \frac{5}{4} m l^{2}$
$d . I = 2 m {(2 l)}^{2} = 8 m l^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.3
15videos
RIGID BODY DYNAMICS 1
BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.4
11videos
RIGID BODY DYNAMICS 1
BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6videos
RIGID BODY DYNAMICS 1
BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2videos
PROPERTIES OF SOLIDS AND FLUIDS
BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2videos
RIGID BODY DYNAMICS 2

Similar Questions

Knowledge Check

Question 1 - Select One
Two bodies have their moments of inertia l and 2l respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular velocity will be in the ratio
A $2 : 1$
B $1 : 2$
C $\sqrt{2} : 1$
D $1 : \sqrt{2}$
Question 2 - Select One
Two bodies have their moments of inertia $I$ and $2 I$ respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio.
A $1 : 2$
B $\sqrt{2} : 1$
C $2 : 1$
D $1 : \sqrt{2}$
Question 3 - Select One
Two bodies have their moments of inertia $I$ and $2 I$ , respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular velocity will be in the ratio
A $2 : 1$
B $1 : 2$
C $\sqrt{2} : 1$
D $1 : \sqrt{2}$

CENGAGE PHYSICS-RIGID BODY DYNAMICS 1-Exercise 2.2

Home
Ask Doubt
Profile