Calculate the percentage increase in the moment of inertia about the axis of symmetry of a flywheel when the diameter of the flywheel is increased by 2%.
The correct Answer is:4%
To solve the problem of calculating the percentage increase in the moment of inertia of a flywheel when its diameter is increased by 2%, we can follow these steps:
1. Understand the Moment of Inertia Formula:
The moment of inertia I of a flywheel (assuming the mass is concentrated at the periphery) is given by the formula:
I=MR2
where M is the mass of the flywheel and R is the radius.
2. Differentiate the Moment of Inertia:
To find the change in moment of inertia, we differentiate I with respect to R:
dI=d(MR2)=M⋅d(R2)=M⋅(2R⋅dR)
Thus, we have:
dI=2MR⋅dR
3. Express the Change in Moment of Inertia:
We can express the relative change in moment of inertia as:
dII=dIMR2=2MR⋅dRMR2=2dRR
4. Relate Diameter Change to Radius Change:
Given that the diameter of the flywheel is increased by 2%, we can relate this to the radius. Since the diameter D=2R, an increase in diameter by 2% means:
dDD=0.02
Therefore, since D=2R:
dDD=dD2R=dRR
This implies:
dRR=0.022=0.01
5. Calculate the Percentage Increase in Moment of Inertia:
Now substituting dRR into the equation for the change in moment of inertia:
dII=2⋅dRR=2⋅0.01=0.02
To convert this into a percentage, we multiply by 100:
dII⋅100=0.02⋅100=2%
6. Final Calculation:
Therefore, the percentage increase in the moment of inertia when the diameter of the flywheel is increased by 2% is:
Percentage Increase=4%
Final Answer:
The percentage increase in the moment of inertia of the flywheel is 4%.
The moment of inertia I of a flywheel (assuming the mass is concentrated at the periphery) is given by the formula:
I=MR2
where M is the mass of the flywheel and R is the radius.
To find the change in moment of inertia, we differentiate I with respect to R:
dI=d(MR2)=M⋅d(R2)=M⋅(2R⋅dR)
Thus, we have:
dI=2MR⋅dR
We can express the relative change in moment of inertia as:
dII=dIMR2=2MR⋅dRMR2=2dRR
Given that the diameter of the flywheel is increased by 2%, we can relate this to the radius. Since the diameter D=2R, an increase in diameter by 2% means:
dDD=0.02
Therefore, since D=2R:
dDD=dD2R=dRR
This implies:
dRR=0.022=0.01
Now substituting dRR into the equation for the change in moment of inertia:
dII=2⋅dRR=2⋅0.01=0.02
To convert this into a percentage, we multiply by 100:
dII⋅100=0.02⋅100=2%
Therefore, the percentage increase in the moment of inertia when the diameter of the flywheel is increased by 2% is:
Percentage Increase=4%
The percentage increase in the moment of inertia of the flywheel is 4%.
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ANGULAR MOMENTUM - CONSERVATION)
14 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
24 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM CENTRE OF MASS)
8 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
Knowledge Check
The moment of inertia of a rod about its perpendicular bisector is I . When the temperature of the rod is increased by ΔT , the increase in the moment of inertia of the rod about the same axis is (Here , α is the coefficient of linear expansion of the rod )
AαIΔTB2αIΔTCαIΔT2D2IΔTα
Calculate the moment of inertia of a disc about its any diameter ?
View SolutionCalculate the moment of inertia of a disc about its any diameter ?
View SolutionCalculate the moment of inertia of the given rod about an axis CD.
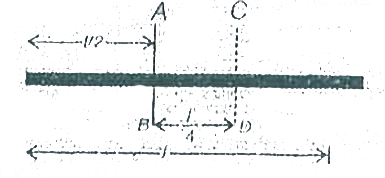
View SolutionDerive an expression for the moment of inertia of a thin spherical shell about a diameter.
View SolutionFor the structure shown in figure, moment of inertia about an axis passing through yy' is
_PHY_213_Q01.png)
View SolutionThe moment of inertia of a body about a given axis of rotation depends upon :-
View SolutionWhat is the moment of inertia of a circular disc about one of its diameters ?
View Solution