Calculate the smallest angular separation resolved by the human eye, given : aperature =2.5mm and effectived λ=5500.A. If a scale with mm markings is viewed by the unaided eye, deduce the largest distance to which the markings will be visible.
To solve the problem step by step, we will calculate the smallest angular separation resolved by the human eye and then deduce the largest distance at which the markings on a scale can be seen.
Step 1: Convert the given values to standard units
1. Wavelength (λ): Given as 5500 Å (angstroms).
- Convert to meters:
λ=5500Å=5500×10−10m=5.5×10−7m
2. Aperture (a): Given as 2.5 mm.
- Convert to meters:
a=2.5mm=2.5×10−3m
Step 2: Use the formula for angular resolution
The formula for the smallest angular separation (θ) that can be resolved by a circular aperture is given by:
θ=1.22λa
Substituting the values of λ and a:
θ=1.225.5×10−72.5×10−3
Step 3: Calculate the angular resolution
Now, we will perform the calculation:
θ=1.22×5.5×10−72.5×10−3=1.22×2.2×10−4=2.684×10−4radians
Rounding this, we get:
θ≈2.7×10−4radians
Step 4: Relate angular separation to distance
To find the largest distance (x) at which the markings on a scale can be seen, we use the relationship:
θ=1mmx
Where 1 mm is the separation between the markings. Rearranging gives:
x=1mmθ=1×10−32.7×10−4
Step 5: Calculate the distance x
Now, we will perform the calculation:
x=1×10−32.7×10−4≈3.70m
Conclusion
The largest distance at which the markings will be visible is approximately:
3.7m
1. Wavelength (λ): Given as 5500 Å (angstroms).
- Convert to meters:
λ=5500Å=5500×10−10m=5.5×10−7m
- Convert to meters:
a=2.5mm=2.5×10−3m
The formula for the smallest angular separation (θ) that can be resolved by a circular aperture is given by:
θ=1.22λa
Substituting the values of λ and a:
θ=1.225.5×10−72.5×10−3
Now, we will perform the calculation:
θ=1.22×5.5×10−72.5×10−3=1.22×2.2×10−4=2.684×10−4radians
Rounding this, we get:
θ≈2.7×10−4radians
To find the largest distance (x) at which the markings on a scale can be seen, we use the relationship:
θ=1mmx
Where 1 mm is the separation between the markings. Rearranging gives:
x=1mmθ=1×10−32.7×10−4
Now, we will perform the calculation:
x=1×10−32.7×10−4≈3.70m
The largest distance at which the markings will be visible is approximately:
3.7m
Topper's Solved these Questions
Similar Questions
Three mass points each of mass m are placed at the vertices of an equilateral triangle of side l. What is the gravitational field and potential at the centroid of the triangle due to the three masses?
View SolutionCalculate the least value of the angular separation of two stars which can be resolved by a telescope of 200 cm aperture. If the aperture of the human eye be 2mm and if the focal length of the eyepiece be 1 inch, what must be the minimum focal length of the objective if full resolving power of the telescope is to be utilized. Take λ=5500A0.
View SolutionA microscope has objective of aperture 8mm and focal length 2.5cm. Estimate its resolving power. Given λ=5500.A.
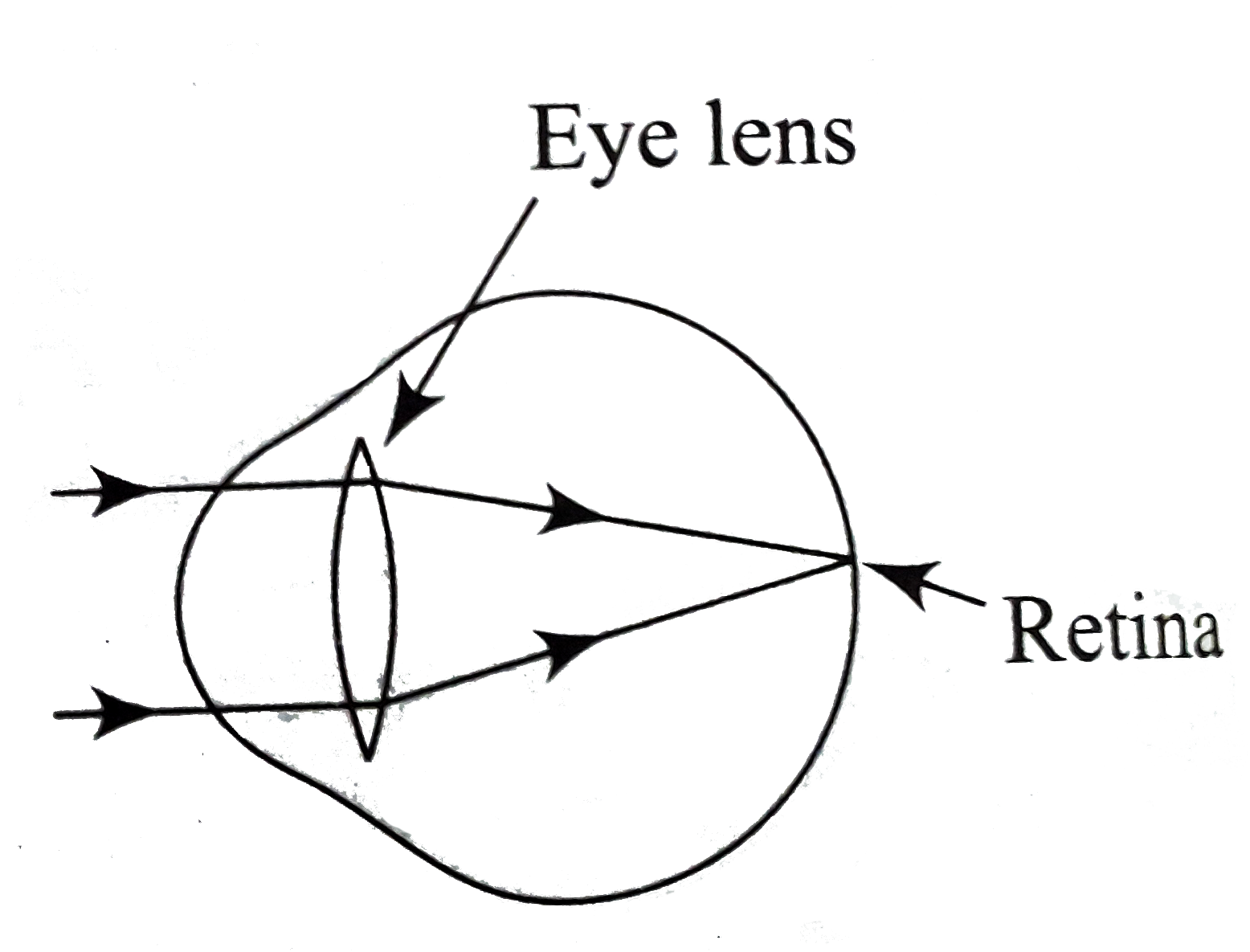
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
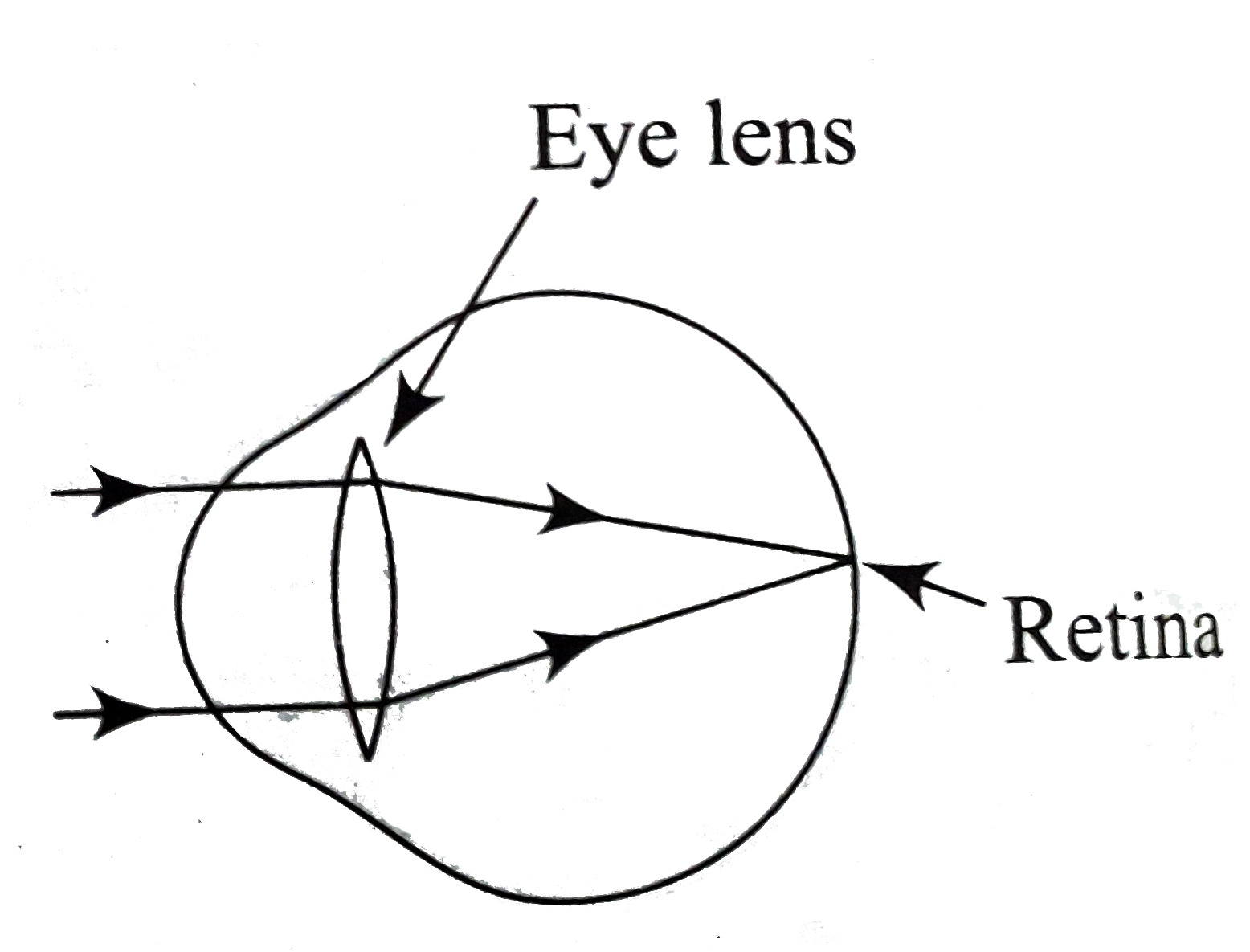
Q. Minimum focal length of eye lens of a normal peson is
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
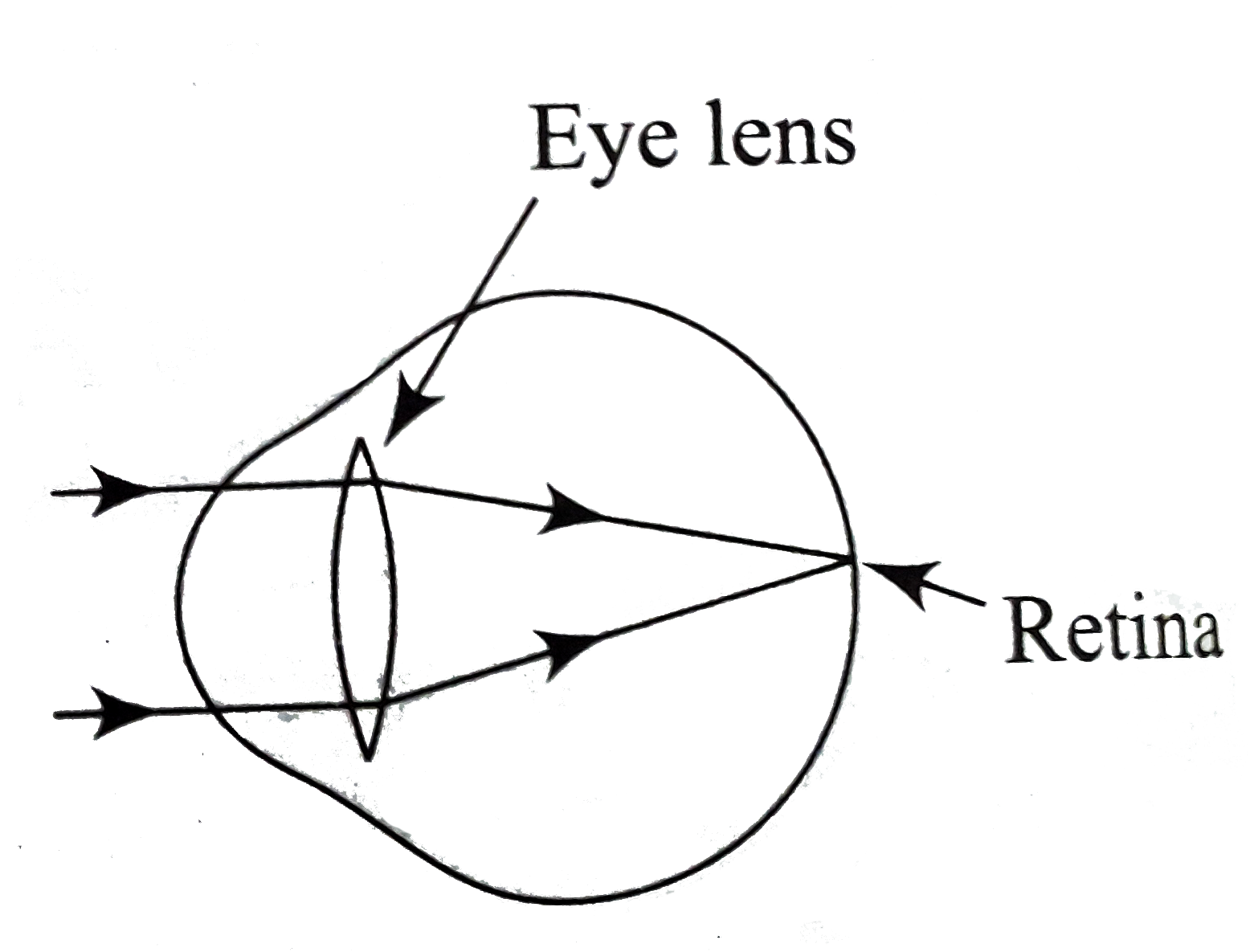
Q. Maximum focal length of a eye lens of a normal person is
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
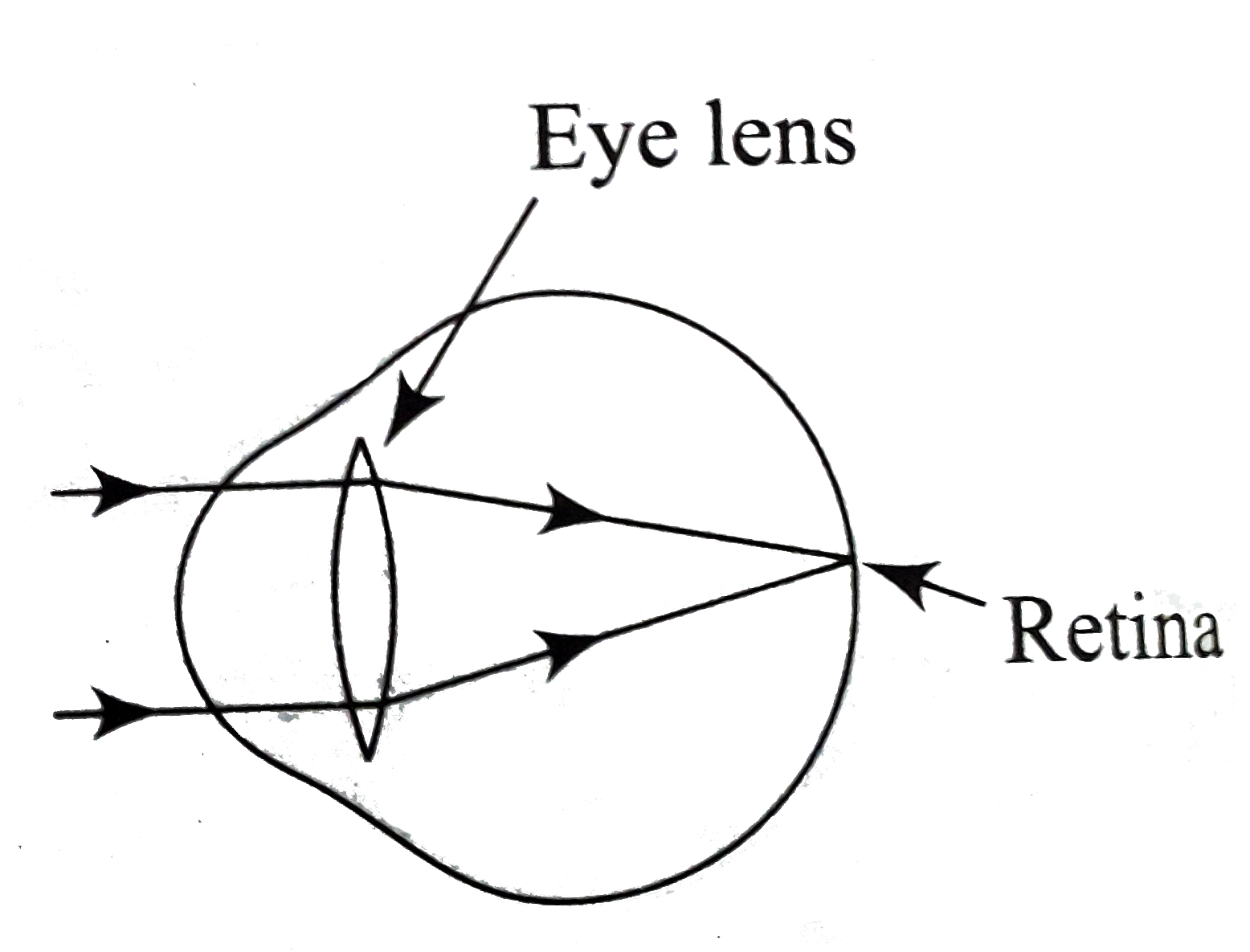
Q. A far sighted man connot see objects clearly unless they are at least 100cm from his eyes. The number of the spectacle lenses that will make his range of clear vision equal to an average grown up person will be
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
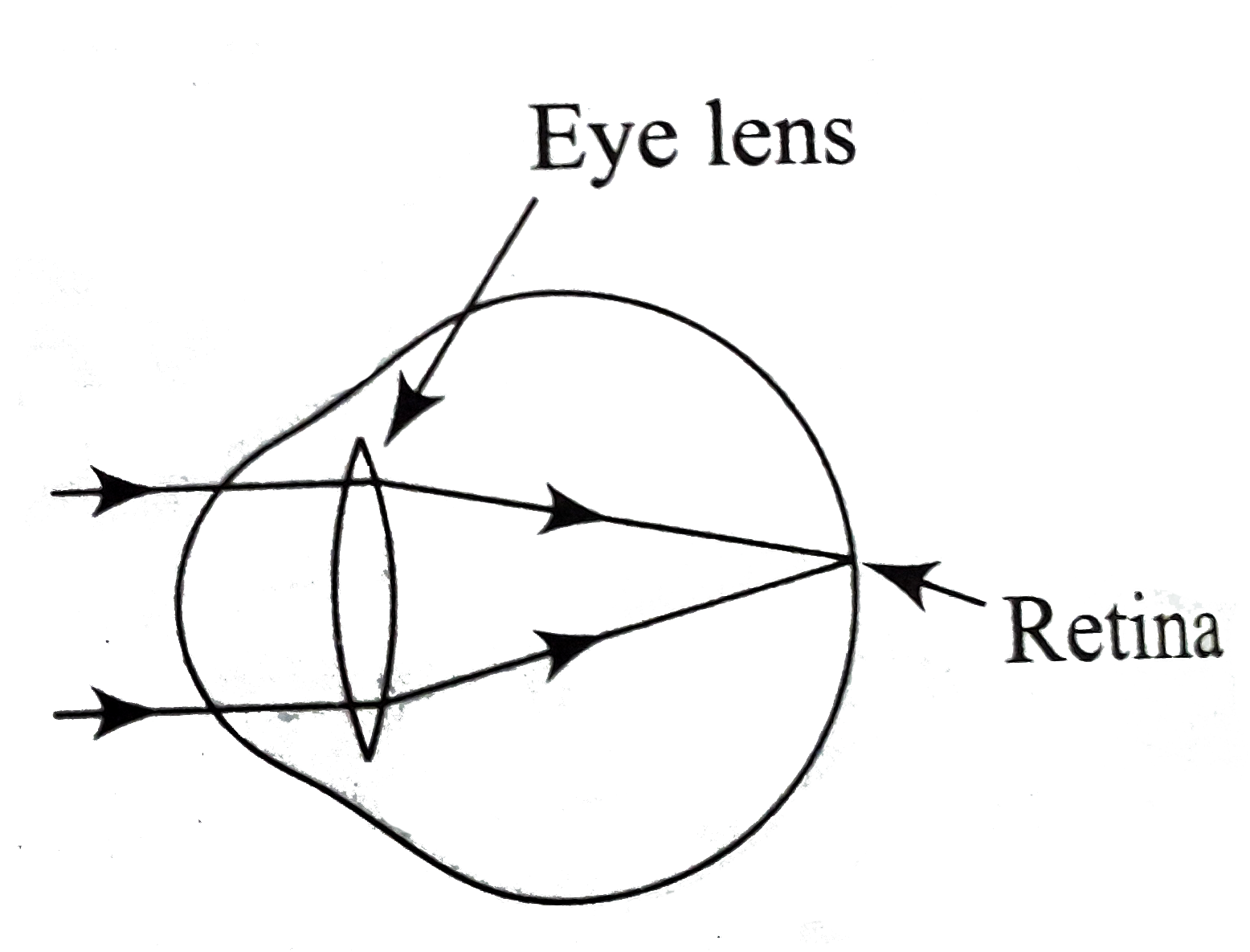
Q. A near sighted man can clearly see ojects only upto a distance of 100cm and not beyond this. The number of the spectacle lenses necessary for the remedy of this defect will be
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
Q. A person can see objects clearly from distance 10cm to ∞. Then, we can say that the person is
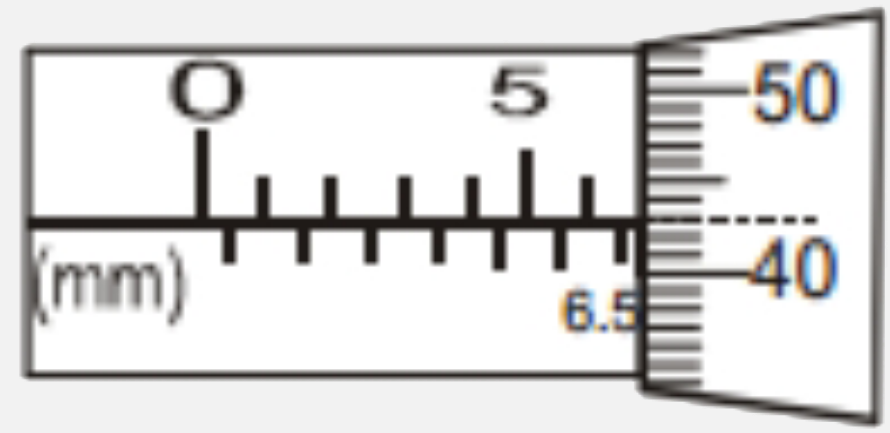
View SolutionThe figure shown below is a screwgauge. When the circular scale division matches the main scale at 43, the 6.5 mm mark on the main scale is just visible. The main scale has 12mm marks. In complete rotation, the screw advances by 12 mm and circular scale has 50 divisions. The reading of the screwgauge is
View SolutionA person with a normal near point (25cm) using a compound microscope with an objective of focal length 8.0mm and eye piece of focal length 2.5cm can bring an object placed 9.0cm from the objective in sharp focus. What is the separation between the two lenses ? Calculate the magnifying power of the microscope ?
View Solution
