Car A and car B start moving simultaneously in the same direction along the line joining them. Car A moves with a constant acceleration a=4m/s2, while car B moves with a constant velocity v=1m/s. At time t=0, car A is 10m behind car B. Find the time when car A overtake car B.
The correct Answer is:A
To solve the problem of when car A overtakes car B, we can follow these steps:
Step 1: Define the initial conditions
- Car A starts 10 meters behind car B.
- Car A has an initial velocity uA=0 m/s and accelerates at aA=4 m/s².
- Car B moves with a constant velocity vB=1 m/s and has an initial velocity uB=1 m/s.
Step 2: Write the equations of motion for both cars
1. For Car A (which has acceleration):
SA=uAt+12aAt2
Substituting the values:
SA=0⋅t+12⋅4⋅t2=2t2
2. For Car B (which has constant velocity):
SB=uBt+d0
Here, d0=10 m (the initial distance ahead of car A):
SB=1⋅t+10=t+10
Step 3: Set the distances equal to find when car A overtakes car B
To find when car A overtakes car B, we set SA=SB:
2t2=t+10
Step 4: Rearrange the equation
Rearranging gives us:
2t2−t−10=0
Step 5: Solve the quadratic equation
Using the quadratic formula t=−b±√b2−4ac2a:
- Here, a=2, b=−1, and c=−10.
- Calculate the discriminant:
D=b2−4ac=(−1)2−4⋅2⋅(−10)=1+80=81
- Now, apply the quadratic formula:
t=−(−1)±√812⋅2=1±94
This gives us two potential solutions:
1. t=104=2.5 seconds
2. t=−84=−2 seconds (not physically meaningful)
Step 6: Conclusion
Thus, car A overtakes car B after 2.5 seconds.
---
- Car A starts 10 meters behind car B.
- Car A has an initial velocity uA=0 m/s and accelerates at aA=4 m/s².
- Car B moves with a constant velocity vB=1 m/s and has an initial velocity uB=1 m/s.
1. For Car A (which has acceleration):
SA=uAt+12aAt2
Substituting the values:
SA=0⋅t+12⋅4⋅t2=2t2
SB=uBt+d0
Here, d0=10 m (the initial distance ahead of car A):
SB=1⋅t+10=t+10
To find when car A overtakes car B, we set SA=SB:
2t2=t+10
Rearranging gives us:
2t2−t−10=0
Using the quadratic formula t=−b±√b2−4ac2a:
- Here, a=2, b=−1, and c=−10.
- Calculate the discriminant:
D=b2−4ac=(−1)2−4⋅2⋅(−10)=1+80=81
- Now, apply the quadratic formula:
t=−(−1)±√812⋅2=1±94
This gives us two potential solutions:
1. t=104=2.5 seconds
2. t=−84=−2 seconds (not physically meaningful)
Thus, car A overtakes car B after 2.5 seconds.
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Example Type 1
1 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Example Type 2
1 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
Two cars A and B are moving on parallel roads in the same direction. Car A moves with constant velocity 30m/s and car B moves with constant acceleration 2.5m/s2 . At , car A is ahead of car B and car B is moving with 12m/s velocity . The distance travelled by car B until it overtakes car A is
View SolutionTwo cars a and B starts motion with a velocity of 10m/s and 20m/s respectively. Car a moves with a constant acceleration of 2.5m/s2 and car B have constant acceleration of 0.5m/s2 as shown in figure. Find when car A will over take car B. Dimension of car is negligible as compare to distance. Find the time after which car A over takes car B.
View SolutionTwo cars, A and B move along the x-axis. Car A starts from rest with constant accelertion while car B moves with consstant velocity.
a. At what time s, t s, if any, do A and B have the same position?
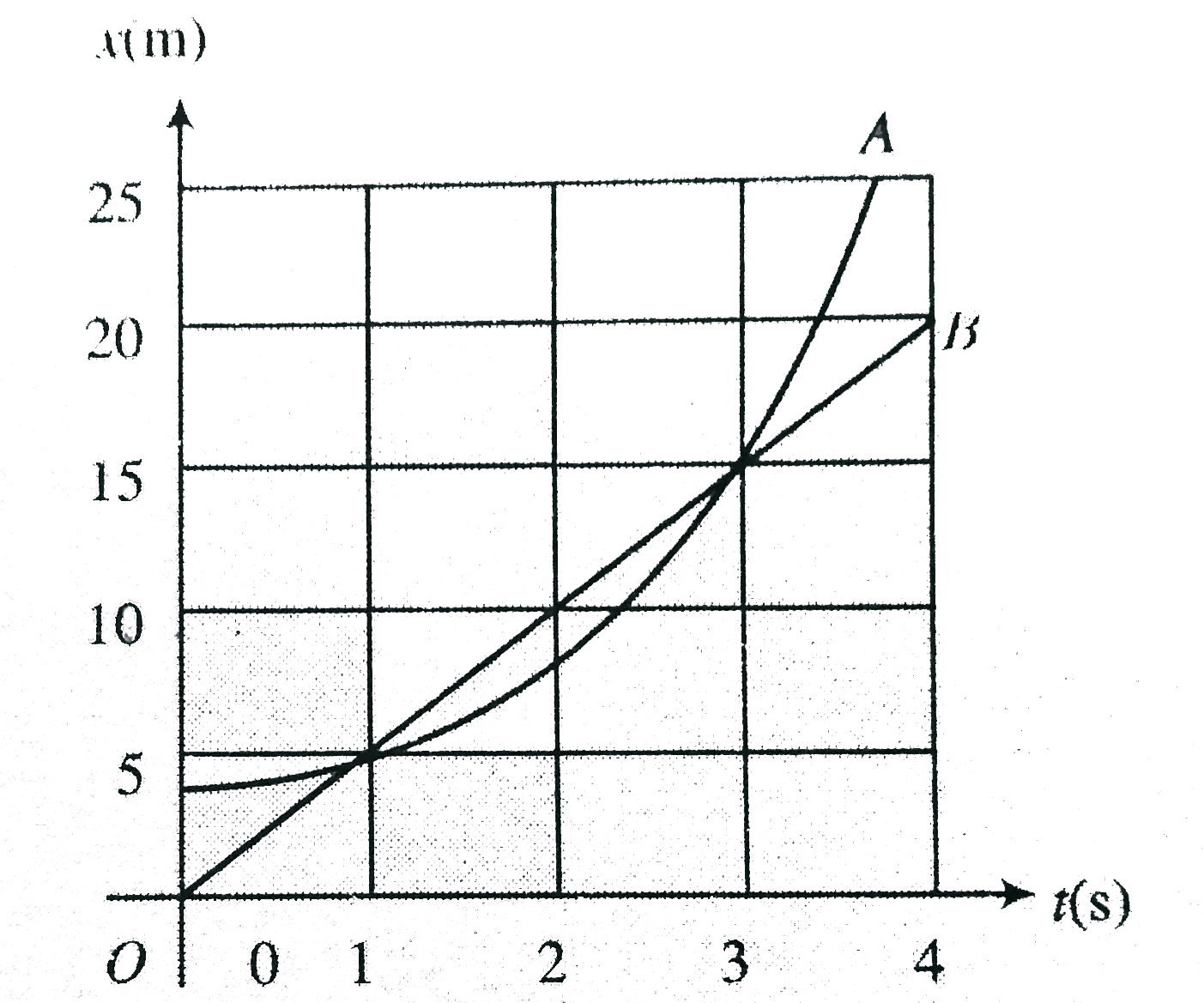 .
.
b. At what time s if any, do A and B have the same velocity? What is the velocity of car B at this time.
c. Graph velocity versus time for both A and B.
d. At what time s. If any, does car ApasscarA?<br>e.Atwˆtimes,ifanydoescarBpasscarA?
View SolutionA small sphere is suspended by a string from the ceiling of a car. If the car beings to move with a constant acceleration a, the inclination of the string to the vertical is:
View SolutionA car moving with constant acceleration crosses two points A and B with velocities 10 m/s and 20 m/s in its path. Find the velocity of the car midway between A and B. (in m/s).
View SolutionTwo cars A and B are at rest at same point initially. If A starts with uniform velocity of 40 m/sec and B starts in the same direction with constant acceleration of4m/s2,then B will catch A after :
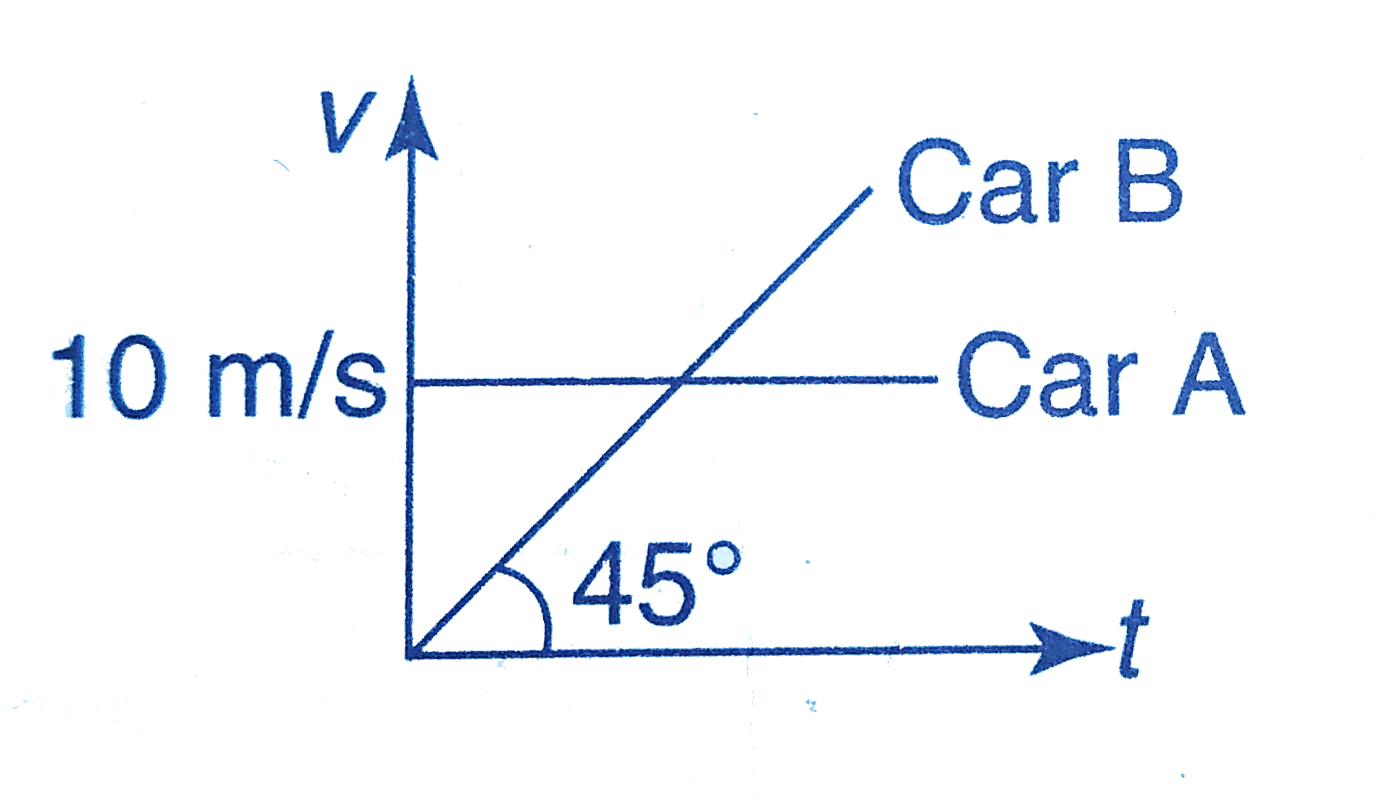
View SolutionInitially car A is 10.5m ahead of car B. Both start moving at time t=0 in the same direction along a straight line. The velocity-time graph of two cars is shown in figure. The time when the car B will catch the car A, will be.
View SolutionTwo cars move in the same direction along parallel roads. One of them is a 200m, long travelling with a velocity of 20m/s. The second one is 800m long travelling with a velocity of 7.5m/s. How long will it take for the first car to overtake the second car?
View SolutionTwo cars A and B start moving from the same point with same velocity v=5km/minute. Car A moves towards North and car B in moving towards East. What is the relative velocity of B with respect to A ?
View SolutionCar A has an acceleration of 2m/s2 due east and car B,4m/s2. due north. What is the acceleration of car B with respect to car A?
View Solution
