Certain weight is attached with a spring. It is pulled down and then released. It oscillates up and down. Its K.E. will be
maximum in the middle of the movement
maximum at the bottom
maximum just before it is released
constant
The correct Answer is:A
To determine where the kinetic energy (K.E.) of a weight attached to a spring is maximum during its oscillation, we can analyze the motion step by step.
1. Understanding the System:
- We have a spring attached to a fixed point, and a weight (mass) is hung from the free end of the spring. When the weight is pulled down and released, it will oscillate up and down due to the restoring force of the spring.
Hint: Visualize the spring's behavior when weight is applied and released.
2. Equilibrium Position:
- When the weight is attached, the spring stretches to a new equilibrium position due to the weight of the mass. At this position, the forces acting on the mass (weight and spring force) are balanced.
Hint: Remember that the equilibrium position is where the spring force equals the weight of the mass.
3. Displacement from Equilibrium:
- If the weight is pulled down further and then released, it will move upwards due to the spring force. As it moves, it will pass through the equilibrium position.
Hint: Consider the motion of the mass as it moves from the maximum displacement back to the equilibrium position.
4. Velocity and Kinetic Energy:
- At the maximum displacement (either up or down), the velocity of the mass is zero, which means the kinetic energy is also zero.
- As the mass moves towards the equilibrium position, it accelerates, and its velocity increases. The kinetic energy increases as the velocity increases.
Hint: Recall that kinetic energy is given by the formula K.E.=12mv2.
5. Maximum Kinetic Energy:
- The kinetic energy will be maximum when the mass passes through the equilibrium position because this is where the velocity is at its highest. After passing this point, the mass will start to decelerate as it moves towards the opposite extreme position.
Hint: Think about the relationship between velocity and kinetic energy; maximum velocity means maximum kinetic energy.
6. Conclusion:
- Therefore, the kinetic energy of the weight attached to the spring is maximum at the equilibrium position (the middle of the movement).
Final Answer: The kinetic energy will be maximum in the middle of the movement.
- We have a spring attached to a fixed point, and a weight (mass) is hung from the free end of the spring. When the weight is pulled down and released, it will oscillate up and down due to the restoring force of the spring.
- When the weight is attached, the spring stretches to a new equilibrium position due to the weight of the mass. At this position, the forces acting on the mass (weight and spring force) are balanced.
- If the weight is pulled down further and then released, it will move upwards due to the spring force. As it moves, it will pass through the equilibrium position.
- At the maximum displacement (either up or down), the velocity of the mass is zero, which means the kinetic energy is also zero.
- As the mass moves towards the equilibrium position, it accelerates, and its velocity increases. The kinetic energy increases as the velocity increases.
- The kinetic energy will be maximum when the mass passes through the equilibrium position because this is where the velocity is at its highest. After passing this point, the mass will start to decelerate as it moves towards the opposite extreme position.
- Therefore, the kinetic energy of the weight attached to the spring is maximum at the equilibrium position (the middle of the movement).
Topper's Solved these Questions
Similar Questions
When a body of mass 2.0 kg is suspended by a spring, the spring is stretched. If the body is pulled down slightly and released, it coscillated up and down. What force is applied on the body by the spring when it passes through the mean position ? (g=9.8Nkg−1)
View Solutioncorrect the following sentence
The old building has pulled down by them.
View Solution
Knowledge Check
A spring is hanging down from the ceiling, and an object of mass m is attached to the free end. The object is pulled down, thereby stretching the spring, and then released. The object oscillates up and down, and the time T required for one complete up-and-down oscillation is given by the equation T=2π√m/k, where k is known as the spring constant. What must be the dimension of k for this equation to be dimensionally correct?
A[M][T]B[T][M]C[M][T]2D[T][M]2Mass suspended to a spring is pulled down by 2.5 cm and let go. The mass oscillates with an amplitude of
A2.5 cmB5 cmC7.5 cmD10 cmA body of mass m is attached to the lower end of a spring whose upper end is fixed. The spring has negligible mass. When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1kg, the time period of oscillations becomes 5s. The value of m in kg is
A34B43C169D916
A block of mass 'm' is connected to the lower end of a massless vertically suspended spring. The ball is displaced slightly downward and released, it oscillates up and down. Match the coloum I and column II

View SolutionThe end of the rod which is connected to the spring is pushed down and released. Find time period of oscillation of the rod ?
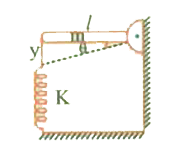
View SolutionA massless spring hangs from the ceiling with a small object attached to its lower end. The object is initially held at rest in a position y such that the spring is at its rest length. The object is then released from y and oscillates up and down, with its lowest position being 10cm below y, (a) What is the frequency of the oscillation? (b) What is the speed of the object when it is 8.0 cm below the initial position? (c ) An object of mass 600g is attached to the first object, after which the system oscillates with half the original frequency. What is the mass of the first object? (d) How far below y, is the new equilibrium (rest) position with both objects attached to the spring?
View SolutionOn suspending a heavy block of 2 kg from a massless spring, an extension of 5 cm is produced in the spring. If the block is further pulled down by 10 cm and then released then find the kinetic energy of oscillation of the spring.
View SolutionA body of mass m is attached to the lower end of a spring whose upper end is fixed. The spring has negligible mass. When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1kg, the time period of oscillations becomes 5s. The value of m in kg is
View Solution
