Choose the correct statements :
When the total area of the acceleration-time graph is negative, it always means that the final velocity of the particle is negative.
When the total area of the velocity-time graph is negative, it always means that the final displacement of the particle is negative.
When the total area of the velocity-time graph is negative, it may happen that the particle returns to its original position.
When the total area of the acceleration-time graph is negative, it may happen that the final velocity of the particle is zero .
The correct Answer is:C, D
To solve the problem of choosing the correct statements regarding the relationship between area under acceleration-time and velocity-time graphs, let's analyze each statement step by step.
1. Understanding the Concepts:
- The area under the acceleration-time graph represents the change in velocity (ΔV).
- The area under the velocity-time graph represents the change in displacement (Δx).
- If the area is positive, it indicates an increase in the respective quantity (velocity or displacement), while a negative area indicates a decrease.
2. Analyzing Statement A:
- Statement: "When the total area of the acceleration time graph is negative, it always means that the final velocity of the particle is zero."
- Analysis: This statement is incorrect. A negative area under the acceleration-time graph indicates a decrease in velocity, but it does not necessarily mean that the final velocity is zero. The final velocity could be negative or could remain positive, depending on the initial velocity.
3. Analyzing Statement B:
- Statement: "When the total area of the velocity time graph is negative, it always means that the final displacement of the particle is negative."
- Analysis: This statement is also incorrect. A negative area under the velocity-time graph indicates that the displacement has decreased, but it does not guarantee that the final displacement is negative. The final position could still be positive if the particle started from a sufficiently high positive position.
4. Analyzing Statement C:
- Statement: "When the total area of the velocity time graph is negative, it may happen that the particle returns to its original position."
- Analysis: This statement is correct. If the area is negative, it indicates that the particle has moved backward, but it could return to the original position if the backward movement is equal to the forward movement.
5. Analyzing Statement D:
- Statement: "When the total area of the acceleration time graph is negative, it may happen that the final velocity of the particle is zero."
- Analysis: This statement is correct. A negative area under the acceleration-time graph means that the velocity is decreasing, and it can reach zero if the initial velocity is sufficiently low.
Conclusion:
Based on the analysis:
- Correct Statements: C and D
- Incorrect Statements: A and B
- The area under the acceleration-time graph represents the change in velocity (ΔV).
- The area under the velocity-time graph represents the change in displacement (Δx).
- If the area is positive, it indicates an increase in the respective quantity (velocity or displacement), while a negative area indicates a decrease.
- Statement: "When the total area of the acceleration time graph is negative, it always means that the final velocity of the particle is zero."
- Analysis: This statement is incorrect. A negative area under the acceleration-time graph indicates a decrease in velocity, but it does not necessarily mean that the final velocity is zero. The final velocity could be negative or could remain positive, depending on the initial velocity.
- Statement: "When the total area of the velocity time graph is negative, it always means that the final displacement of the particle is negative."
- Analysis: This statement is also incorrect. A negative area under the velocity-time graph indicates that the displacement has decreased, but it does not guarantee that the final displacement is negative. The final position could still be positive if the particle started from a sufficiently high positive position.
- Statement: "When the total area of the velocity time graph is negative, it may happen that the particle returns to its original position."
- Analysis: This statement is correct. If the area is negative, it indicates that the particle has moved backward, but it could return to the original position if the backward movement is equal to the forward movement.
- Statement: "When the total area of the acceleration time graph is negative, it may happen that the final velocity of the particle is zero."
- Analysis: This statement is correct. A negative area under the acceleration-time graph means that the velocity is decreasing, and it can reach zero if the initial velocity is sufficiently low.
Based on the analysis:
- Correct Statements: C and D
- Incorrect Statements: A and B
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Linked Comprehension )15videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Matrix-Match)3videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Single Correct Choice Type)54videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Integer type )7videos
MAGNETIC FORCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)10videos
MOTION IN TWO AND THREE DIMENSIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Choose the correct statement(s) :
ABoth speed and velocity have the same units.BIf a body has a speed of 50ms−1 in a striaght line path , then its velocity is 180kmh−1CThe speed of a vechicle is measured by a device called speedometer.DAll the above - Question 2 - Select One
Choose the correct statement(s) :
ABeCO3 is kept in the atmosphere of CO2 since, it is least thermally stableBBe dissolves in alkali forming [Be(OH)4]2−CBeF4 forms complex ion with NaF in which Be goes with cationDBeF4 forms complex ion with NaF in which Be goes with anion - Question 3 - Select One
Choose the correct statement for the reaction
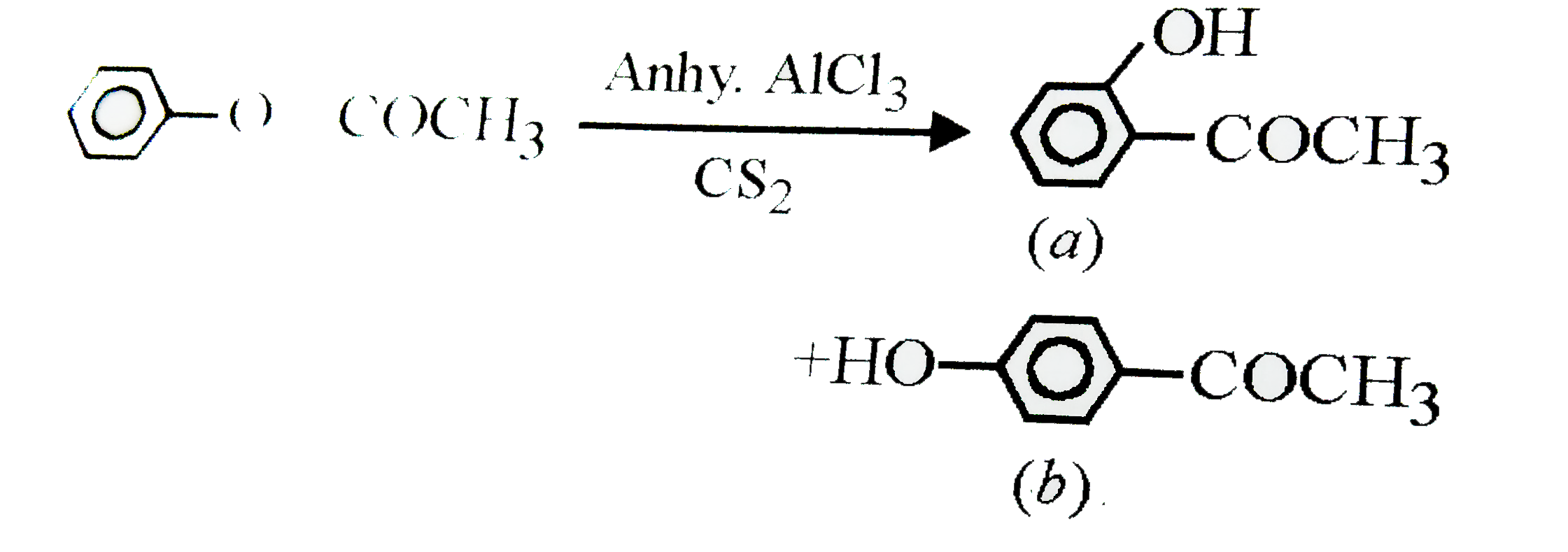 A(b) is formed more rapidly at higherB(b) is more volatile than (a)C(a) is more volatle than (b)D(a) is formed in higher yields at lower temperature
A(b) is formed more rapidly at higherB(b) is more volatile than (a)C(a) is more volatle than (b)D(a) is formed in higher yields at lower temperature

