The acceleration a of α of a particle depends on displacements covered in a time t as a=S+5 . It is given that initially S=0 m and v=5m/s. Then
v=S+5
v=√S+5
t=loge(S+5S)
t=loge(S+55)
The correct Answer is:A, D
To solve the problem, we need to derive expressions for velocity and time in terms of displacement S given the relationship between acceleration and displacement.
Step 1: Understand the relationship between acceleration, velocity, and displacement
We are given the equation for acceleration:
a=S+5
Acceleration can also be expressed in terms of velocity and displacement:
a=dvdt=vdvds
where v is the velocity and s is the displacement.
Step 2: Set up the equation
Substituting the expression for acceleration into the equation gives us:
vdvds=S+5
Rearranging this, we have:
vdv=(S+5)ds
Step 3: Integrate both sides
Now we will integrate both sides. The left side integrates with respect to v and the right side with respect to s:
∫vdv=∫(S+5)ds
This results in:
v22=S22+5S+C
where C is the constant of integration.
Step 4: Apply initial conditions
We know that initially S=0 and v=5 m/s. Plugging these values into the equation:
522=022+5(0)+C
This simplifies to:
252=C
So, the equation becomes:
v22=S22+5S+252
Step 5: Simplify the equation
Multiplying through by 2 to eliminate the fractions:
v2=S2+10S+25
This can be factored as:
v2=(S+5)2
Taking the square root gives us:
v=S+5
Step 6: Find the expression for time
Now we need to find the expression for time t in terms of displacement S. We know:
v=dsdt=S+5
Rearranging gives us:
dt=dsS+5
Step 7: Integrate to find time
Integrating both sides:
∫dt=∫dsS+5
This results in:
t=ln(S+5)−ln(5)+C′
Using the initial condition where S=0 at t=0:
0=ln(5)+C′⟹C′=−ln(5)
Thus, the equation for time becomes:
t=ln(S+55)
Final expressions
1. The expression for velocity in terms of displacement is:
v=S+5
2. The expression for time in terms of displacement is:
t=ln(S+55)
We are given the equation for acceleration:
a=S+5
Acceleration can also be expressed in terms of velocity and displacement:
a=dvdt=vdvds
where v is the velocity and s is the displacement.
Substituting the expression for acceleration into the equation gives us:
vdvds=S+5
Rearranging this, we have:
vdv=(S+5)ds
Now we will integrate both sides. The left side integrates with respect to v and the right side with respect to s:
∫vdv=∫(S+5)ds
This results in:
v22=S22+5S+C
where C is the constant of integration.
We know that initially S=0 and v=5 m/s. Plugging these values into the equation:
522=022+5(0)+C
This simplifies to:
252=C
So, the equation becomes:
v22=S22+5S+252
Multiplying through by 2 to eliminate the fractions:
v2=S2+10S+25
This can be factored as:
v2=(S+5)2
Taking the square root gives us:
v=S+5
Now we need to find the expression for time t in terms of displacement S. We know:
v=dsdt=S+5
Rearranging gives us:
dt=dsS+5
Integrating both sides:
∫dt=∫dsS+5
This results in:
t=ln(S+5)−ln(5)+C′
Using the initial condition where S=0 at t=0:
0=ln(5)+C′⟹C′=−ln(5)
Thus, the equation for time becomes:
t=ln(S+55)
1. The expression for velocity in terms of displacement is:
v=S+5
2. The expression for time in terms of displacement is:
t=ln(S+55)
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Linked Comprehension )15videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Matrix-Match)3videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Single Correct Choice Type)54videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Integer type )7videos
MAGNETIC FORCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)10videos
MOTION IN TWO AND THREE DIMENSIONS
Similar Questions
The acceleration of a particle which is depend on time is given by following function a = 2t + 1 and at time t = 0, x = 1m and ui = 2m/s. Then find out displacement of the particle at t = 3 sec.
View SolutionThe acceleration of a particle varies with time t as
a=t2+t+2
where t is in seconds.
The particle starts with an initial velocity v-3m/s at t=0. find the velocity of the particle at the end of 5s.View Solution
Knowledge Check
- Question 1 - Select One
The acceleration of a particle depends on displacement covered in a time as a=s+5. It is given that initially s=0 and v=5m/s, then which of the following is possibly correct ?
Av=s+5Bv=√s+5Cv=loge(s+55)2Dv=loge(s+5s) - Question 2 - Select One
The acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
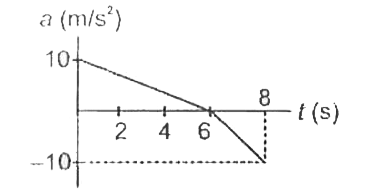 A+15m/sB+20m/sC−15m/sD−20m/s
A+15m/sB+20m/sC−15m/sD−20m/s
A particle having initial velocity u moves with a constant acceleration a for a time t. a. Find the displacement of the particle in the last 1 second . b. Evaluate it for u=5m/s,a=2m/s2andt=10s.
View SolutionIf a car accelerates with acceleration depend on displacement as a=6x2+2x+5. Find velocity of particles when it is at x=3m.Given that initially it starts from x=1 with velocity 2 m/s.
View SolutionThe acceleration of a particle is given by the relation as a=−kv5/2 , where is a constant. The particle starts at x=0 with a velocity of 16 m/s, and when x = 6, the velocity is observed to be 4 m/s. Find the velocity of particle when x=5m and the time at which the velocity ofthe particle is 9 m/s.
View SolutionThe displacement x of a particle is dependent on time t according to the relation : x=3−5t+2t2. If t is measured in seconds and s in metres, find its acceleration at t = 4s.
View SolutionThe acceleration of a particle is given by, a = t/6 at t = 0, velocity v = 2 m/s, displacement s= 2m. Find the velocity at t= 4 seconds,
View SolutionThe displacement s of a particle at a time t is given bys=t3−4t2−5t. Find its velocity and acceleration at t = 2.
View Solution

