Complete the following sentences:
(i) The S.I unit of moment of force is………
(ii) In equilibrium, algebraic sum of moments of all forces about all the point of rotation is ………
(iii) In a beam balance, when the beam is balanced in a horizontal position, it is in........... equilibrium.
(iv) the moon revolving around the earth is in....... equilibrium.
Let's solve the question step by step.
Step 1: Identify the S.I. unit of moment of force.
- The moment of force, also known as torque, is defined as the product of the force and the distance from the point of rotation (lever arm).
- The S.I. unit of force is Newton (N), and the distance is measured in meters (m).
- Therefore, the S.I. unit of moment of force is Newton meter (N·m).
Answer: The S.I. unit of moment of force is Newton meter.
Step 2: Understand the condition for equilibrium.
- In physics, when we talk about equilibrium, it means that the system is in a state where there is no net force or net moment acting on it.
- For a system to be in equilibrium, the algebraic sum of moments about any point of rotation must be zero.
- This means that all the clockwise moments must balance out the counterclockwise moments.
Answer: In equilibrium, the algebraic sum of moments of all forces about all points of rotation is 0.
Step 3: Identify the type of equilibrium in a beam balance.
- A beam balance is used to measure mass by comparing it to known weights.
- When the beam is balanced in a horizontal position, it indicates that the forces acting on it are balanced, and there is no net force or moment acting on it.
- This condition is referred to as static equilibrium, where the system is at rest.
Answer: In a beam balance, when the beam is balanced in a horizontal position, it is in static equilibrium.
Step 4: Determine the type of equilibrium of the moon revolving around the earth.
- The moon revolves around the earth due to the gravitational force acting as a centripetal force.
- Although it is in motion, the moon's motion is stable and uniform, meaning that it is not accelerating in the direction of its motion.
- This state is referred to as dynamic equilibrium, where an object is moving but the forces acting on it are balanced.
Answer: The moon revolving around the earth is in dynamic equilibrium.
Final Answers:
(i) The S.I unit of moment of force is Newton meter.
(ii) In equilibrium, the algebraic sum of moments of all forces about all points of rotation is 0.
(iii) In a beam balance, when the beam is balanced in a horizontal position, it is in static equilibrium.
(iv) The moon revolving around the earth is in dynamic equilibrium.
---
- The moment of force, also known as torque, is defined as the product of the force and the distance from the point of rotation (lever arm).
- The S.I. unit of force is Newton (N), and the distance is measured in meters (m).
- Therefore, the S.I. unit of moment of force is Newton meter (N·m).
- In physics, when we talk about equilibrium, it means that the system is in a state where there is no net force or net moment acting on it.
- For a system to be in equilibrium, the algebraic sum of moments about any point of rotation must be zero.
- This means that all the clockwise moments must balance out the counterclockwise moments.
- A beam balance is used to measure mass by comparing it to known weights.
- When the beam is balanced in a horizontal position, it indicates that the forces acting on it are balanced, and there is no net force or moment acting on it.
- This condition is referred to as static equilibrium, where the system is at rest.
- The moon revolves around the earth due to the gravitational force acting as a centripetal force.
- Although it is in motion, the moon's motion is stable and uniform, meaning that it is not accelerating in the direction of its motion.
- This state is referred to as dynamic equilibrium, where an object is moving but the forces acting on it are balanced.
(i) The S.I unit of moment of force is Newton meter.
(ii) In equilibrium, the algebraic sum of moments of all forces about all points of rotation is 0.
(iii) In a beam balance, when the beam is balanced in a horizontal position, it is in static equilibrium.
(iv) The moon revolving around the earth is in dynamic equilibrium.
Topper's Solved these Questions
- FORCE BOOK - ICSECHAPTER - FORCE EXERCISE - EXERCISE 1(A) Multiple choice questions
2 Videos
- FORCE BOOK - ICSECHAPTER - FORCE EXERCISE - EXERCISE 1(A) Numericals
18 Videos
- FORCE BOOK - ICSECHAPTER - FORCE EXERCISE - EXERCISE 1( C) Multiple Choice questions
2 Videos
- ELECTRO-MAGNETISM BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10 (C) NUMERICALS
1 Videos
- HOUSEHOLD CIRCUITS BOOK - ICSECHAPTER - HOUSEHOLD CIRCUITS EXERCISE - EXERCISE -9(B) (MULTIPLE CHOICE TYPE)
2 Videos
Similar Questions
In a beam balance, when the beam is balanced in horizontal position, it is in __________ equilibrium.
View SolutionComplete the following statements:(i) Probability of an event E + Probability of the event 'not E' =__.(ii) The probability of an event that cannot happen is___ Such an event is called__(iii) The probability of an event that is certain to happen is__. Such an event is called__.(iv) The sum of the probabilities of all the elementary events of an experiment is(v) The probability of an event is greater than or equal to __ and less than or equal to__
View Solution
Knowledge Check
Read the following statements and select the correct option.
(i) Increase in metained months after industrialisation in Great Britain is a proof for natural selection.
(ii) When more individuals of a population acquire a mean character value, it is called disruption.
(iii) Changes in allelic frequency in a population will lead to Hardy-Weinberg equilibrium.
(iv) Genetic drift changes the existing gene or allelic frequency in future generations.AOnly ii is correct.BOnly iv is correct.CBoth I and iv are correct.DBoth I and ii are correct.
A small circular coil with a mass of m consists of N turns of fine wire and carries a current of I. The coil is located in a uniform magnetic field of B with the coil axis orginally parallel to the field direction.

a. What is the period of small angle oscilations of the coil axis around its equilibrium position, assuming no friction and no mechanical force?
b. If the coil is rotated through an angle of θ from its equilibrium position and then released, what will be its angular speed when it passes through equilibrium position?
View SolutionConsider the situation shown in the diagram, where A small magnetised needle A is placed at a centre marked, as O. The direction of its mangetic moment I s indicated by arrow. The other arrow show different position (and orientations of the magnetic moment) of antoher identical magnetised eedle X.
In which configuration the system is not in equlibrium?
(ii) In which configuration is the system in (a) stable and (b) unsable equilibrium
(iii) Which configuration corresponds to the lowest potentials energy among all the configuration shown
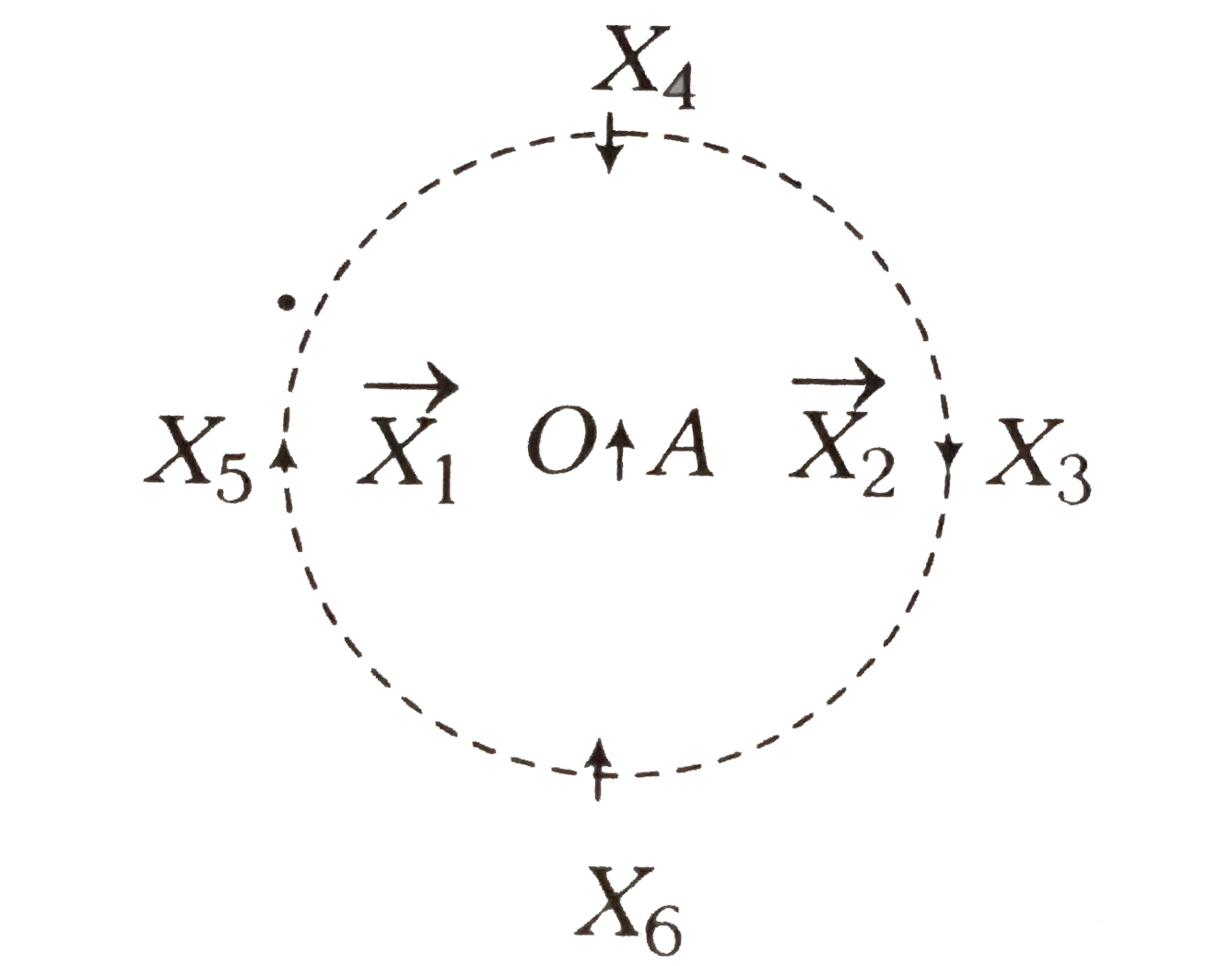
View SolutionFill in the blanks using appropriate word from the list at the end of each statement :
(i) The magnitude of accleration of a particle in S.H.M. is the ….. at the end points. (least, greatest)
(ii) The total energy of a particle in S.H.M. equals the ...... at the end point and the ..... at the mean position, (kinetic energy, potential energy)
(iii) the restoring force in S.H.M. is ........ in magnitude, when the particle is intantaneously at rest. (zero, maximum)
(iv) The time period of a particle in S.H.M. depends, in general , on ........, but in independent of ....... (amplitude, force constant, initial phase, mass, total energy).
(v) For a particle in S.H.M. with a given mass m and force constant k, quantities which depends on initial conditions are ...... (time period, amplitude, phase, total energy, frequency).
(vi) A particle in S.H.M. has ...... speed, and ..... magnitude of accleration at its mean position. (minimum, maximum)
View SolutionPotential energy function along x−axis in a certain force field is given as
U(x)=x44−2x2+112x2−6x
For the given force field :−
(i)the points of equilibrium are x=1, x=2 and x=3
(ii) the point x=2 is a point of unstable equilibrium.
(iii) the points x=1 and x=3 are points of stable equilibrium.
(iv) there exists no point of neutral equilibrium. The correct option is :−
View SolutionFigure shows a small magnetised needle P placed at a point O. The arrow shows the direction of magnetic moment. The other arrows show different positions (and orientations of the magnetic moment) of another identical magnetised needle Q.

(a) In which configuration is the system not in equilibrium?
(b) In which configuration is the system in (i) stable and (ii) unstable equilibrium?
(c) Which configuration corresponds to the lowest potential energy among all the configurations shown?
View SolutionWhich of the following examples represents (nearby) shm and which represents periodic but not shm.
(i) The rotation of earth about its axis.
(ii) Motion of an oscillating mercury column in a U-tube.
(iii) Motion of a ball bearing inside a smooth curved bowl when released from a point slightly above the lowermost position.
(iv) General vibration of a polyatomic molecules about its equilibrium configuration.
View SolutionRead the following paragraph and answer the questions given below ,
Stable equilibrium is of various types . Mechanical equilibrium is achieved when all particles are at rest and total potential energy of the system is minimum . At any stage where particles are at rest but the system is not at stable equilibrium as it can reduce its potential energy by reverting to another position, is called metastable equilibrium . Thermal equilibrium is result from the absence of temperature gradients in the system. Chemical equilibrium is obtained when no further reaction occurs between reacting substances, i.e forward and reverse rates of reaction are equal.
When steam with solid iron at high temperature Fe3O4(s) and hydrogen gas are produced . But the reaction never goes to completion. This is because as the products are formed the reaction proceeds in reverse direction and when rate of reverse reaction is equal to rate of forward reaction , the concentration of reactants and products become constant and equilibrium is reached.
The primary objective of the passage is
View Solution
