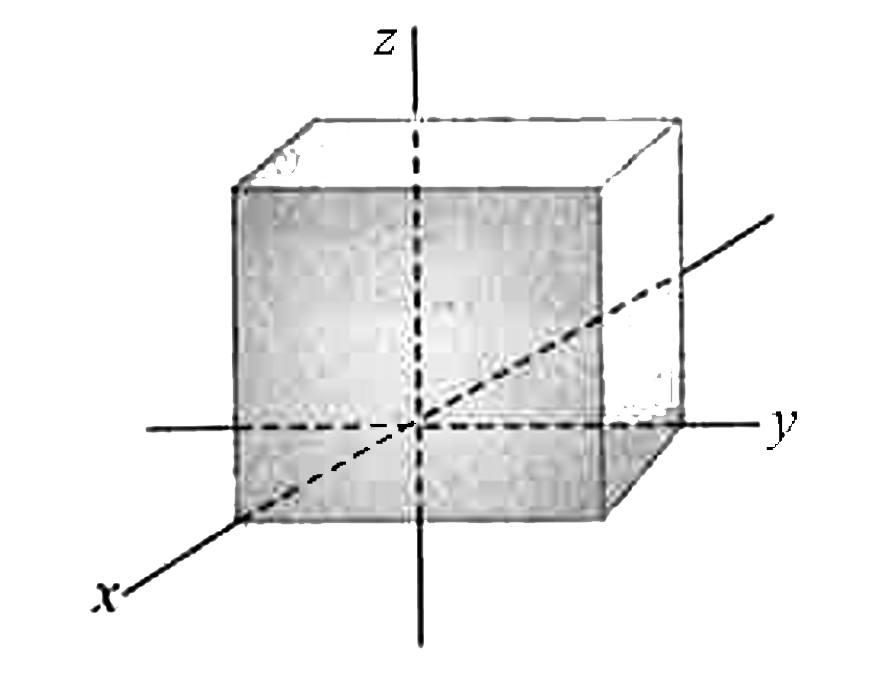
Conisder an electric field →E=E0ˆx where E0 is a constant .
The flux through the shaded area (as shown in the figure) due to this field is
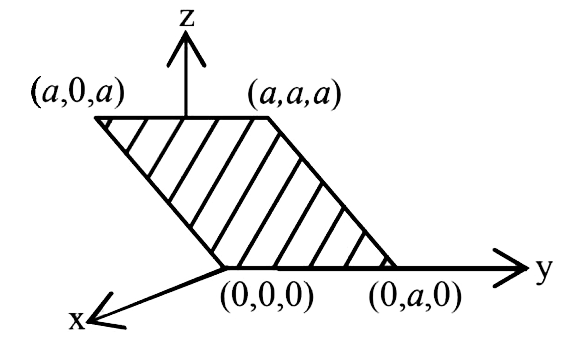
2E0a2
√2E0a2
E0a2
E0a2√2
The correct Answer is:C
Step by step video & image solution for Conisder an electric field vecE=E_0hatx where E_0 is a constant . The flux through the shaded area (as shown in the figure) due to this field is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GAUSS' LAW BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
2 Videos
- GAUSS' LAW BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)
6 Videos
- GAUSS' LAW BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PROBLEMS
42 Videos
- FORCE AND MOTION-IIBOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
1 Videos
- GEOMETRICAL OPTICS : REFLECTION BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
Similar Questions
Knowledge Check
If →E=E0Xaˆi(x−mt) then flux through the shaded area is:
 AE0a2BZeroCE0a3D−E0a3
AE0a2BZeroCE0a3D−E0a3If unifrom electric filed →E=E0ˆi+2E0ˆj, where E0 is a constant, exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,0) will be.
AzeroB−E0x0C−2E0x0D−√5E0x0If uniform electric field →E=E0ˆi+2E0ˆj, where E0 is a constant exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,2x0) will be -
AzeroB−5E0x0C−3E0x0D−√5E0x0
Find the area of the shaded field shown in the given figure

View SolutionFind the area of the shaded field shown in the given figure.
View SolutionA uniform electric field →E=aˆi+bˆj intersects a surface of area A .What is the flux through this area if the surface lies in the yz plane?
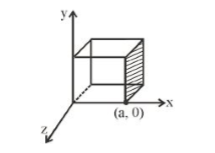
View SolutionGiven the components of an electric field as Ex=αx,Ey=0 and Ez=0, where α is a dimensional constant. Calculate the flux through each face of the cube of side a, as shown in the figure.

View SolutionAn electric field given →E=4.0ˆi−3.0(y2+2.0)j pierces a Gaussian cube of edge length 2.0 m and positioned as shown in the figure. (The magnitude E is in newtons per coulomb and the position z is in meters.) what is the electric flux through the (a) top face, (b) bottom face, (c) left face , (b) bottom facem (c) left face, and (d) back face ? (e) what is the net electric flux through the cube ?
View Solution