Consider a collection of a large number of particles each with speed v in a plane.The direction of velocity is randomly distributed in the collection.The magnitude of the average relative velocity of a particle with velocities of all other particles is
4v/π
3v/2π
5v/3π
2v/3π
The correct Answer is:A
Let →v1 and →v2 are the velocities of any two particles and θ is the angle between them. As each particle has same speed , so v1=v2=v
The relative velocity of particle 2 w.r.t. 1 is given by
→v21=→v2−→v1
or v21=√v2+v2−2vvcosθ=√2v2(1−cosθ)
=√2v2×2sin2θ/2=2vsinθ2
As the velocities of the particles are randomly distributed, so θ varies from 0 to 2π . The magnitude of average velocity when averaged over all such pairs . Thus
v21=∫2π0v21dθ∫2π0dθ=4vπ

Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Exercise -1 : CONCEPT BUILDER (TOPICWISE)60videos
MOTION IN A PLANE
- BOOK - DISHA PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-2 CONCEPT APPLICATOR24videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise-230videos
MOTION IN A STRAIGHT LINE
Similar Questions
Consider a collection of a large number of particles each with speed v. The direction of velocity is randomly distributed in the collection. Show that the magnitude of the relative velocity between a pair of particles averaged over all the pairs in the collection is greater than v.
View SolutionHow does particle velocity differ from wave velocity?
View Solution
Knowledge Check
- Question 1 - Select One
A large number of particles are moving each with speed v having directions of motion randomly distributed. What is the average relative velocity between any two particles averaged over all the pairs?
AvB(π/4)vC(4/π)vDZero - Question 2 - Select One
Average velocity of the particle for the motion
A3.3 m/sB6.7 m/sC2.7 m/sD7.6 m/s - Question 3 - Select One
In the pervious question ,what is the average velocity of the particle?
A1ms−1B0.5ms−1C3ms−1DNone of these
A particle is doing uniform circular motion as shown. Magnitude of average velocity of the particle between points A and C will be
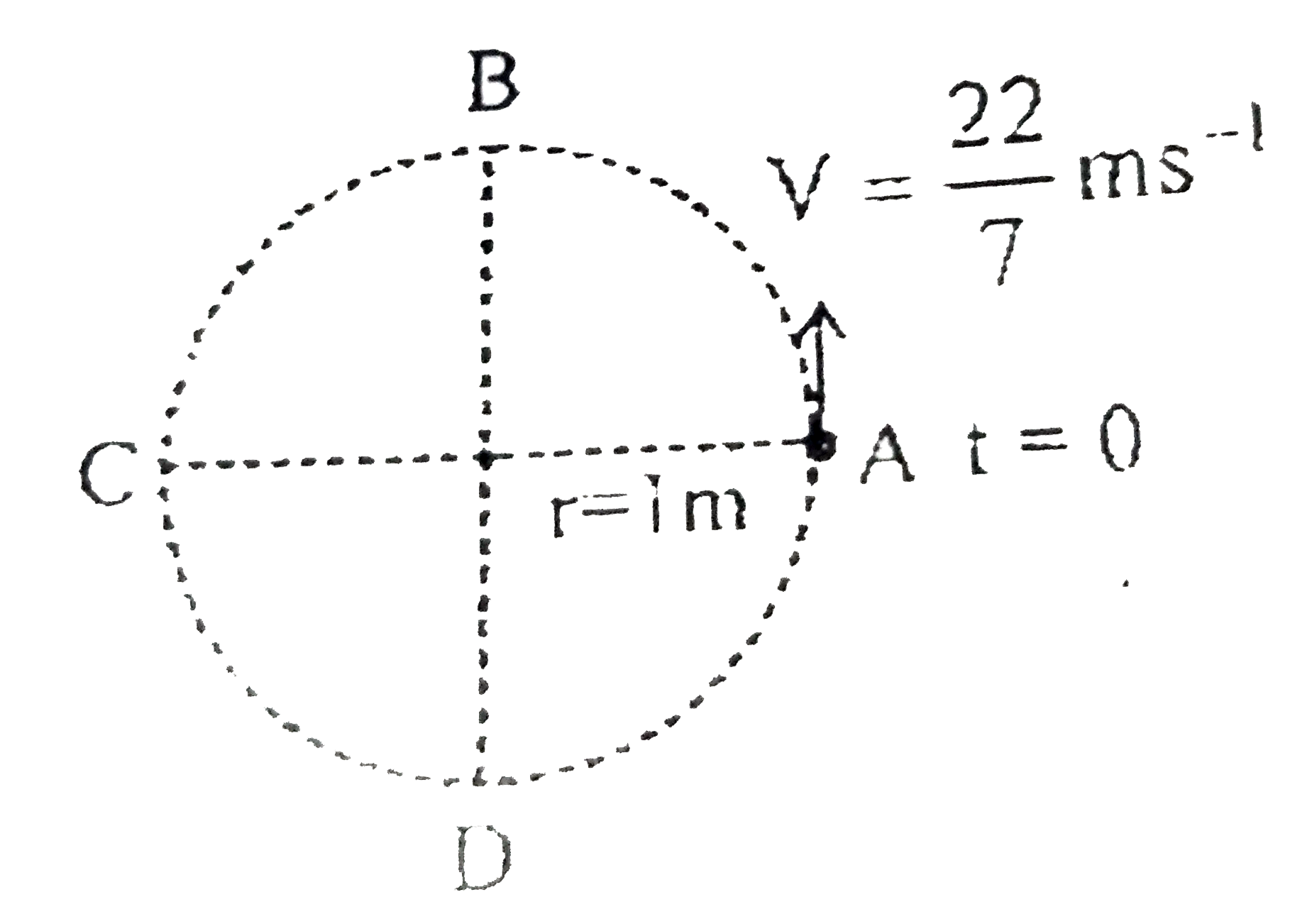 View Solution
View SolutionIn Q.36, average velocity during the motion of the particle is.
View SolutionThe magnitude of average velocity is equal to the average speed when a particle moves:-
View SolutionA particle is moving with a constant speed v in a circle. What is the magnitude of average velocity after half rotation?
View SolutionIn the previous question, the magnitude of velocity of particle at the mentioned instant is
View Solution

