A stone must be projected horizontally from a point P, which is h metre above the foot of a plane inclined at an angle θ with horizontal as shown in figure. What is the velocity v of the stone so that it may hit the inclined plane perpendicularly?

√2gh/(2+cot2θ)
√2ghcot2θ
√2gh/(1+tan2θ)
√2ghtan2θ
The correct Answer is:A
Take O as the origin and coordinates of point at which stone hits the plane are (x,y) . The velocity component along the plane v cosθ and perpendicular to it is v sinθ. As stone hit the plane perpendicularly, its velocity component v cos θ becomes zero. Let t is the time in which it becomes zero, then
0=vcosθ−gsinθt
which gives, t=vcosθgsinθ=vgcotθ...(i)
The vertical distance falls be stone in this time t
h−y=0+12gt2 ...(ii)
and x= v t ...(iii)
Also yx=tanθ⇒ or y=x tan θ=v t tan θ ...(iv)
Substituting values of t and y in equation (ii), we get
h−vttanθ=12gt2
or h−v(vgcotθ)tanθ=12g(vgcotθ)2
or h−v2g=v22gcot2θ⇒v=√2gh2+cot2θ
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Exercise -1 : CONCEPT BUILDER (TOPICWISE)
60 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - DISHA PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-2 CONCEPT APPLICATOR
24 Videos
- MOTION IN A STRAIGHT LINEBOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise-2
30 Videos
Similar Questions
A stone must be projected horizontally from a point P, which is h meter above the foot of a plane inclined at an angle θ with horizontal as shown in figure . Calculate the velocity v of the stone so that in may hit the incline plane perpendiculary.

View SolutionA particles is projected horizontally with a speed v from the top of a plane inclined at an angle tehta to the horizontal as shown in the figure.
(a) Hwo far from the point of projection will the particle strike the plane ?
(b) Find the time taken by the particel to hit the plane.
(c) What is the velocity of particle just before it hits the plane ?
View Solution
Knowledge Check
A particle is to be projected horizontally with velocity v from a point P, which is 60m above the foot of a plane inclined at angle 45∘ with horizontal as shown in figure. The particle hits the plane perpendicularly at A. After rebound from inlined plane it again hits at B. If coefficient of restitution between particles and plane is 1√2 then,
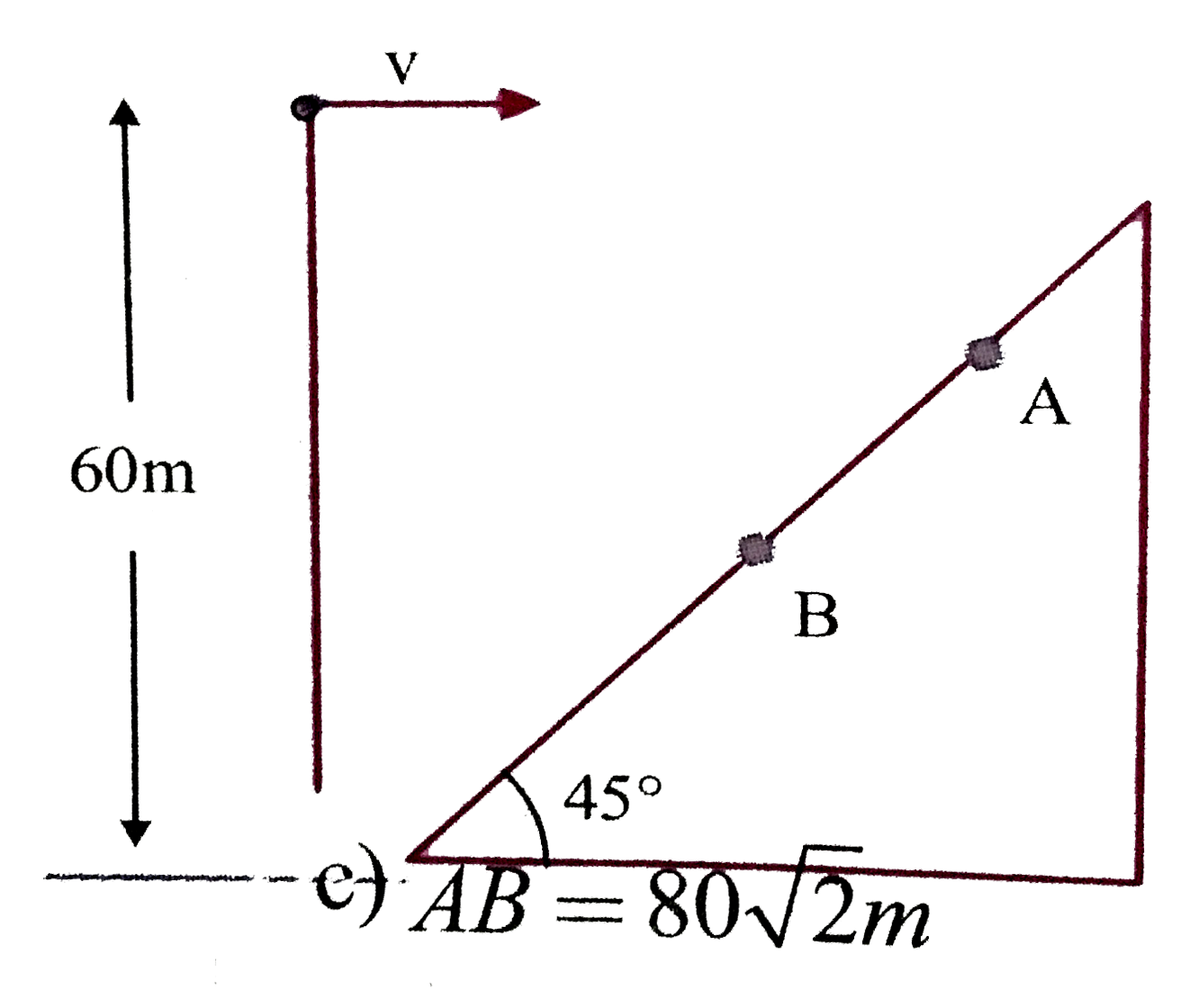 Av=20m/sBv=10m/sCAB=80√2mDAB=80m
Av=20m/sBv=10m/sCAB=80√2mDAB=80mA particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle θ=37∘ to the horizontal (g=10m/s2)

What is the velocity of the particle just before it hits the plane?A5√3m/sB52√13m/sC10√13m/sD5√26m/s
A particles is projected horizontally with a speed v from the top of a plane inclined at an angle tehta to the horizontal as shown in the figure.
(a) Hwo far from the point of projection will the particle strike the plane ?
(b) Find the time taken by the particel to hit the plane.
(c) What is the velocity of particle just before it hits the plane ?
View SolutionIn figure, find the horizontal velocity u(∈ms−1) of a projectile so that it hits the inclined plane perpendicularly. Given H=6.25m.

View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionDetermine the horizontal velocity v0 with which a stone must be projected horizontally from a point P, so that it may hit the inclined plane perpendicularly. The inclination of the plane with the horizontal is θ and point P is at a height h above the foot of the incline, as shown in the figure.
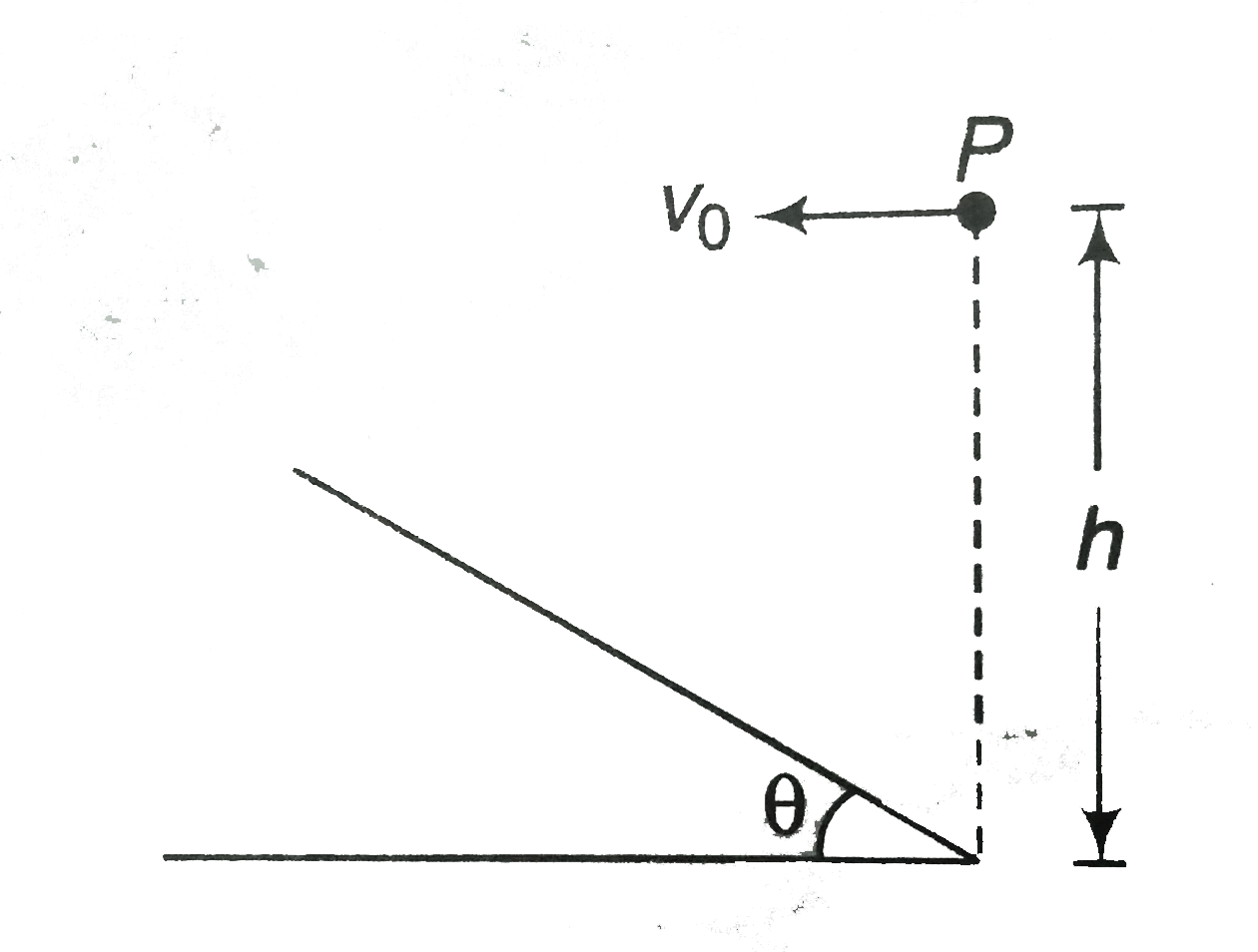
View SolutionDetermine the horizontal velocity v0 with which a stone must be projected horizontally from a point P, so that it may hit the inclined plane perpendicularly. The inclination of the plane with the horizontal is θ and point P is at a height h above the foot of the incline, as shown in the figure.

View Solution
