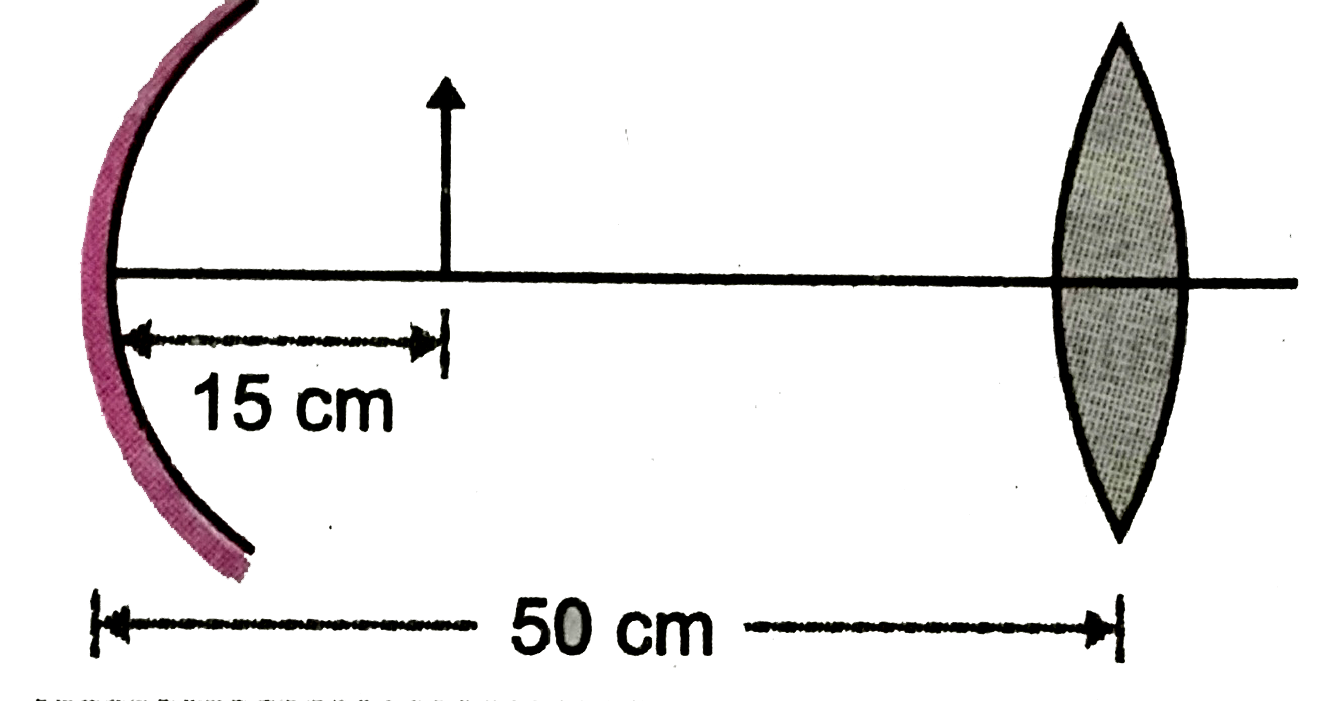
Consider a concave mirror and a convex lens (refractive index 1.5) of focal length 10cm each separated by a distance of 50cm in air (refractive index = 1) as shown in the Fig. An object is placed at a distance of 15cm from the mirror. Its erect image formed by this combination has magnification M1. When this set up is kept in a medium of refractive index 7/6, the magnification becomes M2. The magnitude (M2M1) is :
 .
.

Applying mirror formula
1v+1u=1f
1v=1f−1u=1−10+115
1v=−15+10150=−5150=−130
∵ v=−30cm
For convex lens u=|2fl|
Therefore image will have a magnification of l. when the set-up is kept in a medium The focal length of the lens will change
1fl1fl)))=(((n_l)/(n_s)-1))/(((n_l)/(n_s^())−1))⇒(fl))/(10)=[[(1.5)/(1)-1]]/([1.5/((7)/(6))-1])<br>impliesf_l^=17.5cm
Applying lens formula 1v−1u=1fl)<br>(1)/(v)-(1)/(-20)=(1)/(17.5)impliesv=15=40cm<br>M_l^=Magnificationby≤ns=(v)/(u)=(140)/(-20)=-7<br>Now[[M_2)/(M_1)]=|(MmirrorxxM_l^)Mmirror×Ml∣=7
Topper's Solved these Questions
Similar Questions
A concave mirror has a focal length of 5 cm. When an object is placed at a distance of 15 cm from the mirror, then the image is formed in front of the mirror at ____cm.
View SolutionA thin lens of refractive index 1.5 has focal length of 15cm in air. When the lens is placed is a medium of refractive index (4)/(3), its focal length will become …..cm.
View Solution
Knowledge Check
An object is placed at a distance of 15 cm from a concave mirror and its real image is formed at 30 cm in front of that mirror. The focal length of the mirror is
A+20 cmB−20 cmC−10 cmD+10 cmFocal length of a convex lens of refractive index 1.5 is 2 cm. Focal length of lens when immersed in a liquid of refractive index 1.25 will be
A10cmB2.5cmC5cmD7.5cmThe focal length of a convex lens of glass of refractive index 1.5 is 2 cm. The focal length of the lens when immersed in a liquid of refractive index 1.25 will be:
A2.5 cmB5 cmC1 cmD4 cm
A double convex lens made of glass of refractive index 1.56 has both radii of curvature of magnitude 20cm. If an object is placed at a distance of 10cm from this lens, find the position of image formed.
View SolutionA convex lens of refractive index 1.5 has a focal length of 20 cm in air. Calculate the change in its focal length when it is immersed in water of refractive index 4/3.
View SolutionA convex lens of refractive index 1.5 has a focal length of 18 cm in air. Calculate the change in its focal length when it is immersed in water of refraction index 43.
View SolutionA thin convex lens of refractive index 1.5cm has 20cm focal length in air. If the lens in completely immersed in a liquid of refractive index. 1.6, then its focal length will be
View SolutionAn image is formed at a distance of 100 cm from the glass surface with refractive index 1.5, when a point object is placed in the air at a distance of 100 cm from the glass surface. The radius of curvature is of the surface is
View Solution
