Consider a hollow sphere rolling with slipping with velocities as shown. Find the translational velocity after the hollow sphere starts pure rolling.
(a) 
(b) 
(c ) 
(a) Since v0>Rω0, hence the velocity of hollow sphere at A is not zero, i.e. impure rolling. After some time the body will start pure rolling so that vc.m.=Rω. For this linear velocity should decrease and angular velocity should increase. Therefore, friction will act in the backward direction, it will provide linear retardation and angular acceleration. Let vc.m.=v, when the body starts pure rolling.
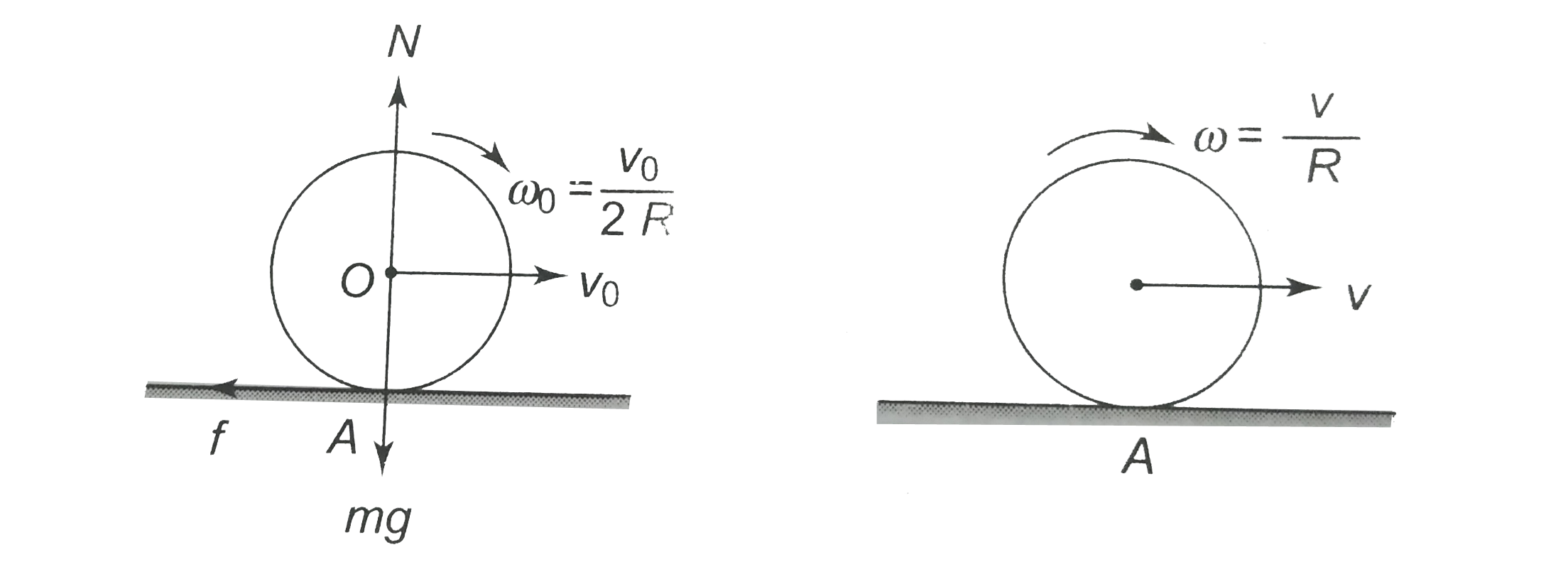
Since all forces passing through A, hence torque about A is zero, hence by the conservation of angular momentum about A.
mv0R+Ic.mω0=mvR+Ic.m.ω
mv0R+23mR2v02R=mvR+23mR2vR
43mv0R=53mvR⇒v=4v05
(b) 43mv0R−23mR2v02R=53mvR
23mv0R=53mvR⇒v=2v05
(c) mv02R+23mR2v0R=53mvR
v=7v010
Topper's Solved these Questions
Similar Questions
A sphere of mass M and radius r shown in figure slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre v02r. Find the translational velocity after the sphere starts pure rolling.
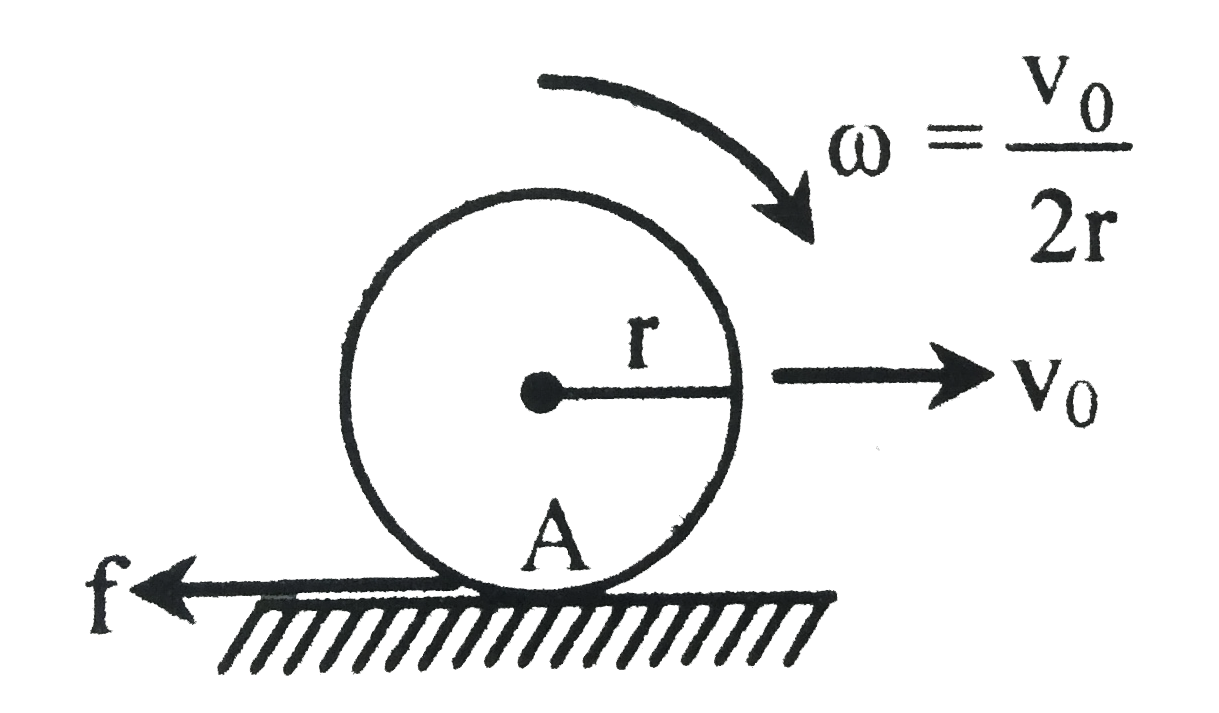 .View Solution
.View SolutionA solid sphere of mass M and radius r slips on a rough horizontal plane. At some instant it has translational velocity v0androtationalvelocityaboutthecentrev_(0) / 2 r.Thetranslationalvelocityafterthesphere⋆tspureroll∈gis(x v_(0))/(y)∈forwarddirection.F∈d(x+y).
'(##CEN_KSR_PHY_JEE_C09_E01_027_Q14##)'View Solution
Knowledge Check
- Question 1 - Select One
When a sphere rolls without slipping the ratio of its kinetic energy of translation to its total kinetic energy is.
A1:7B1:2C1:1D5:7 - Question 2 - Select One
If a solid sphere of mass 500 gram rolls without slipping with a velocity of 20 cm/s, then the rolling kinetic energy of the sphere will be
A140 JB280 JC0.014 JD0.028 J - Question 3 - Select One
Sphere in pure accelerated rolling
 AThe direction of fs is upwardsBThe direction of fs is downwardsCThe direction of gravitational force Is upwardsDThe direction of normal reaction Is downwards
AThe direction of fs is upwardsBThe direction of fs is downwardsCThe direction of gravitational force Is upwardsDThe direction of normal reaction Is downwards
A sphere of mass M and radius r shown in figure slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre v02r. Find the translational velocity after the sphere starts pure rolling.
 .View Solution
.View SolutionA hollow sphere is rolling without slipping on a rough surface. The ratio of translational kinetic energy to rotational kinetic energy is
View SolutionA hollow sphere starts pure rolling from rest as shown. The acceleration of centre of mass of sphere is
View SolutionA solid sphere rolls without slipping down a 30∘ inclined plane. If g=10ms−2 then the acceleration of the rolling sphere is
View SolutionA hollow sphere rolls without slipping down a plane inclined at an angle of 30° to the horizontal. Its linear acceleration will be
View Solution

